Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Полярное разложение
|
|
Напомним, что линейный оператор называется невырожденным, если его ядро состоит только из нулевого вектора.
Теорема 3.16 Пусть А – невырожденный линейный оператор в евклидовом пространстве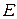 
. Тогда существуют ортогональный оператор 
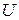и самосопряжённый оператор 
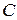с положительными собственными значениями (положительный оператор), такие, что 
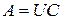– полярное разложение.
Замечание. На практике, надо умножить матрицу 
линейного оператора на матрицу 
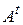. Из матрицы 
извлечь квадратный корень и получим симметрическую матрицу 
. С помощью элементарных преобразований из матрицы 
получим матрицу 
. Тогда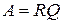 
.
Пример 14 Найти полярное разложение для матрицы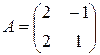 
линейного оператора, действующего в евклидовом пространстве.
Решение.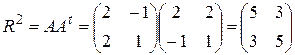 
.
Тогда,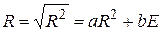 
. Найдем 
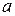и 
.
Найдем собственные значения матрицы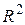 
: 
, 
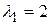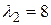. Они различны.
Функция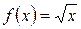 
. Составим и решим систему относительно 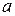и :
Тогда,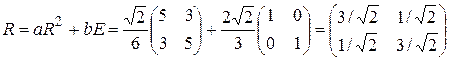 
.
Видим, что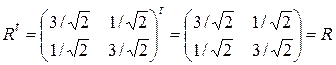 
.
В матрице 
получим на месте матрицы единичную матрицу:
.
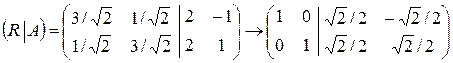Тогда,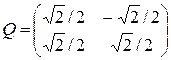 
. Мы видим, что
.
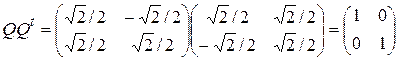Получили полярное разложение 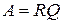, т.е.
.
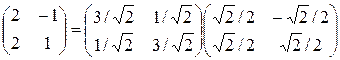Date: 2015-08-24; view: 8303; Нарушение авторских прав