Квадратичные формы

Пусть – симметричная билинейная форма, заданная на линейном пространстве .

Квадратичной формой называется числовая функция одного векторного аргумента , которая получается из билинейной формы при .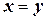

Пример 1 Дана симметрическая билинейная функция 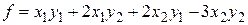. Найти квадратичную форму, ассоциированную с этой симметрической билинейной функцией.

Заменим в формуле симметрической билинейной функции букву на букву . Тогда квадратичная форма имеет вид: .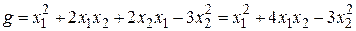

Симметричная билинейная форма называется полярной к квадратичной форме .

Полярная билинейная форма и квадратичная форма связаны следующим соотношением (поляризация):

,

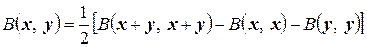которое вытекает из очевидного равенства

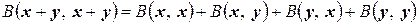
и свойства симметрии формы .

Пример 2 Найти поляризацию квадратичной формы .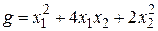

Пусть 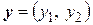. Тогда 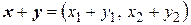. Поляризация квадратичной формы равна:

.

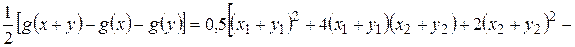
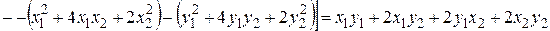Пусть в конечномерном линейном пространстве задана симметричная билинейная форма , полярная к квадратичной форме . Пусть, кроме того, в указан базис .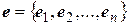

Согласно теореме 4.1 форму можно представить в виде (4.3)

,

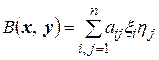где 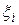и 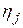– координаты в базисе 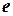векторов и соответственно. При этом в силу симметрии : .

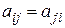Полагая в (4.3) 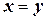(т.е. 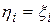) мы получим следующее представление для квадратичной формы в конечномерном пространстве с заданным базисом :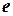

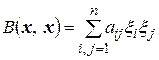. (4.11)

Матрица 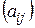называется матрицей квадратичной формы в заданном базисе .

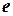Матрица 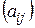является симметричной. Очевидно, каждой симметричной матрице 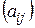отвечает с помощью соотношения (4.11) квадратичная форма , причем (4.11) будет представлением в пространстве с заданным базисом .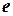

Отметим, что матрица квадратичной формы при переходе к новому базису преобразуется по формуле (4.7). Поэтому ранг этой матрицы не меняется при переходе к новому базису.

Обычно ранг матрицы квадратичной формы называется рангом квадратичной формы.

Если ранг матрицы квадратичной формы равен размерности пространства , то форма называется невырожденной, а в противном случае – вырожденной.

В дальнейшем мы будем использовать следующую терминологию.

Квадратичная форма называется:

1) положительно (отрицательно) определенной, если для любого ненулевого выполняется неравенство

()

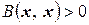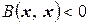(такие формы называются также знакоопределенными);

2) знакопеременной, если существуют такие и у, что

, ;

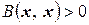3) квазизнакоопределенной, если для всех

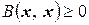или ,

но имеется отличный от нуля вектор , для которого .

В дальнейшем мы укажем признаки, по которым можно судить о принадлежности формы к одному из указанных типов.

Отметим следующее важное утверждение.

Если представляет собой билинейную форму, полярную положительно определенной квадратичной форме , то удовлетворяет всем аксиомам скалярного произведения векторов в евклидовом пространстве.

Обратимся к четырем аксиомам скалярного произведения.

Если число, называемое скалярным произведением векторов и у, обозначить символом , то эти аксиомы запишутся следующим образом:

1°. .

2°. .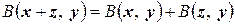

3°. .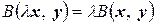

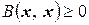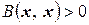4°. и при .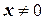

Так как билинейная форма полярная квадратичной форме симметрична, то аксиома 1° выполняется. Аксиомы 2° и 3° в сочетании с требованием симметрии выполнены в силу определения билинейной формы. Аксиома 4° выполняется, так как квадратичная форма положительно определена.

Замечание. Очевидно, аксиомы скалярного произведения можно рассматривать как совокупность требований, определяющих билинейную форму, полярную положительно определенной квадратичной форме. Поэтому скалярное произведение в линейных пространствах может быть задано с помощью такого вида билинейной формы.

Date: 2015-08-24; view: 4477; Нарушение авторских прав