Закон инерции квадратичных форм. Классификация квадратичных форм

Закон инерции квадратичных форм. Мы уже отмечали выше, что ранг квадратичной формы равен числу отличных от нуля канонических коэффициентов. Таким образом, число отличных от нуля канонических коэффициентов не зависит от выбора невырожденного преобразования, с помощью которого форма приводится к каноническому виду. На самом деле при любом способе приведения формы к каноническому виду не меняется число положительных и отрицательных канонических коэффициентов. Это свойство называется законом инерции квадратичных форм.

Пусть форма в базисе 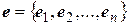определяется матрицей :

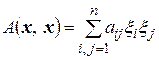, (4.20)

где – координаты вектора в базисе е. Допустим, что эта форма с помощью невырожденного преобразования координат приведена к каноническому виду

, (4.21)

причем 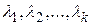– отличные от нуля канонические коэффициенты, занумерованные так, что первые 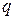из этих коэффициентов положительные, а следующие коэффициенты – отрицательные:

, , …, , , …, .

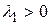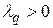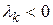Рассмотрим следующее невырожденное преобразование координат :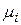

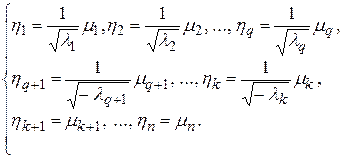(4.22)

В результате этого преобразования форма примет вид

, (4.23)

называемый нормальным видом квадратичной формы.

Теорема 4.5 (закон инерции квадратичных форм). Число слагаемых с положительными (отрицательными) коэффициентами в нормальном виде квадратичной формы не зависит от способа приведения формы к этому виду.

Следствие. Две квадратичные формы эквивалентны тогда и только тогда, когда ранги форм равны, положительные и отрицательные индексы инерции совпадают.

Классификация квадратичных форм. В этом пункте с помощью понятий индекса инерции, положительного и отрицательного индексов инерции квадратичной формы мы укажем, каким образом можно выяснить принадлежность квадратичной формы к тому или иному из перечисленных выше типов (положительно определенной, отрицательно определенной, знакопеременной и квазизнакоопределенной). При этом индексом инерции квадратичной формы мы будем называть число отличных от нуля канонических коэффициентов этой формы (т.е. ее ранг), положительным индексом инерции – число положительных канонических коэффициентов, отрицательным индексом инерции – число отрицательных канонических коэффициентов. Ясно, что сумма положительного и отрицательного индексов инерции равна индексу инерции. Отрицательный и положительный индексы инерции связаны соотношением 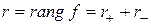, а пара 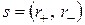или 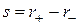называется сигнатурой квадратичной формы.

Итак, пусть индекс инерции, положительный и отрицательный индексы инерции квадратичной формы соответственно равны 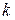, 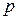и 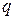(). В предыдущем пункте было доказано, что в любом каноническом базисе 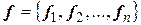эта форма может быть приведена к следующему нормальному виду:

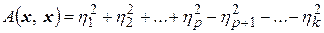, (4.24)

где – координаты вектора в базисе .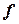

Пример 6 Найти нормальный вид и сигнатуру квадратичной формы

.

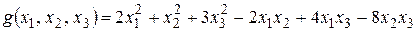Канонический вид этой формы имеет вид: 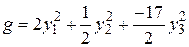. Положим 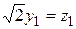, , 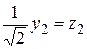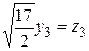. Тогда 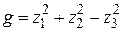. Это нормальный вид квадратичной формы. Положительный индекс инерции: , отрицательный индекс инерции 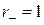. Следовательно, сигнатура квадратичной формы .

Теорема 4.6 (необходимое и достаточное условие знакоопределенности квадратичной формы) Для того чтобы квадратичная форма , заданная в n-мерном линейном пространстве L, была знакоопределенной, необходимо и достаточно, чтобы либо положительный индекс инерции 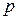, либо отрицательный индекс инерции 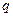был равен размерности 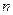пространства L. При этом, если 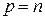, то форма положительно определенная, если же , то форма отрицательно определенная.

Замечание. Для выяснения вопроса о знакоопределенности квадратичной формы с помощью указанного признака мы должны привести эту форму к каноническому виду.

Теорема 4.7 (необходимое и достаточное условие знакопеременности квадратичной формы) Для того чтобы квадратичная форма была знакопеременной, необходимо и достаточно, чтобы как положительный, так и отрицательный индексы инерции этой формы были отличны от нуля.

Теорема 4.8 (необходимое и достаточное условие квазизнакоопределенности квадратичной формы) Для того чтобы форма была квазизнакоопределенной, необходимо и достаточно, чтобы выполнялись соотношения: либо , , 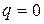либо , .

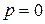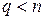Критерий Сильвестра знакоопределенности квадратичной формы. Пусть форма в базисе 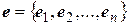определяется матрицей : 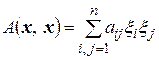и пусть 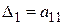, , 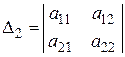…, 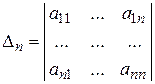– угловые (главные) миноры и определитель матрицы 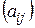. Справедливо следующее утверждение:

Теорема 4.9 (критерий Сильвестра) Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы были выполнены неравенства , , …, .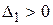

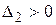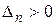Для того чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы знаки угловых миноров чередовались, причем .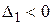

Следствие 1 Для того чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы все угловые миноры четного порядка были положительны и все угловые миноры нечетного порядка были отрицательны или, иначе, были выполнены неравенства , , …, , .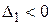

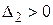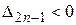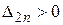Следствие 2 Для того чтобы квадратичная форма была неотрицательной, необходимо и достаточно, чтобы все главные (не только угловые) миноры ее матрицы были неотрицательны.

Следствие 3 Для того чтобы квадратичная форма была неположительной, необходимо и достаточно, чтобы все главные миноры четного порядка были неотрицательны и все главные миноры нечетного порядка были неположительны.

Следствие 4 Для того чтобы квадратичная форма была неопределенной (знакопеременной), необходимо и достаточно, чтобы у ее матрицы существовали отрицательный главный минор четного порядка и два главных минора нечетных порядков разных знаков.

Пример 7 Исследовать квадратичные формы на знакоопределенность:

1) ,

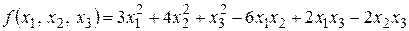2) ,

3) ,

4) ,

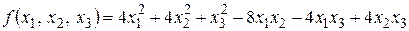5) .

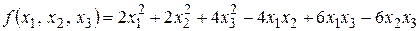Решение.

1) Для матрицы квадратичной формы 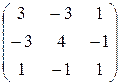найдем все угловые миноры

, , .

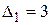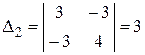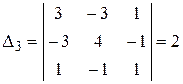Все угловые миноры положительны, значит квадратичная форма положительно определенная.

2) Матрица квадратичной формы . Ее угловые миноры

, , .

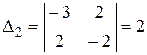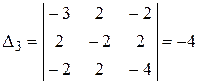Оба угловых минора нечетного порядка отрицательны и угловой минор четного порядка положителен. Значит, квадратичная форма отрицательно определена.

3) Матрица квадратичной формы 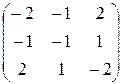. Ее угловые миноры

, , .

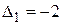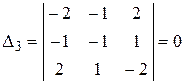В этом случае только по значениям угловых миноров дать ответ нельзя. Найдем все главные миноры. Кроме углового есть еще два главных миноры первого порядка, равны –1 и –2. Не угловые главные миноры второго порядка , 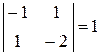. Таким образом, все главные миноры нечетного порядка неположительны и все главные миноры четного порядка неотрицательны. Значит, квадратичная форма неположительна.

4) Матрица квадратичной формы 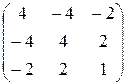. Ее угловые миноры

, , .

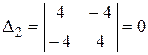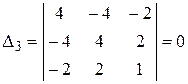В этом случае только по значениям угловых миноров дать ответ нельзя. Найдем все главные миноры. Остальные главные миноры первого порядка равны 4 и 1. Не угловые главные миноры второго порядк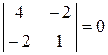а , . Таким образом, все главные миноры неотрицательны. Значит, квадратичная форма неотрицательна.

5) Матрица квадратичной формы 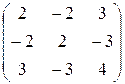. Ее угловые миноры

, , .

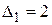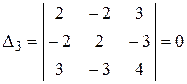В этом случае опять только по значениям угловых миноров дать ответ нельзя. Найдем все главные миноры. Не угловые главные миноры первого порядка равны 2 и 4. Не угловые главные миноры второго порядка 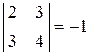, 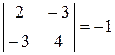. Имеется отрицательный главный минор четного порядка. Поэтому квадратичная форма неопределенная.

Date: 2015-08-24; view: 1835; Нарушение авторских прав