
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Линейные операторы в евклидовом пространстве
|
|
3.1 Сопряженный оператор
Пусть 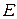 – евклидово пространство.
– евклидово пространство.
Линейный оператор 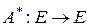 называется сопряженным к линейному оператору
называется сопряженным к линейному оператору  , если для любых
, если для любых  и
и  из
из 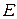 выполняется соотношение
выполняется соотношение
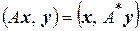 . (3.1)
. (3.1)
Легко убедиться в том, что оператор 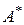 , сопряженный к линейному оператору А, сам является линейным оператором. Это следует из очевидного соотношения
, сопряженный к линейному оператору А, сам является линейным оператором. Это следует из очевидного соотношения
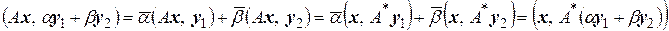 ,
,
справедливого для любых элементов  ,
, 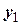 ,
,  и любых комплексных чисел α и β.
и любых комплексных чисел α и β.
Лемма 3.1 Если квадратные матрицы М и N порядка п таковы, что для любых вектор-столбцов  выполняется соотношение
выполняется соотношение 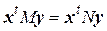 , то
, то 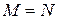 .
.
Теорема 3.1 Любому линейному оператору  соответствует единственный сопряженный оператор
соответствует единственный сопряженный оператор 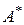 , причем его матрицей в любом ортонормированном базисе
, причем его матрицей в любом ортонормированном базисе 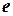 является матрица
является матрица 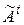 , транспонированная матрице
, транспонированная матрице 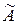 линейного оператора А в том же базисе
линейного оператора А в том же базисе 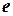 .
.
Пример 1 Вектор  порождает линейный оператор
порождает линейный оператор 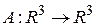 согласно формуле
согласно формуле
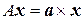 .
.
Оператор, сопряженный к оператору А, можно определить, опираясь на свойства скалярного, векторного и смешанного произведений:
 .
.
Из приведенных соотношений видно, что 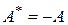 .
.
Пример 2 Линейное пространство  бесконечно дифференцируемых на отрезке
бесконечно дифференцируемых на отрезке 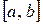 функций, у которых в точках
функций, у которых в точках 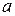 и
и  производные любого порядка равны нулю со скалярным произведением
производные любого порядка равны нулю со скалярным произведением 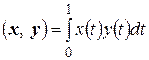 (см. 2.1). Отображение
(см. 2.1). Отображение  , которое каждой функции
, которое каждой функции 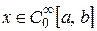 ставит в соответствие ее производную, является линейным оператором. Оператором, сопряженным к А, будет
ставит в соответствие ее производную, является линейным оператором. Оператором, сопряженным к А, будет  , поскольку, согласно
, поскольку, согласно
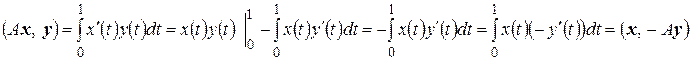 .
.
Отметим следующие свойства сопряженных операторов:
1. 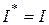 . 4.
. 4. 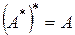 .
.
2. 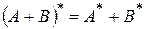 . 5.
. 5. 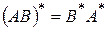 .
.
3. 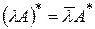 .
.
Замечание. Понятие сопряженного оператора для вещественного пространства вводится совершенно аналогично. Выводы этого пункта и свойства сопряженных операторов справедливы и для этого случая (при этом свойство 3 формулируется так: ( ).
).
Пример 3 В базисе 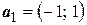 ,
, 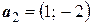 евклидова пространства
евклидова пространства 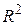 известна матрица
известна матрица 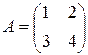 линейного оператора. Определить матрицу сопряженного оператора в этом базисе.
линейного оператора. Определить матрицу сопряженного оператора в этом базисе.
Решение. Определим элементы матрицы Грамма базисных векторов  ,
,  :
:
 ,
, 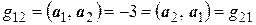 ,
, 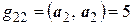 .
.
Тогда,  . Отсюда,
. Отсюда, 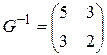 . Поэтому матрица сопряженного оператора в базисе
. Поэтому матрица сопряженного оператора в базисе  ,
,  равна
равна 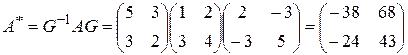 .
.
Пример 4 Пусть 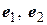 – ортонормированный базис в унитарном пространстве
– ортонормированный базис в унитарном пространстве 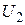 ,
, 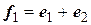 ,
,  . Линейный оператор
. Линейный оператор  , действующий в этом пространстве, имеет в базисе
, действующий в этом пространстве, имеет в базисе 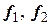 матрицу
матрицу 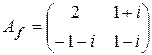 . Найти матрицу сопряженного оператора
. Найти матрицу сопряженного оператора  в базисе
в базисе 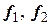 .
.
Решение. Матрица 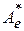 оператора
оператора  в ортонормированном базисе
в ортонормированном базисе 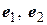 связана с матрицей
связана с матрицей 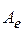 оператора
оператора  равенством
равенством  . При переходе к базису
. При переходе к базису 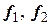 матрица оператора
матрица оператора  преобразуется по формуле
преобразуется по формуле  , где
, где 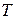 – матрица перехода от базиса
– матрица перехода от базиса 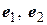 к базису
к базису 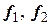 , т.е.
, т.е. 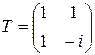 . Аналогично, матрица
. Аналогично, матрица  связана с матрицей
связана с матрицей 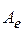 соотношением
соотношением 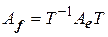 . Отсюда следует, что
. Отсюда следует, что 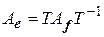 и, следовательно,
и, следовательно, 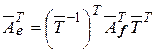 . Таким образом, получаем
. Таким образом, получаем
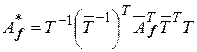 .
.
Так как  , то
, то
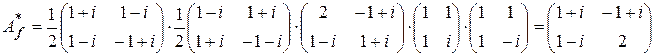 .
.
Date: 2015-08-24; view: 1541; Нарушение авторских прав