Билинейные и квадратичные формы в евклидовом пространстве

В предыдущих параграфах мы изучали билинейные и квадратичные формы в произвольном (не обязательно евклидовом) вещественном линейном пространстве L. В этом параграфе мы получим ряд сведений о билинейных и квадратичных формах, заданных в вещественном евклидовом пространстве.

Рассмотрим билинейную форму , заданную в евклидовом пространстве V. Каждой такой форме однозначно соответствует линейный оператор такой, что справедливо равенство

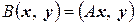. (4.25)

Кроме того, можно доказать, что билинейная форма является симметричной тогда и только тогда, когда оператор А, фигурирующий в (4.25), является самосопряженным.

Напомним также, что для любого самосопряженного оператора А было доказано существование ортонормированного базиса из собственных векторов Это означает, что существуют ортонормированная система 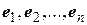и вещественные числа 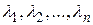такие, что

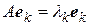. (4.26)

Отметим, что в базисе 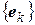матрица оператора А имеет диагональный вид.

Приведение квадратичной формы к сумме квадратов в ортогональном базисе. Пусть – симметричная билинейная форма, заданная в вещественном евклидовом пространстве V, а – определяемая ею квадратичная форма.

Докажем следующую теорему о приведении квадратичной формы к сумме квадратов.

Теорема 4.10 Пусть – симметричная билинейная форма, заданная в евклидовом пространстве V. Тогда в пространстве V существует такой ортонормированный базис 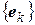и можно указать такие вещественные числа 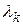, что для любого 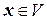квадратичная форма может быть представлена в виде следующей суммы квадратов координат 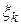вектора в базисе :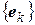

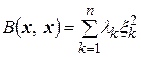. (4.39)

Сказанное выше позволяет сформулировать основные этапы приведения действительной квадратичной формы к каноническому виду ортогональным преобразованием переменных:

1. Записать матрицу А рассматриваемой квадратичной формы.

2. Определить из уравнения 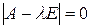собственные значения этой матрицы (они все действительны, так как матрица А симметрична).

3. Для каждого собственного значения 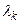определить соответствующие ему линейно независимые собственные векторы (n -мерные матрицы-столбцы).

4. К полученным собственным векторам, отвечающим собственному значению 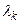, применить процесс ортогонализации.

5. После того, как будут найдены все n собственных векторов матрицы А, образующие ортонормированный базис 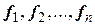в n -мерном действительном евклидовом пространстве матриц-столбцов, нужно координаты векторов 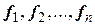поместить в соответствующие столбцы искомой матрицы Q.

6. Написать канонический вид квадратичной формы

,

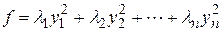где 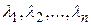собственные значения матрицы А.

7. Записать вид линейного преобразования переменных

,

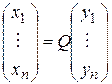которое приводит заданную квадратичную форму 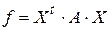к каноническому виду.

Пример 8 Привести ортогональным преобразованием переменных квадратичную форму 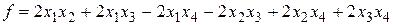к каноническому виду.

Решение. Запишем матрицу заданной квадратичной формы

.

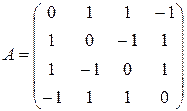Составим характеристическое уравнение :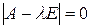

.

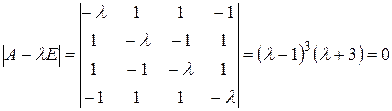Собственными значениями матрицы А являются числа 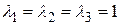, 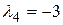. Отсюда вытекает, что квадратичная форма f имеет такой канонический вид

.

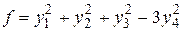При 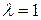система уравнений для определения координат собственных векторов имеет вид

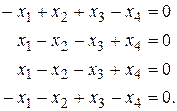
Так как 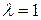является корнем характеристического уравнения третьей кратности, то ему соответствуют три линейно независимых собственных вектора. Это означает, что фундаментальная система решений рассматриваемой однородной системы уравнений должна состоять из трех линейно независимых решений рассматриваемой системы уравнений. Следовательно, ранг матрицы системы однородных уравнений 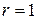и, поэтому, система уравнений эквивалентна одному из своих уравнений, например, второму уравнению, ФСР которой имеет вид:

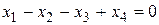
	–1

Векторы , , 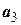являются линейно независимыми собственными векторами матрицы А, которые отвечают собственному значению 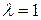. Любой собственный вектор матрицы А, отвечающий собственному значению 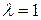, является линейной комбинацией векторов , , , 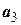так как координаты этого вектора удовлетворяют системе уравнений.

Применим процесс ортогонализации к системе векторов , , 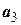получим ортонормированную совокупность линейно независимых собственных векторов 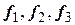матрицы А, отвечающих собственному значению 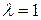. Имеем

;

, , , ;

, , , .

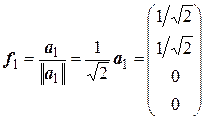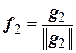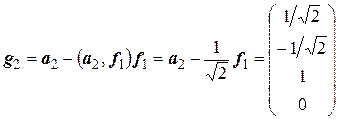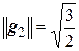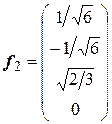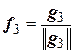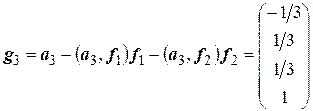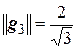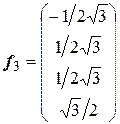При 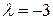согласно получаем следующую систему уравнений для определения координат собственного вектора 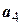матрицы А

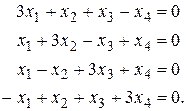
Матрица этой системы имеет ранг, равный трем, поэтому фундаментальная система решений состоит из одного ненулевого решения 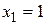, , 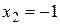, 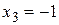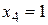. Собственный вектор 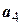оказывается таким: .

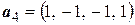Нормированный собственный вектор: .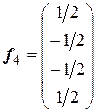

Составим матрицу Q ортогонального преобразования переменных, которое приводит квадратичную форму к каноническому виду. Для этого поместим в столбцы матрицы Q координаты собственных векторов 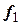, , , , 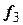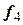получим

.

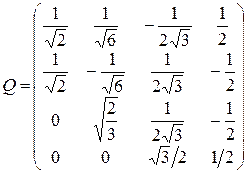Таким образом, квадратичная форма 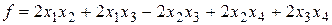при помощи ортогонального преобразования переменных

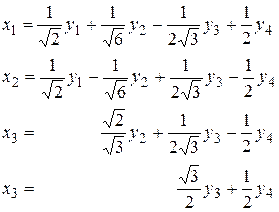
приводится к каноническому виду

.

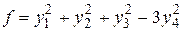Заметим, что форма f не является положительно определенной.

Две квадратичные формы будут эквивалентными на данным полем, если у них будут равны ранги и сигнатуры.

Пример 9 Для квадратичных форм 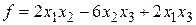и 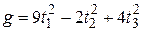определить, эквивалентны ли они над полем ? Если да, то найти преобразование, переводящее форму 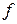в форму .

Решение. Выше был получен канонический вид для формы 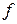: 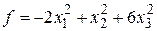. Найдем индексы инерции и сигнатуру: , 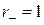и сигнатура . Для формы : , 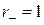и сигнатура . Итак, формы эквивалентны.

Найдем теперь преобразование, переводящее форму 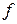в форму . Форма 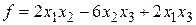приводится к нормальному виду 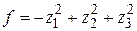заменой

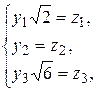
где 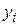, 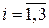определяются соотношениями:

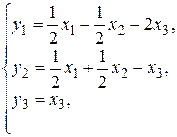
т.е.

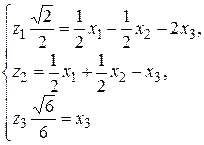или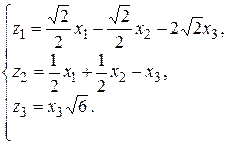

Форму 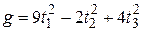заменой 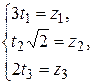приводим к нормальному виду .

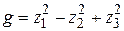Итак, искомое преобразование, переводящее форму 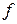в форму :

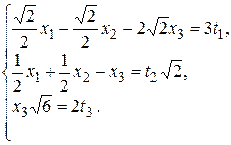
Или, выразив 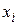через 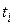, , 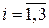будем иметь:

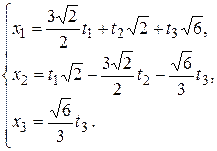
Date: 2015-08-24; view: 2080; Нарушение авторских прав