Самосопряженный (симметричный) оператор

Линейный оператор А, действующий в унитарном (евклидовом) пространстве, называют самосопряженным (симметричным (эрмитовым)), если 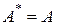или если для любых векторов и верно равенство

.

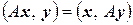Линейный оператор А, действующий в евклидовом пространстве, называют кососимметричным (косоэрмитовым), ес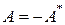ли или .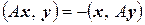

Действительно, если указанное соотношение выполняется, то, согласно первому определению, линейный оператор А является сопряженным оператором к самому себе, т.е. .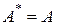

Пример 5 Самосопряженными являются простейшие линейные операторы: нулевой 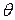и тождественный 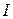, так как для любых векторов и

,

.

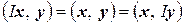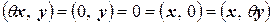Самосопряженный оператор в вещественном пространстве определяется аналогично.

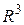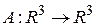Пример 6 Рассмотрим линейное пространство с обычным скалярным произведением свободных векторов . Отображение ортогонального проектирования векторов из 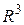на направление вектора 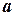единичной длины, которое определяется формулой 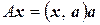, является линейным оператором, так как

.

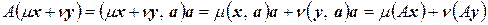Убедимся, что этот оператор является самосопряженным:

.

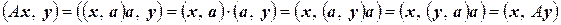Теорема 3.2 Матрица самосопряженного оператора в любом ортонормированном базисе является симметрической 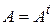(эрмитовой). Наоборот, если матрица линейного оператора в некотором ортонормированном базисе является симметрической (эрмитовой), то этот оператор – самосопряженный.

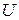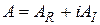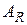Теорема 3.3 Пусть А – линейный оператор, действующий в комплексном евклидовом пространстве . Тогда справедливо представление , где и 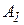– самосопряженные операторы, называемые соответственно действительной и мнимой частью оператора А.

Мы будем говорить, что операторы А и В коммутируют, если .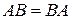

Теорема 3.4 Для того чтобы произведение АВ самосопряженных операторов А и В было самосопряженным оператором, необходимо и достаточно, чтобы они коммутировали.

В дальнейших теоремах устанавливается ряд важных свойств самосопряженных операторов.

Теорема 3.5 Если оператор А самосопряженный, то для любого 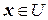скалярное произведение 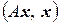– вещественное число.

Теорема 3.6 Собственные значения самосопряженного оператора вещественны.

Следствие 1 Если матрица является симметрической, то все корни ее характеристического уравнения действительные.

Следствие 2 Самосопряженный оператор, действующий в 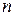-мерном евклидовом пространстве, имеет 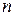собственных значений, если каждое из них считать столько раз, какова его кратность.

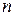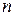Следствие 3 Симметрическая матрица порядка имеет собственных значений, если каждое из них считать столько раз, какова его кратность.

В следующей теореме выясняется свойство ортогональности собственных векторов самосопряженного оператора.

Теорема 3.7 Если А – самосопряженный оператор, то собственные векторы, отвечающие различным собственным значениям этого оператора, ортогональны.

Теорема 3. 8 (теорема Гамильтона-Кэли) Если – самосопряженный оператор и 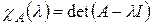– характеристический многочлен этого оператора, то .

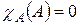Самосопряженный оператор А называется положительным, если для любого 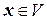справедливо соотношение

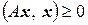. (3.14)

Если оператор А – положительный и из условия 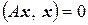следует, что 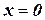, то А называется положительно определенным оператором.

Положительные и положительно определенные операторы соответственно обозначаются символами и .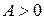

Теорема 3.9 Каждое собственное значение положительного (положительно определенного) оператора неотрицательно (положительно).

Теорема 3.10 У каждого самосопряженного линейного оператора А, действующего в n-мерном евклидовом пространстве V существует 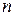линейно независимых попарно ортогональных и единичных собственных векторов.

Замечание 1 Договоримся в дальнейшем нумеровать собственные значения самосопряженного оператора в порядке убывания с учетом повторяющихся, т.е. кратных собственных значений. При этом 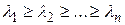и отвечающие им собственные векторы 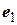, , 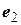…, можно считать взаимно ортогональными и удовлетворяющими условию .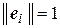

Пример 7 В линейной оболочке 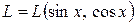скалярное произведение элементов 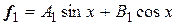и 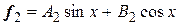введено по формуле

.

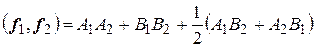а) доказать, что элементы 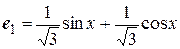и 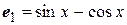образуют ортонормированный базис пространства .

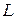б) найти матрицу оператора дифференцирования 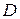в базисе , .

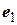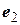в) найти матрицу сопряженного оператора 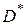в базисе , .

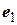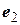г) справедливо ли равенство ?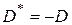

д) является ли оператор 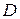симметричным в пространстве ?

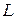Решение.

а) Так как ,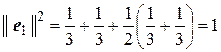

, ,

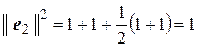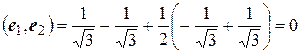то 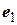, 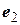– ортонормированный базис пространства .

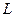б) Найдем матрицу 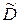оператора 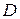в базисе 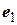, 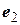. Действуя оператором 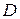на базисные элементы 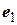и 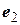, получаем:

,

.

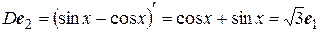Отсюда следует, что 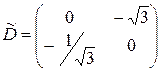– матрица оператора 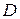в базисе , .

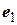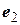в) Матрица 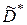сопряженного оператора 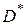в базисе 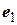, 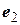является транспонированной по отношению к матрице 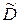, т.е. .

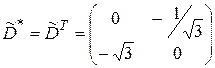г) сравнивая матрицы 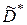и 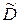, приходим к выводу, что 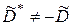. Следовательно, не равны и соответствующие операторы: .

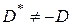д) так как матрица 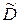оператора 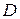в ортонормированном базисе 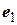, 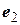не является симметричной, то и оператор не является симметричным.

Пример 8 Является ли эрмитовым оператор , если в некотором ортонормированном базисе он имеет матрицу:

а) 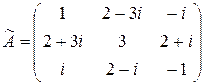; б) ?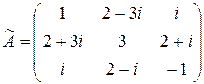

Решение.

а) так как 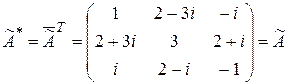, то 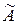– эрмитова матрица, и, следовательно, – эрмитов оператор.

б) так как 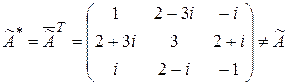, то 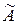не является эрмитовой матрицей, и, следовательно, не является эрмитовым оператором.

Пример 9 Пусть – линейный оператор, действующий в унитарном пространстве. Доказать, что оператор 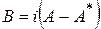является эрмитовым оператором.

Решение. Оператор является эрмитовым, если он равен сопряженному оператору, т.е. 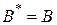. Используя свойства сопряженного оператора, получим

.

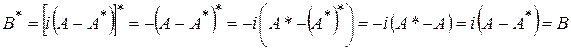Date: 2015-08-24; view: 3373; Нарушение авторских прав