
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Для любого элемента и любого вещественного числа
|
|
3°. Для любых двух элементов  и
и  справедливо следующее неравенство:
справедливо следующее неравенство:
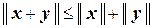 , (2.3)
, (2.3)
называемое неравенством треугольника (или неравенством Минковского).
Теорема 2.2 Всякое евклидово пространство является нормированным, если в нем норму любого элемента  определить равенством
определить равенством
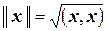 . (2.4)
. (2.4)
Следствие. Во всяком евклидовом пространстве с нормой элементов, определяемой соотношением (2.4), для любых двух элементов  и
и  справедливо неравенство треугольника (2.3).
справедливо неравенство треугольника (2.3).
Заметим далее, что в любом вещественном евклидовом пространстве можно ввести понятие угла между двумя произвольными элементами  и
и  этого пространства. В полной аналогии с векторной алгеброй, мы назовем углом
этого пространства. В полной аналогии с векторной алгеброй, мы назовем углом 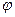 между элементами
между элементами  и
и  тот (изменяющийся в пределах от 0 до π) угол, косинус которого определяется соотношением
тот (изменяющийся в пределах от 0 до π) угол, косинус которого определяется соотношением
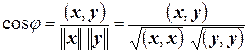 .
.
Данное нами определение угла корректно, ибо в силу неравенства Коши-Буняковского (2.1) дробь, стоящая в правой части последнего равенства, по модулю не превосходит единицы.
Пример 5 Пусть 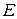 – евклидово пространство, элементами которого являются действительные функции, непрерывные на отрезке
– евклидово пространство, элементами которого являются действительные функции, непрерывные на отрезке 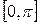 . Скалярное произведение двух произвольных элементов
. Скалярное произведение двух произвольных элементов 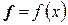 и
и 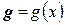 пространства
пространства 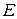 определим известным способом
определим известным способом  . Требуется найти угол между элементами
. Требуется найти угол между элементами 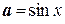 и
и  .
.
Решение. Согласно определению скалярного произведения
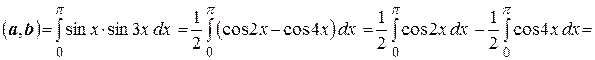
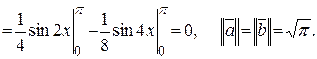
На основании формулы угла  , следовательно, угол между элементами
, следовательно, угол между элементами  и
и  пространства
пространства 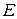 равен
равен  .
.
Далее договоримся называть два произвольных элемента  и
и  евклидова пространства
евклидова пространства 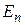 ортогональными, если скалярное произведение этих элементов
ортогональными, если скалярное произведение этих элементов 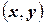 равно нулю (в этом случае косинус угла
равно нулю (в этом случае косинус угла  между элементами
между элементами  и
и  будет равен нулю).
будет равен нулю).
Сумму  двух ортогональных элементов
двух ортогональных элементов  и
и  будем называть гипотенузой прямоугольного треугольника с катетами
будем называть гипотенузой прямоугольного треугольника с катетами  и
и  .
.
Теорема 2.2 (Пифагора) Квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин катетов.
В заключение запишем норму, неравенство Коши-Буняковского и неравенство треугольника в каждом из конкретных евклидовых пространств, рассмотренных в предыдущем пункте.
В евклидовом пространстве всех свободных векторов с обычным определением скалярного произведения норма вектора а совпадает с его длиной 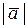 , неравенство Коши-Буняковского приводится к виду
, неравенство Коши-Буняковского приводится к виду  , а неравенство треугольника – к виду
, а неравенство треугольника – к виду 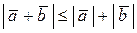 .
.
В евклидовом пространстве 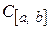 всех непрерывных на сегменте
всех непрерывных на сегменте 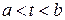 функций
функций 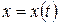 норма элемента
норма элемента 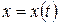 равна
равна  , а неравенства Коши-Буняковского и треугольника имеют вид
, а неравенства Коши-Буняковского и треугольника имеют вид
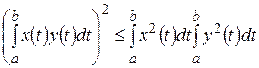 ,
, 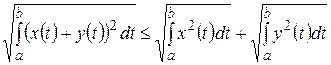 .
.
В евклидовом пространстве 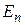 упорядоченных совокупностей
упорядоченных совокупностей  вещественных чисел норма любого элемента
вещественных чисел норма любого элемента 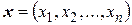 равна
равна
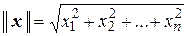 ,
,
а неравенства Коши-Буняковского и треугольника имеют вид
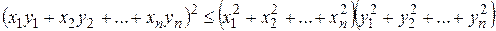 ,
,
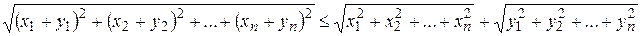 .
.
Два евклидовых пространства Ε и Е' называются изоморфными, если между элементами этих пространств можно установить взаимно однозначное соответствие так, что если элементам  и
и  пространства Ε отвечают соответственно элементы
пространства Ε отвечают соответственно элементы  и
и 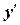 пространства Е', то элементу
пространства Е', то элементу 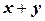 отвечает элемент
отвечает элемент 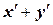 , элементу
, элементу  (при любом вещественном λ) отвечает элемент
(при любом вещественном λ) отвечает элемент  и скалярное произведение
и скалярное произведение 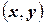 равно скалярному произведению
равно скалярному произведению 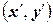 .
.
Таким образом, евклидовы пространства Ε и Е' изоморфны, если они изоморфны как линейные пространства и если этот изоморфизм сохраняет величину скалярного произведения соответствующих пар элементов.
Теорема 2.3 Все евклидовы пространства одной и той же размерности  изоморфны между собой.
изоморфны между собой.
Данная теорема позволяет утверждать, что если в каком-нибудь конкретном  -мерном евклидовом пространстве Е' доказана теорема, сформулированная в терминах операций сложения, умножения на числа и скалярного перемножения элементов, то эта теорема справедлива и в совершенно произвольном
-мерном евклидовом пространстве Е' доказана теорема, сформулированная в терминах операций сложения, умножения на числа и скалярного перемножения элементов, то эта теорема справедлива и в совершенно произвольном  -мерном евклидовом пространстве Е.
-мерном евклидовом пространстве Е.
2.2 Ортонормированный базис конечномерного евклидова пространства
Будем говорить, что  элементов
элементов 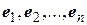
 -мерного евклидова пространства
-мерного евклидова пространства 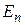 образуют ортонормированный базис этого пространства, если эти элементы попарно ортогональны и норма каждого из этих элементов равна единице, т.е. если
образуют ортонормированный базис этого пространства, если эти элементы попарно ортогональны и норма каждого из этих элементов равна единице, т.е. если
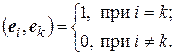 (2.5)
(2.5)
Примером ортонормированного базиса может служить декартов прямоугольный базис евклидова пространства всех свободных векторов или совокупность  элементов
элементов  ,
,  , …,
, …,  евклидова пространства всех упорядоченных совокупностей
евклидова пространства всех упорядоченных совокупностей  вещественных чисел.
вещественных чисел.
Докажем теперь следующую основную теорему.
Теорема 2.4 Во всяком  -мерном евклидовом пространстве
-мерном евклидовом пространстве 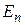 существует ортонормированный базис.
существует ортонормированный базис.
Доказательство. Согласно определению размерности в пространстве 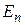 найдется
найдется  линейно независимых элементов
линейно независимых элементов 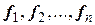 .
.
Докажем, что можно построить  элементов
элементов 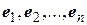 , линейно выражающихся через
, линейно выражающихся через 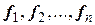 , и, образующих ортонормированный базис (т.е. удовлетворяющих соотношениям (2.5)).
, и, образующих ортонормированный базис (т.е. удовлетворяющих соотношениям (2.5)).
Проведем доказательство возможности построения таких элементов 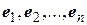 методом математической индукции.
методом математической индукции.
Если имеется только один элемент 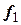 , то для построения элемента
, то для построения элемента 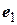 с нормой, равной единице, достаточно нормировать элемент
с нормой, равной единице, достаточно нормировать элемент 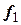 , т.е. положим
, т.е. положим
 .
.
Из элементов 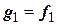 и
и  образуем
образуем 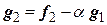 . Число
. Число  возьмем таким, чтобы
возьмем таким, чтобы  . Имеем
. Имеем
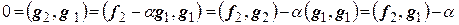 .
.
Следовательно, 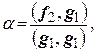 а
а  . Положим
. Положим
 .
.
Единичный вектор 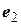 ортогонален вектору
ортогонален вектору 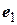 . Построим теперь вспомогательный вектор
. Построим теперь вспомогательный вектор  . Подберем числа
. Подберем числа 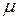 и
и 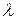 так, чтобы
так, чтобы 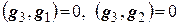 . Для определения этих чисел имеем уравнения
. Для определения этих чисел имеем уравнения
 .
.
Следовательно, 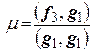 ,
,  , а
, а 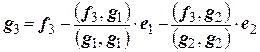 .
.
Единичный вектор
 .
.
очевидно, ортогонален единичным векторам 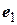 и
и 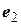 .
.
Продолжая процесс создания попарно ортогональных единичных векторов 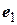 ,
, 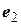 ,
, 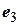 , …, построим за конечное число шагов ортонормированный базис
, …, построим за конечное число шагов ортонормированный базис  – мерного евклидового пространства.
– мерного евклидового пространства.
Заметим, что различных ортонормированных базисов евклидового пространства бесконечно много, так как бесконечно много базисов 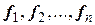 , из которых процессом ортогонализации можно создавать ортонормированные.
, из которых процессом ортогонализации можно создавать ортонормированные.
Доказанная теорема приводит к следующему осуществляемому шаг за шагом алгоритму построения по данной системе  линейно независимых элементов
линейно независимых элементов 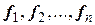 системы
системы  попарно ортогональных элементов
попарно ортогональных элементов 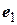 ,
, 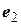 , …,
, …,  , норма каждого из которых равна единице:
, норма каждого из которых равна единице:
Указанный алгоритм обычно называют процессом ортогонализации линейно независимых элементов 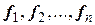 ·(процесс ортогонализации Грамма-Шмидта).
·(процесс ортогонализации Грамма-Шмидта).
Замечание. Конечно, в каждом  -мерном евклидовом пространстве существует много ортонормированных базисов. Действительно, если например, строить ортонормированный базис процессом ортогонализации одних и тех же линейно независимых элементов
-мерном евклидовом пространстве существует много ортонормированных базисов. Действительно, если например, строить ортонормированный базис процессом ортогонализации одних и тех же линейно независимых элементов 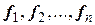 , то, начиная процесс ортогонализации с различных элементов
, то, начиная процесс ортогонализации с различных элементов  , мы придем к различным ортонормированным базисам.
, мы придем к различным ортонормированным базисам.
Пример 6 Применить процесс ортогонализации Грамма-Шмидта к системе векторов 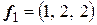 ,
, 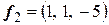 ,
, 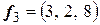 .
.
Решение. Сначала построим ортогональный базис  :
:
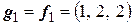 ,
,

или 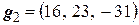 ,
,


или  .
.
Построен ортогональный базис  . Получим из него ортонормированный базис
. Получим из него ортонормированный базис 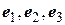 :
:
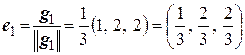 ,
,
 ,
,
 .
.
Свойства ортонормированного базиса. Пусть 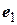 ,
, 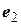 , …,
, …,  – произвольный ортонормированный базис
– произвольный ортонормированный базис  -мерного евклидова пространства, а
-мерного евклидова пространства, а  и
и  – два произвольных элемента этого пространства. Найдем выражение скалярного произведения
– два произвольных элемента этого пространства. Найдем выражение скалярного произведения 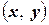 этих элементов через их координаты относительно базиса
этих элементов через их координаты относительно базиса 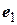 ,
, 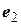 , …,
, …,  .
.
Обозначим координаты элементов  и
и  относительно базиса
относительно базиса 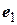 ,
, 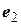 , …,
, …,  соответственно через
соответственно через 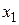 ,
, 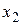 , …,
, …, 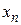 и
и  ,
, 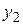 , …,
, …, 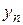 , т.е. предположим, что
, т.е. предположим, что 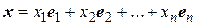 ,
,  . Тогда
. Тогда
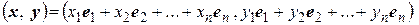
или
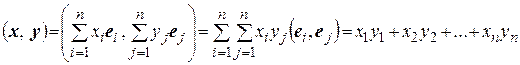 . (2.7)
. (2.7)
Таким образом, в ортонормированном базисе скалярное произведение двух любых элементов равно сумме произведений соответствующих координат этих элементов.
Рассмотрим теперь в  -мерном евклидовом пространстве совершенно произвольный (вообще говоря, не ортонормированный) базис
-мерном евклидовом пространстве совершенно произвольный (вообще говоря, не ортонормированный) базис 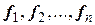 и найдем выражение скалярного произведения двух произвольных элементов
и найдем выражение скалярного произведения двух произвольных элементов  и
и  через координаты этих элементов относительно указанного базиса.
через координаты этих элементов относительно указанного базиса.
Обозначим координаты элементов  и
и  относительно базиса
относительно базиса 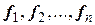 соответственно через
соответственно через 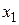 ,
, 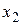 , …,
, …, 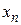 и
и  ,
, 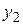 , …,
, …, 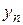 , т.е. предположим, что
, т.е. предположим, что
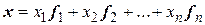 ,
, 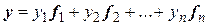 .
.
Пользуясь аксиомами скалярного произведения, получим
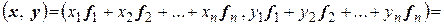
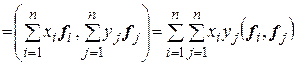 .
.
Таким образом, в произвольном базисе 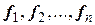 скалярное произведение двух любых элементов
скалярное произведение двух любых элементов 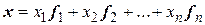 ,
, 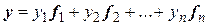 определяется равенством
определяется равенством
 , (2.8)
, (2.8)
где матрица 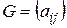 – матрица Грамма, (
– матрица Грамма, (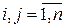 ) имеет элементы
) имеет элементы  ;
;  ;
; 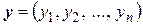 – матрицы-строки координат элементов
– матрицы-строки координат элементов  и
и  соответственно.
соответственно.
Матрице Грамма поставим в соответствие ее определитель: 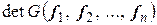 .
.
Свойства определителя Грамма:
1. 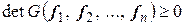 .
.
2.  – линейно зависимы.
– линейно зависимы.
3. Для  ,
, 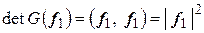 – квадрат длины вектора;
– квадрат длины вектора;
 ,
, 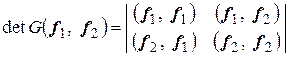 – квадрат площади;
– квадрат площади;
 ,
,  – квадрат объема;
– квадрат объема;
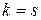 ,
, 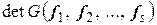 – квадрат объема
– квадрат объема  -мерного параллелепипеда, со сторонами
-мерного параллелепипеда, со сторонами 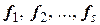 .
.
4. Процесс ортогонализации Грамма-Шмидта не меняет определитель Грамма.
Пример 7 В пространстве 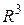 с матрицей Грамма
с матрицей Грамма 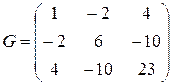 найти угол между векторами
найти угол между векторами 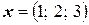 и
и 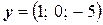 .
.
Решение. Напомним, что косинус угла между ненулевыми векторами  и
и  вычисляется по формуле:
вычисляется по формуле:
 .
.
Найдем скалярное произведение 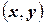 :
:
 .
.
Найдем нормы векторов  и
и  по формулам
по формулам  и
и 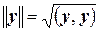 :
:
 ;
;
 .
.
Итак, 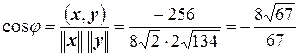 .
.
Ответ: 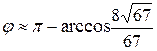 .
.
2.3 Разложение  -мерного евклидова пространства в прямую сумму подпространства и его ортогонального дополнения
-мерного евклидова пространства в прямую сумму подпространства и его ортогонального дополнения
Два подпространства  и
и 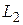 евклидова пространства называются ортогональными
евклидова пространства называются ортогональными  , если
, если 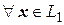 ,
,  :
: 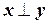 или
или 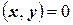 .
.
Лемма 2.1 Если  , то
, то 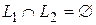 .
.
Пусть 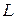 – произвольное подпространство
– произвольное подпространство  -мерного евклидова пространства Е.
-мерного евклидова пространства Е.
Совокупность  всех элементов
всех элементов  пространства Е, ортогональных к каждому элементу
пространства Е, ортогональных к каждому элементу  подпространства
подпространства 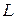 , называется ортогональным дополнением подпространства
, называется ортогональным дополнением подпространства 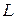 .
.
Пример 8 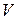 – пространство всех геометрических (свободных) векторов,
– пространство всех геометрических (свободных) векторов, 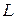 – подпространство всех векторов, параллельных некоторой плоскости;
– подпространство всех векторов, параллельных некоторой плоскости;  – подпространство всех векторов, перпендикулярных данной плоскости.
– подпространство всех векторов, перпендикулярных данной плоскости.
Пример 9 Дано подпространство  . Определить базис ортогонального дополнения
. Определить базис ортогонального дополнения  .
.
Решение. Пусть 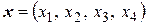 – вектор из ортогонального дополнения
– вектор из ортогонального дополнения  . Тогда
. Тогда 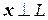 , т.е.
, т.е. 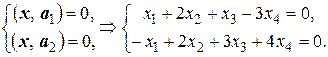 Найдем ФСР полученной системы:
Найдем ФСР полученной системы:
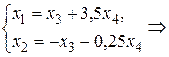
| 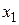
| 
| 
| 
| |
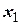
| –1 | ||||
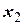
| 3,5 | –0,25 |
Векторы  и
и  образуют базис ортогонального дополнения
образуют базис ортогонального дополнения  .
.
Пусть 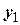 и
и  – два произвольных элемента множества
– два произвольных элемента множества  , а
, а  какой-либо элемент подпространства
какой-либо элемент подпространства 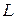 . Очевидно,
. Очевидно, 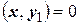 и
и  по свойству векторов множества
по свойству векторов множества  . Так как
. Так как
 ,
,
то 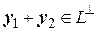 . Для произвольного числа
. Для произвольного числа  имеем
имеем  . Следовательно, и элемент
. Следовательно, и элемент 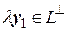 . Таким образом, множество
. Таким образом, множество  является подпространством евклидового пространства Е.
является подпространством евклидового пространства Е.
Лемма 2.2 (критерий) Пусть 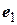 ,
, 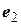 , …,
, …,  – базис в подпространстве
– базис в подпространстве  . Вектор
. Вектор 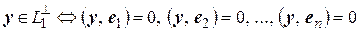 .
.
Теорема 2.5 Евклидово пространство Е есть прямая сумма произвольного подпространства 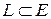 и его ортогонального дополнения
и его ортогонального дополнения  , т.е.
, т.е.  .
.
Следствие 1 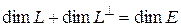 .
.
Замечание В равенстве 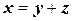 теоремы 2.4 вектор
теоремы 2.4 вектор  – ортогональная проекция вектора
– ортогональная проекция вектора  на подпространство,
на подпространство, 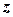 – ортогональная составляющая вектора
– ортогональная составляющая вектора  относительно подпространства.
относительно подпространства.
Пример 10 Определить проекцию вектора 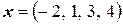 на подпространство
на подпространство 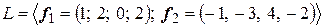 и ортогональную составляющую вектора
и ортогональную составляющую вектора  относительно подпространства
относительно подпространства 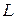 .
.
Решение.
І способ.
1) Построить ортонормированный базис данного подпространства. Координаты векторов 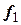 и
и  не пропорциональны, следовательно, векторы
не пропорциональны, следовательно, векторы 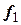 и
и  образуют базис подпространства
образуют базис подпространства 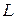 . Применим к этому базису процесс ортогонализации Грамма-Шмидта.
. Применим к этому базису процесс ортогонализации Грамма-Шмидта.
Сначала по 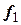 ,
,  строим ортогональный базис
строим ортогональный базис  ,
, 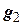 :
:
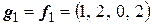 ;
;  ;
;
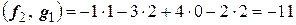 ;
;

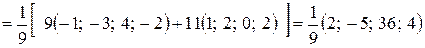
или  .
.
Как видно, 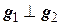 , т.к.
, т.к.  .
.
Построим теперь ортонормированный базис подпространства 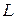 :
:
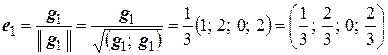 ;
;
 .
.
2) Найти скалярные произведения данного вектора  и векторов найденного базиса:
и векторов найденного базиса:
 ,
,
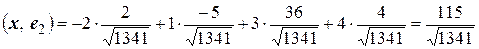 .
.
3) Найти ортогональную проекцию  вектора
вектора  на подпространство
на подпространство 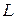 и ортогональную составляющую
и ортогональную составляющую 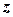 вектора
вектора  относительно подпространства
относительно подпространства 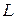 :
:
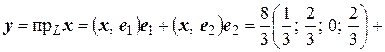

 ;
;
 .
.
ІІ способ.
1) Построить базис данного подпространства. Как было указано в первом способе данные векторы 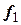 и
и  являются линейно независимыми, значит образуют базис.
являются линейно независимыми, значит образуют базис.
2) Так как по определению  , представляющий ортогональную проекцию
, представляющий ортогональную проекцию  на подпространство
на подпространство 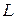 , принадлежит
, принадлежит 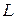 , то его можно выразить через базисные векторы этого подпространства, т.е.
, то его можно выразить через базисные векторы этого подпространства, т.е.  . Таким образом, получим
. Таким образом, получим
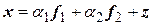 .
.
Домножим последнее равенство скалярно на 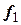 :
:
 , т.к.
, т.к. 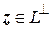 .
.
Аналогично,
 .
.
Вычислив соответствующие скалярные произведения:
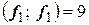 ,
, 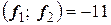 ,
, 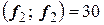 ,
, 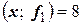 ,
,  ,
,
получим систему уравнений:
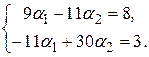
Решив систему, получим: 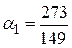 ,
, 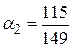 , а, значит
, а, значит
 .
.
Из равенства 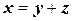 будем иметь:
будем иметь:
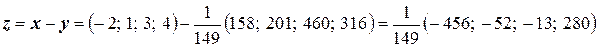 .
.
2.4 Комплексное евклидово (унитарное) пространство
Линейное пространство над полем комплексных чисел называется комплексным евклидовым пространством или унитарным, если в нём определена операция скалярного произведения двух любых векторов, т.е. указано правило, по которому каждой паре векторов  и
и  пространства ставится в соответствие комплексное число
пространства ставится в соответствие комплексное число 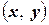 , при этом выполняются следующие условия (аксиомы скалярного произведения):
, при этом выполняются следующие условия (аксиомы скалярного произведения):
1. 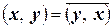
2.  .
.
3. 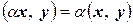 .
.
4. 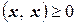 и
и  лишь при
лишь при 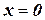 .
.
Здесь  – произвольное комплексное число;
– произвольное комплексное число; 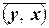 – число, сопряженное числу
– число, сопряженное числу 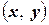 ;
;  – действительное число.
– действительное число.
Установим необходимые для дальнейшего свойства скалярного произведения.
Свойство 1 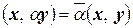 .
.
Доказательство. Согласно аксиомам 1 и 3 скалярного произведения имеем
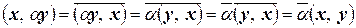 .
.
Свойство 2  .
.
Доказательство. Согласно аксиомам 1 и 2 скалярного произведения имеем
 .
.
Комплексное евклидово пространство можно сделать нормированным, если каждому вектору  поставить в соответствие действительное число
поставить в соответствие действительное число 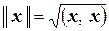 . Проверка аксиом нормы осуществляется также, как в вещественном евклидовом пространстве. Она основана на использовании неравенства Коши-Буняковского для унитарного пространства
. Проверка аксиом нормы осуществляется также, как в вещественном евклидовом пространстве. Она основана на использовании неравенства Коши-Буняковского для унитарного пространства
 .
.
Доказательство этого неравенства аналогично доказательству неравенства Коши-Буняковского для вещественного евклидова пространства.
В унитарном пространстве понятие угла между двумя векторами не определяется, однако два вектора  и
и  таких, что
таких, что 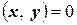 , называются ортогональными.
, называются ортогональными.
В комплексном евклидовом пространстве существуют ортонормированные базисы. Процесс ортогонализации произвольного базиса унитарного пространства в точности совпадает с описанным выше процессом ортогонализации базиса вещественного евклидова пространства.
Пусть 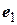 ,
, 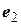 , …,
, …,  – ортонормированный базис комплексного евклидова пространства, а
– ортонормированный базис комплексного евклидова пространства, а  и
и 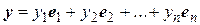 – два произвольно взятых вектора этого пространства. Тогда на основании аксиом и свойств скалярного произведения
– два произвольно взятых вектора этого пространства. Тогда на основании аксиом и свойств скалярного произведения

 ,
,
где 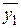 ,
, 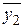 , …,
, …, 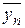 – числа, сопряженные комплексным числам
– числа, сопряженные комплексным числам  ,
, 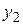 , …,
, …, 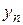 . Таким образом, скалярное произведение двух векторов унитарного пространства, в котором выбран ортонормированный базис, равно сумме произведений координат первого вектора на соответствующие сопряженные значения координат второго вектора.
. Таким образом, скалярное произведение двух векторов унитарного пространства, в котором выбран ортонормированный базис, равно сумме произведений координат первого вектора на соответствующие сопряженные значения координат второго вектора.
Date: 2015-08-24; view: 1002; Нарушение авторских прав