Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Установившееся изотермическое движение реального газа в горизонтальном трубопроводе

⇐ ПредыдущаяСтр 13 из 13

В рассматриваемом случае также справедливо уравнение Бернулли (9.1), в котором можно пренебречь членом 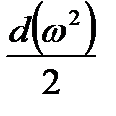, учитывающим потерь давления на изменение кине­тической энергии и которое примет вид

(9.20)

Остается в силе и уравнение неразрывности (9.2). Уравне­ние состояния будет иным

(9.21)

Тогда уравнение термодинамического процесса примет вид

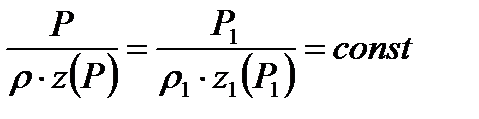(9.22)

В последнем уравнении коэффициент z, учитывающий отклонение реального газа от идеального не является постоянной величиной; он изменяется по длине газопровода в соответствии с изменением давления P.

Согласно (9.22) имеем

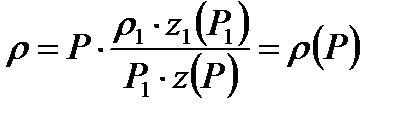(9.23)

где индексом "1", так же как и ранее, отмечены параметры в начальном сечении газопровода.

Умножая уравнение (9.20) на 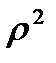и интегрируя, по­лучим

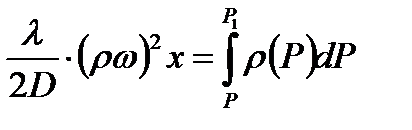(9.24)

Введем обозначение

(9.25)

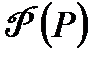- называется функцией Лейбензона.

Тогда выражение (9.24) можно переписать

(9.26)

Полагая в последнем равенстве 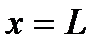и 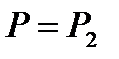, получим

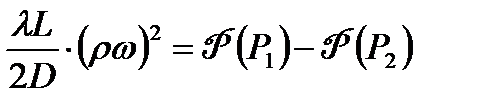(9.27)

Зная зависимость можно вычислить функцию Лей­бензона по формуле (9.25), а из (9.27) найти массовую скорость и массовый расход

Для удобства вычислений разность 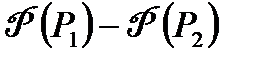представим в виде

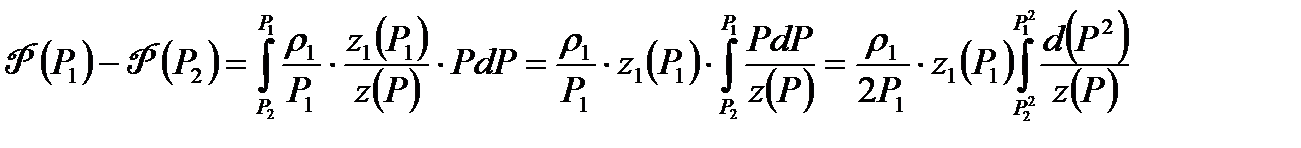(9.28)

Построим зависимость 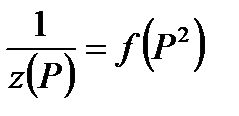как показано на рис. 9.3

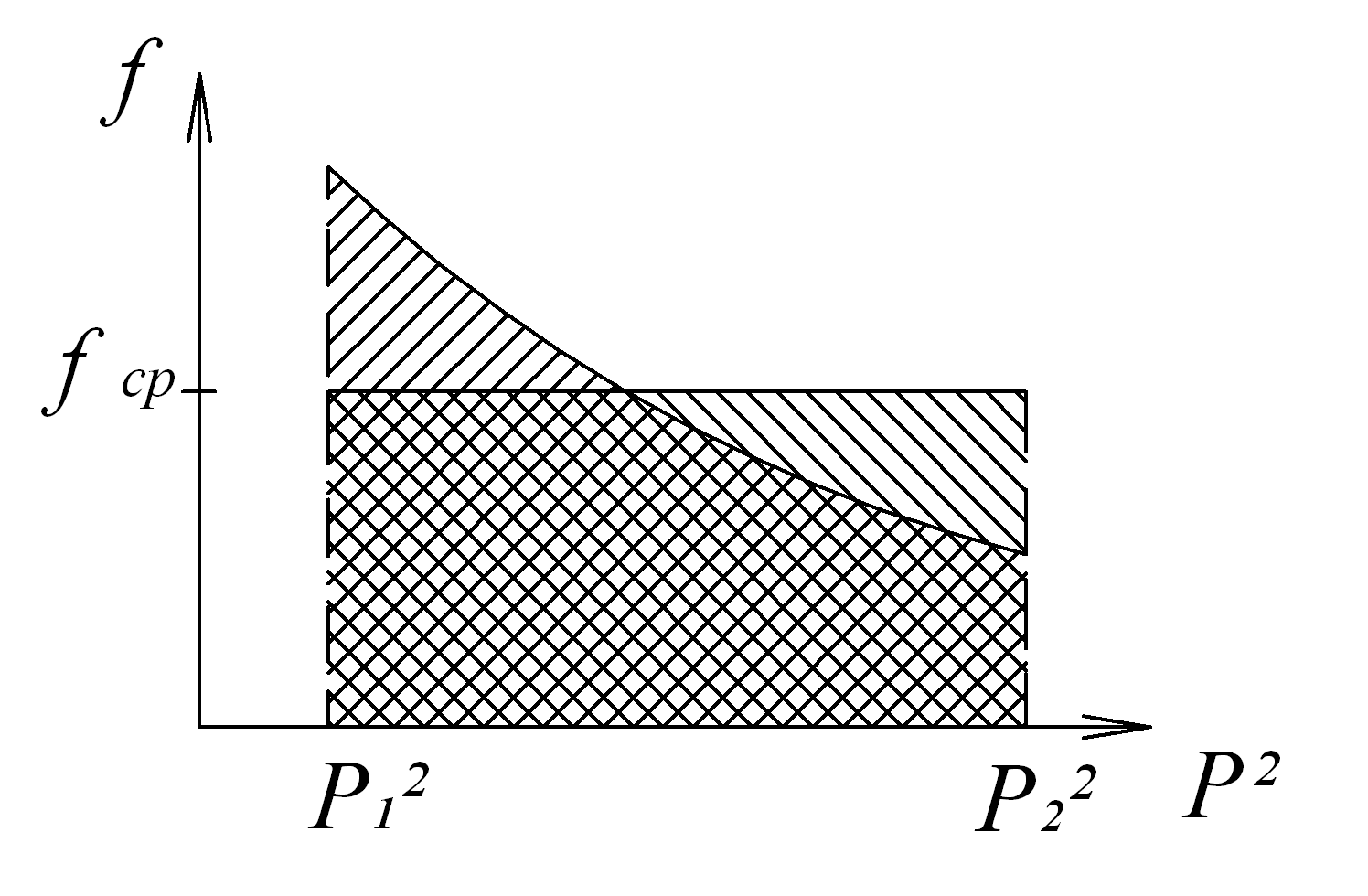
Рис. 9.3. К вычислению среднего значения функции 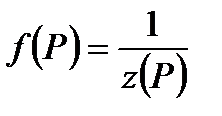в газопроводе

 

 

Интеграл

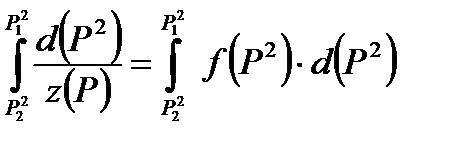
можно вычислить графически как площадь, заключенная кривой 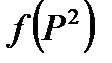. Если ввести среднее значение 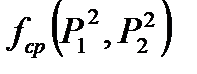- высота прямоугольника, равновеликой площади, тогда

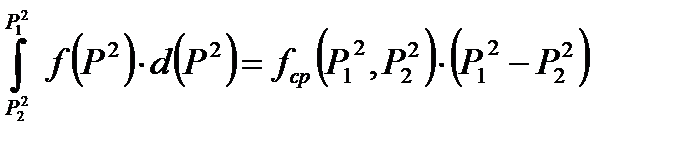(9.29)

Значение 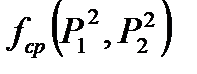находится графическим путем. Тогда согласно изложенному массовая скорость нахо­дится из (9.27)

 

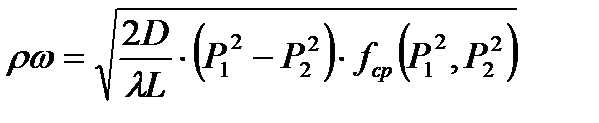(9.30)

 


ПРИЛОЖЕНИЕ

Таблица газодинамических функций

           

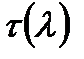
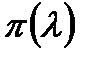
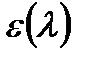
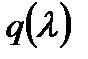
показатель адиабаты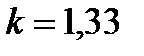

0,00 1,0000 1,0000 1,0000 0,0000 0,0000
0,10 0,9986 0,9944 0,9958 0,1582 0,0927
0,20 0,9943 0,9774 0,9830 0,3123 0,1858
0,30 0,9873 0,9496 0,9619 0,4584 0,2797
0,40 0,9773 0,9118 0,9329 0,5928 0,3749
0,50 0,9646 0,8648 0,8966 0,7121 0,4717
0,60 0,9490 0,8098 0,8533 0,8133 0,5706
0,70 0,9306 0,7483 0,8041 0,8941 0,6723
0,80 0,9094 0,6819 0,7499 0,9529 0,7772
0,90 0,8853 0,6120 0,6913 0,9883 0,8862
1,00 0,8584 0,5404 0,6296 1,0000 1,0000
1,10 0,8286 0,4688 0,5658 0,9886 1,1196
1,20 0,7961 0,3986 0,5007 0,9545 1,2461
1,30 0,7606 0,3320 0,4365 0,9014 1,3820
1,40 0,7224 0,2697 0,3733 0,8303 1,5290
1,50 0,6813 0,2138 0,3126 0,7449 1,6836
1,60 0,6374 0,1628 0,2554 0,6492 1,8567
1,70 0,5907 0,1198 0,2029 0,5478 2,0493
1,80 0,5411 0,0842 0,1555 0,4447 2,2670
1,90 0,4887 0,0558 0,1142 0,3447 2,5180
2,00 0,4335 0,0344 0,0794 0,2523 2,8143
2,10 0,3754 0,0193 0,0514 0,1713 3,1754
2,20 0,3145 0,0094 0,0300 0,1050 3,6344
2,30 0,2508 0,0038 0,0151 0,0553 4,2551
2,40 0,1842 0,0011 0,0059 0,0226 5,1807
2,50 0,1148 0,0002 0,0014 0,0050 6,8355
2,60 0,0426 0,299.10-5 0,702.10-4 0,0003 11,6736
2,657          

показатель адиабаты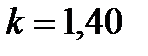

           
0,00 1,0000 1,0000 1,0000 0,0000 0,0000
0,10 0,9983 0,9942 0,9959 0,1580 0,0914
0,20 0,9933 0,9768 0,9834 0,3102 0,1830
0,30 0,9850 0,9485 0,9630 0,4557 0,2760
0,40 0,9733 0,9097 0,9346 0,5897 0,3701
0,50 0,9583 0,8616 0,8991 0,7021 0,4663
0,60 0,9400 0,8053 0,8567 0,8109 0,5649
0,70 0,9183 0,7422 0,8082 0,8924 0,6668
0,80 0,8933 0,6738 0,7543 0,9518 0,7727
0,90 0,8650 0,6019 0,6959 0,9879 0,8833
1,00 0,8333 0,5283 0,6340 1,0000 1,0000
1,10 0,7983 0,4546 0,5694 0,9880 1,1239
1,20 0,7600 0,3827 0,5035 0,9531 1,2566
1,30 0,7183 0,3142 0,4374 0,8969 1,4002
1,40 0,6733 0,2505 0,3720 0,8216 1,5575
1,50 0,6250 0,1930 0,3088 0,7307 1,7321
1,60 0,5733 0,1427 0,2489 0,6282 1,9290
1,70 0,5183 0,1003 0,1934 0,5187 2,1555
1,80 0,4600 0,0660 0,1435 0,4075 2,4227
1,90 0,3983 0,0399 0,1002 0,3002 2,7481
2,00 0,3333 0,0214 0,0642 0,2024 3,1622
2,10 0,2650 0,0096 0,0361 0,1198 3,7240
2,20 0,1933 0,0032 0,0164 0,0570 4,5674
2,30 0,1183 0,0006 0,0048 0,0175 6,1033
2,40 0,0400 0,128 .10-4 0,32 .10-3 0,0012 10,957
2,449          

 


СОДЕРЖАНИЕ

ВВЕДЕНИЕ 3

1. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ КУРСОВ ФИЗИКИ И ТЕРМОДИНАМИКИ 4

1.1. Основные свойства газа 4

1.2.Основные сведения из термодинамики 6

2. ОСНОВНЫЕ ЗАКОНЫ ДВИЖЕНИЯ СЖИМАЕМОЙ СРЕДЫ 9

2.1. Вводные замечания 9

2.2. Закон сохранения массы 9

2.3. Закон изменения количества движения 11

2.4. Закон изменения момента количества движения 12

2.5. Закон сохранения энергии 14

2.6. Уравнения Бернулли-Сен Венана. Параметры заторможенного газа 16

3. ЧИСЛО МАХА. РЕЖИМЫ ТЕЧЕНИЯ ГАЗА 18

4. СВЯЗЬ МЕЖДУ ПЛОЩАДЬЮ СЕЧЕНИЯ И СКОРОСТЬЮ ПОТОКА.

СОПЛО ЛАВАЛЯ 21

5. ИСТЕЧЕНИЕ ГАЗА ИЗ РЕЗЕРВУАРА ЧЕРЕЗ СХОДЯЩУ27ЮСЯ НАСАДКУ 23

6. РЕЖИМЫ РАБОТЫ СОПЛА ЛАВАЛЯ 27

7. КРИТЕРИИ ПОДОБИЯ. ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ 30

8. СКАЧКИ УПЛОТНЕНИЯ 34

8.1. Скорость распространения волны сжатия 34

8.2. Прямой скачок уплотнения 36

8.3. Косой скачок уплотнения 40

9. ОСНОВНЫЕ ЗАДАЧИ УСТАГОВИВШЕГОСЯ ДВИЖЕНИЯ ГАЗА В ТРУБАХ 42

9.1. Изотермическое движение идеального газа в горизонтальном трубопроводе 42

9.2. Установившееся изотермическое движение реального газа в горизонтальном трубопроводе 46

ПРИЛОЖЕНИЕ 49

 

 


⇐ Предыдущая45678910111213





Date: 2015-08-15; view: 567; Нарушение авторских прав


mydocx.ru - 2015-2024 year. (0.016 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию