Уравнение Бернулли - Сен Венана. Параметры заторможенного газа

Часто в инженерной практике приходится иметь дело с частными формами уравнения энергии. Например, в большинстве случаев изменение потенциальной энергии положения пренебре­жимо мало по сравнению с другими членами уравнения (2.20), поэтому членом 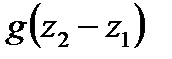пренебрегают. Если еще отсутст­вуют техническая работа () и теплообмен с окружаю­щей средой , т.е. в случае энергетически изоли­рованного движения газа уравнение (2.20) принимает вид

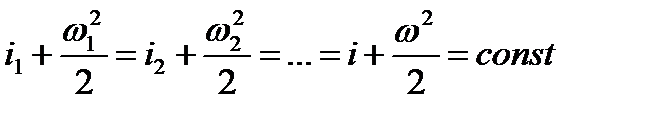(2.23)

которое в газодинамике называют уравнением Бернулли - Сен Венана. Строго говоря, оно справедливо лишь для горизонталь­ного или невесомого энергетически изолированного потока газа.

Используя выражения (1.17) и (1.18) для энтальпии, можно уравнению Бернулли-Сен Венана (2.23) придать следую­щие формы записи:

(2.24)

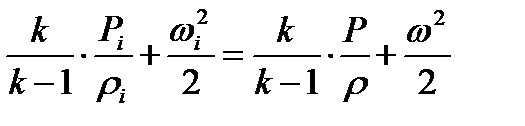(2.25)

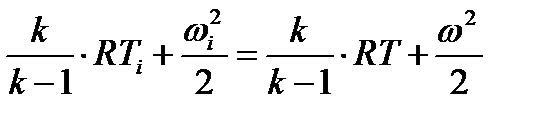(2.26)

Уравнение Бернулли - Сен Венана позволяет ввести ряд важных понятий, так называемых параметров торможения. Если газовый поток, имевший скорость 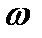при энтальпии затормозить в условиях энергетической изоляции, т.е. сни­зить скорость до 0, то энтальпия газа повысится до макси­мального значения 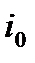, определяемого, согласно (2.23),равенством

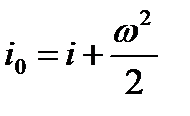(2.27)

Величина 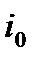носит название полной энтальпии движуще­гося газа.

При энергетически изолированном торможения газ прини­мает температуру Т₀, определяемую, согласно (1.17), по формуле

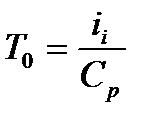(2.28)

которая называется температурой торможения. Используя (2.24), можно для вычисления получить иное выраже­ние

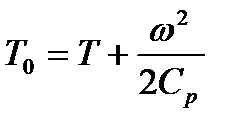(2.29)

Аналогичным образом вводятся понятия давления торможения 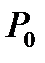и плотность торможения 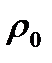, которые связаны соот­ношением, вытекающим из (2.25)

(2.30)

Давление торможения 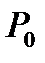называют также полным дав­лением.

Для идеального (невязкого) газа при отсутствии энер­гообмена потока с внешней средой параметры торможения газа вдоль потока не изменяются.

В реальных условиях, т.е. для вязкого газа, а также при энергообмене потока газа с окружающей средой параметры торможения от сечения к сечению вдоль потока изменяются.

Из выражений (2.27) - (2.30) следует, что скорость потока газа может увеличиваться, но не беспредельно. Макси­мально возможную скорость газ может достичь (теоретически) при (или 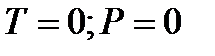). В соответствии с (2.27) - (2.30) максимальная скорость 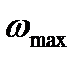может быть выражена через параметры торможения

(2.31)

Из (2.31) следует, что увеличение максимального значения скорости может быть достигнуто только повышением температуры торможения (т.е. полного теплосодержания).

3. ЧИСЛО МАХА. РЕЖИМЫ ТЕЧЕНИЯ ГАЗА

Чтобы газ из состояния покоя пришел в движение со скоростью , необходимо, согласно (2.27), израсходовать часть его энтальпии, равную

(3.1)

Разделив обе части равенства (3.1) на энтальпию га­зового потока, получим с учетом (1.17) равенство в без­размерной форме

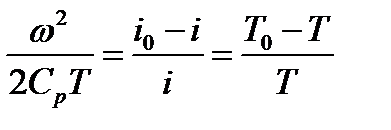(3.2)

над которым проведем дальнейшие преобразования. Для этого умножим и разделим левую часть равенства (3.2) на газовую постоянную R. Тогда с учетом формулы Майера (1.16) и выражения для показателя адиабаты (1.19) указанное равен­ство примет вид

(3.3)

Из курса физики известно, что в сжимаемой среде звук распространяется со скоростью, определяемой

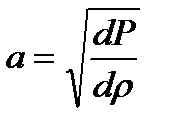(3.4)

Обычно распространение звука сопровождается столь не­значительным изменением состояния газа, что энтропию можно считать постоянной. Тогда воспользовавшись уравнением изоэнтропийного процесса (1.21), получим

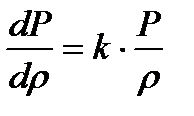
которое для идеального газа равносильно

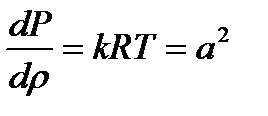(3.5)

С учетом выражений (3.3), (3.4) и (3.5) равенст­во (3.2) можно представить в виде

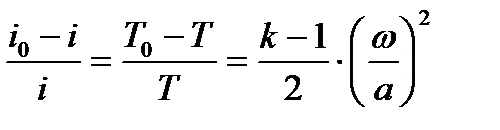(3.6)

т.е. интересующая нас степень преобразования полной энталь­пии движущегося газа в кинетическую энергию определяется отношением скорости потока газа к местной скорости звука. Под словом "местная" подчеркивается, что скорость звука бе­рется в конкретном сечении газового потока. В общем случае скорость звука при переходе от одного сечения потока к другому меняется в соответствии с изменениями параметров состояния газа.

Отношение скорости потока к местной скорости звука в потоке принято называть числом Маха и обозначать буквой

(3.7)

Число Маха является основным критерием подобия газовых потоков большой скорости. При одинаковых значениях числа 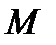потоки считаются подобными с газодинамической точки зрения.

Из выражения (3.6) можно получить расчетную формулу для отношения температуры торможения к температуре потока как функцию числа Маха

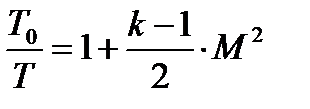(3.8)

Из (3,8) видно, что число принимает максимальное значение_, равное бесконечности, при . Минимальное значение 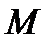, равное 0, соответствует, согласно (3.7), случаю покоя газа ().

Течение газа называется дозвуковым, если скорость потока меньше скорости звука, т.е., когда .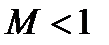

Если , т.е. когда , течение газа назы­ваемся сверхзвуковым.

При 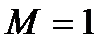режим течения газа называется критическим, а соответствующая ему скорость 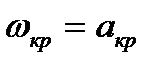- критической. Да и все параметры потока газа, характеризующие критический режим течения, называются критическими.

Из формулы (3.8) можно получить выражение для вычисле­ния критической температуры, подставив в нее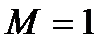

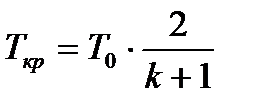(3.9)

Получим выражение для вычисления оптической скорости. Для этого подставим в (3.5) значение , определяе­мое, согласно (3.9),

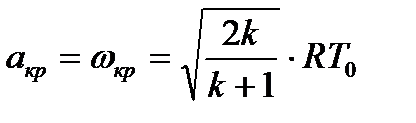(3.10)

Прежде чем найти выражения для критического давления и критической плотности 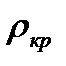, установим зависимости давления и плотности 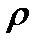от параметров торможений и числа Маха. Согласно уравнению Клапейрона-Менделеева (1.3), можно записать для двух состояний газа

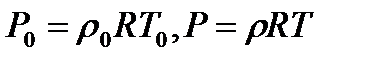
Почленное деление этих равенств дает

(3.11)

В случае изоэнтропического процесса, согласно (1.21), имеем

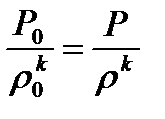
отсюда следует

(3.12)

Приравнивая правые части равенств (3.11) и (3.12), получим с учетом (3.8) следующее соотношение

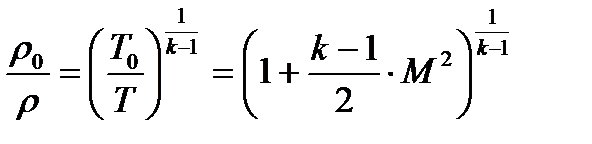(3.13)

Подставляя в (3.12) выражение (3.13), имеем

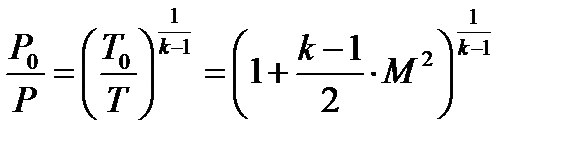(3.14)

Следует отметить, что если параметры торможения 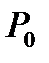, , 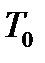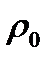берутся в одном и том же сечении, что 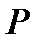, , то формулы (3.13) и (3.14) справедливы всегда, в том числе и при неадиабатических течениях газа. Если же парамет­ры торможения берутся в одном сечении потока, а величины 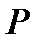, , - в другом, то формулы (3.13) и (3.14) справед­ливы только для случая изоэнтропического течения газа.

Полагая в формулах (3.13) и (3.14) 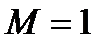, получим искомые выражения для критических значений плотности и дав­ления

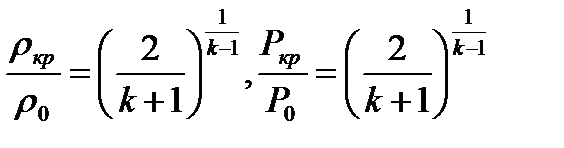(3.15)

Следует обратить внимание, что параметры 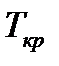и ,

характеризующие критический режим течения газа не следует смешивать с критическими температурой и давлением ( и 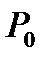), являющимися физическими характеристиками газа [формулу (1.7)].

При переходе через критический режим течения газа происходят существенные качественные изменения, что является одним из наглядных примеров проявления всеобщего закона диалекти­ческого материализма - закона перехода количества в качество. Так при переходе через критический режим качественным образом изменяется соотношение между площадью сечения газового потока и его скоростью; при сверхзвуковом течении газа возникает вол­новое сопротивление, не существующее при дозвуковом течении и т.п.

4. СВЯЗЬ МЕЖДУ ПЛОЩАДЬЮ СЕЧЕНИЯ И СКОРОСТЬЮ ПОТОКА ГАЗА. СОПЛО ЛАВАЛЯ

Для установления связи между площадью сечения 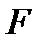и скоростью потока рассмотрим случай горизонтального энер­гетически изолированного течения газа в канале переменного сечения. Воспользуемся уравнением расхода для установившего­ся движения в форме (2.5). Продифференцировав это уравне­ние как произведение трех переменных величин, получим

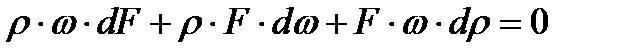
Разделим это уравнение на массовый расход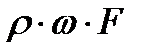

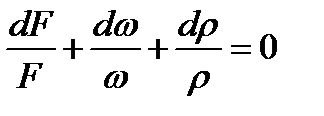
Отсюда находим относительно изменение площади сечения потока

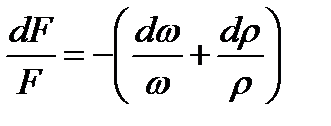(4.1)

Чтобы получить искомую зависимость, необходимо в выражении (4.1) выразить член через скорость . Для этого воспользуемся уравнением Бернулли (2.22), которое для рассматриваемого случая (потерями давления на гидравли­ческие сопротивления пренебрегаем) примет вид

или иначе еще

Решая последнее равенство относительно и учитывая определение местной скорости звука и числа Маха, согласно (3.4) и (3.7), имеем

С учетом этого равенства можно представить выражение (4.1) к окончательному виду

(4.2)

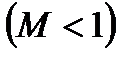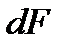которое позволяет провести качественный анализ влияния пло­щади сечения потока на величину его скорости. Выражение , стоящее в правой части равенства (4.3), может принимать как положительное, так и отрицательное значения в зависимости от значения числа Маха. Так, при дозвуковом те­чении газа и, следовательно, . Поэтому, согласно (4.3) и 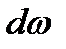, должны иметь разные знаки. Это равносильно тому, что при дозвуковом течении увеличение площади сечения () ведет к уменьшению скорости по­тока газа (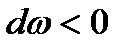). И наоборот, уменьшение площади сече­ния () приводит к увеличению скорости газа ()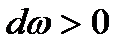

При сверхзвуковом течении газа 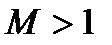и 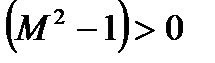. Тогда, согласно (4.3), 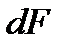и 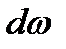имеют одинаковый знак. Следовательно, при сверхзвуковом течении газа увеличение площади сечения потока () приводит к дальнейшему увеличению скорости (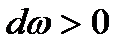). И наоборот, уменьшение пло­щади сечения () влечет уменьшение скорости потока газа ()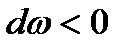

Установленное свойство геометрического воздействия на поток газа позволяет спроектировать сопло, которое преобра­зует дозвуковое течение газа в сверхзвуковое, и называется соплом Лаваля (рис. 4.1). Оно состоит из сужающей (дозву­ковой) и расширяющейся (сверхзвуковой) частей. В самом узком сечении сверхзвукового сопла скорость потока должна достигать критического значения, равного скорости звука.

Рис. 4.1 Сопло Лаваля

Сопло Лаваля по форме напоминает трубу Вентури, при­меняемую для измерения расхода маловязкой капельной жидкости. Для избежания отрыва газовой струи конусность расширяющейся части (диффузора) сопла не должна превышать 8-12°.

5. ИСТЕЧЕНИЕ ГАЗА ИЗ РЕЗЕРВУАРА ЧЕРЕЗ СХОДЯЩУЮСЯ НАСАДКУ

Рассмотрим установившееся истечение газа из резервуара с большим давлением через сходящуюся насадку (рис 5.1).

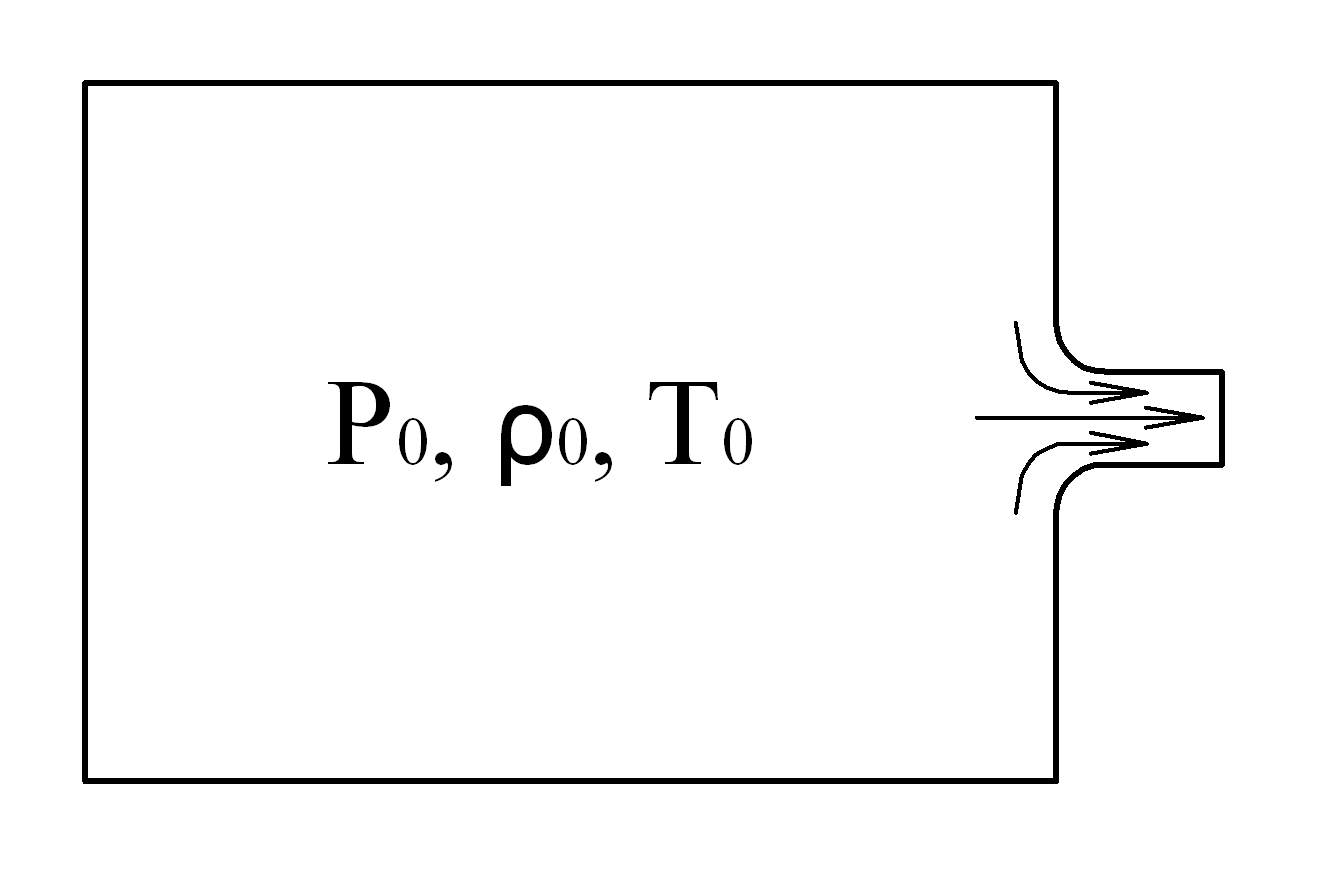
Рис. 5.1. Схема истечения газа из ре­зервуара через сходящуюся насадку

Пусть размеры резервуара достаточно велики, чтобы пре­небречь скоростью газа внутри резервуара, т.е. можно считать, что газ в резервуаре покоится. Обозначим через , площадь выходного сечения насадки, а скорость в давление в этом сечении, соответственно, через и .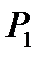

Установим зависимость массового расхода газа от внеш­него давления , т.е. от давления среды, в которую истекает газ. Забегая вперед, отметим, что возможны случаи, когда давление в выходном сечении насадки 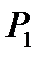равно давле­нию внешней среды и когда 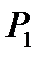отличается от . В дальнейшем этому явлению будет дано физическое объяснение.

Для получения искомой зависимости предположим, что ис­течение происходит настолько быстро, что теплообменом с окружающей средой и трением газа можно пренебречь. Это равно­сильно тому, что процесс изменения состояния газа при исте­чении через насадку - изоэнтропический. Тогда параметры торможения в любом сечении насадки неизменны и соответству­ют параметрам состояния газа в резервуаре 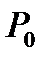, , 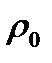. Для изоэнтропического процесса, согласно (1.21), можно записать соотношение

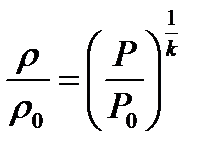(5.1)

Для рассматриваемого течения газа справедливо уравне­ние Бернулли-Сен Венана, которое используем в форм. (2.25) для двух сечений: одно в резервуаре на достаточном удалении от насадки (где скорость движения равна нулю), другое - произвольное сечение в самой насадке.

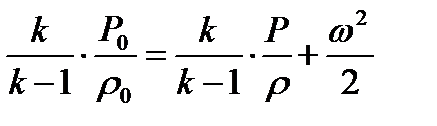(5.2)

Решая это уравнение относительно скорости газа 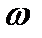, с учетом соотношения (5.1) получим

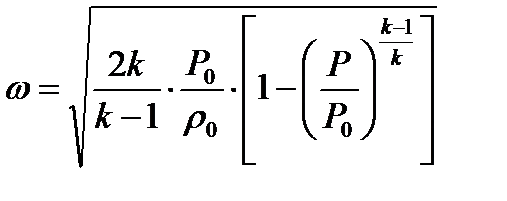(5.3)

Поскольку движение установившееся, массовый расход га­за 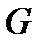в любом сечении насадки одинаковый, равный

(5.4)

Запишем последнее выражение дня сечения на выходе из насадки. Для этого достаточно заменить в нем на и на

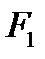
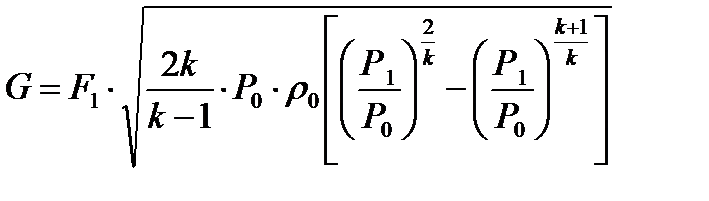(5.5)

Выражение (5.5) и является искомой зависимостью 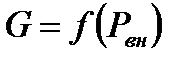. При этом пока (до выяснения физической сущности) будем считать, что . Проанализируем полученное выражение (5.5). В частности, найдем значение , при котором 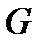достигает максимального значения.

Для удобства введем обозначение 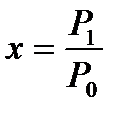. Рассмотрим функцию, заключенную в квадратных скобках выражения (5.5), которая с учетом принятого обозначения имеет вид

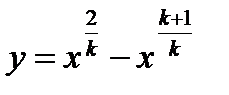(5.6)

Эта функция дважды обращается в нуль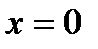: при и при , следовательно, в интервале [0,1] она имеет экстре­мум. Для отыскания экстремума необходимо приравнять нулю первую производную

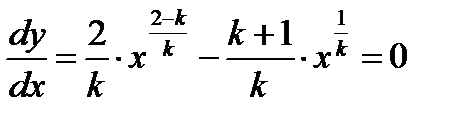
Решая полученное уравнение относительно , получим

(5.7)

следовательно, при значении

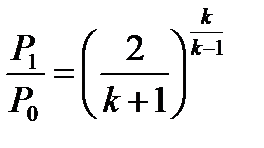(5.8)

массовый расход газа через сходящуюся насадку достигает эк­стремального значения. Можно показать, что это максимум. Сравнивая (5.8) с выражением (3.15), видим, что 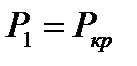. Следовательно, массовый расход 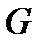достигает максимума при .Значение 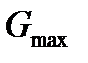может быть найдено либо по формуле (5.5) подстановкой в него , либо по формуле . Подставляя сюда значения и 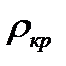по формулам (3.10) и (3.15), получим окончательно выра­жение

(5.9)

Таким образом, согласно формулы (5.5), массовый рас­ход газа через сходящуюся насадку с уменьшением давления (правая ветвь кривой на рис. 5.2) возрастает до тех пор, пока не станет равным критическому 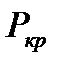, а скорость газа при этом достигнет звуковой, т.е. . Дальнейшее снижение внешнего давления в соответствии с фор­мулой (5.8) должно приводить к уменьшению массового рас­хода (левая ветвь ОА кривой на рис. 5.2, показанная пунк­тиром). Однако опыт показывает, что при изменении внешнего давления в диапазоне массовый расход газа через сходящуюся насадку остается постоянным, равным максимальному значению, определяемому формулой (5.9). При этом давление газовой струи на выходе из насадки остается неизменным, равным 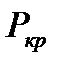, т.е. между и возникает разрыв. Такому явлению можно дать следующее физическое тол­кование.

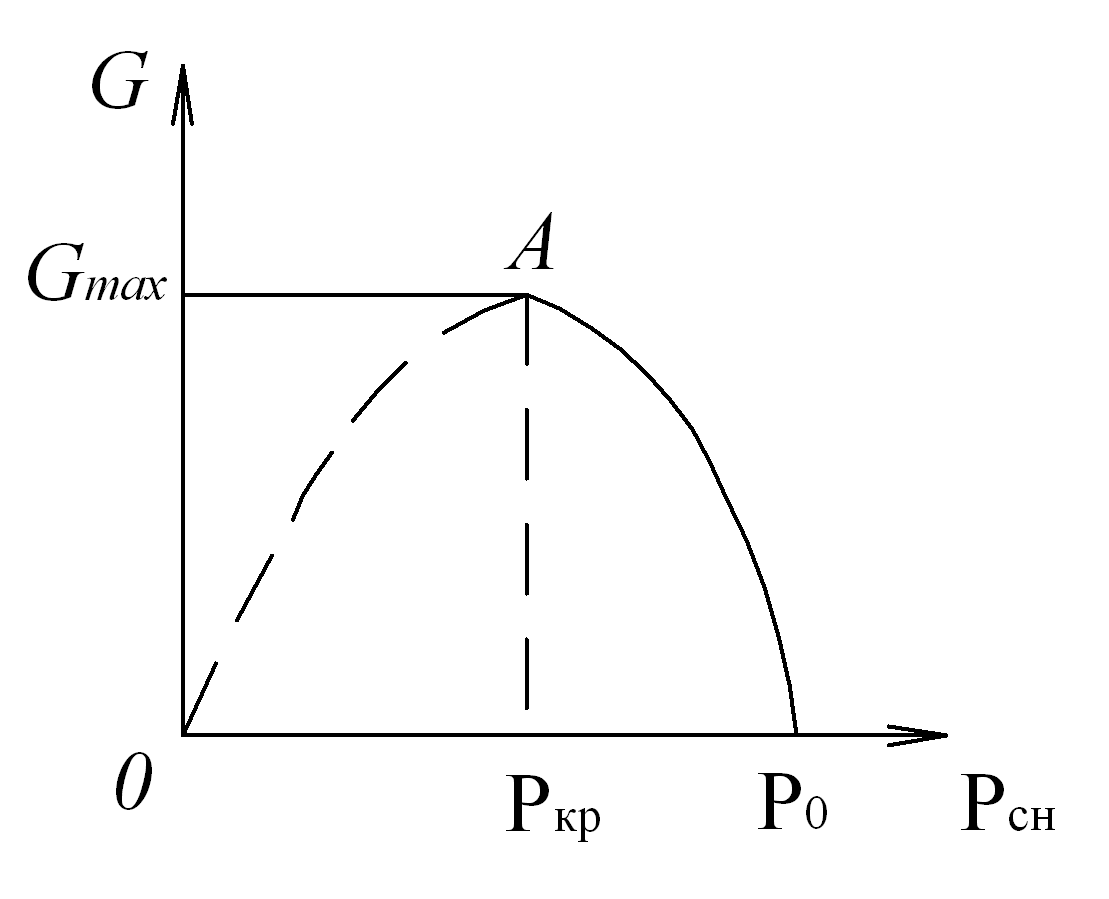
Рис. 5.2 Зависимость массового расхода rasa от внеш­него давления (среды) при истечении через сходящуюся насадку

Пунктирная ветвь кривой на рис. 5.2 может быть реали­зована только при сверхзвуковом течении. Получить такое те­чение с помощью сходящейся насадки невозможно. Для перехода к сверхзвуковым скоростям необходимы специальные условия, а именно, чтобы площадь сечения газового потока после достиже­ния звуковой скорости увеличивалась (см. свойства сверх­звуковых и дозвуковых потоков). Поэтому выражение (5.5) для массового расхода газа при истечении через сходящуюся насадку имеет физический смысл только при 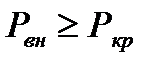(область дозвукового течения). Именно в этой области выполняется равенство 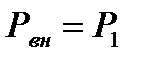. При скорости газа в конце насадки, равной скорости звука, изменение возмущений (давления) во внешней среде не может проникнуть через насадку, так как оно будет сносится струей газа со скоростью звука (с такой же скоростью распространяются и малые возмущения). Созда­ется барьер, который и объясняет наличие скачка давлений (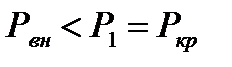) при звуковой скорости истечения газа.

Параметры потока изменяются: давление, температура, плотность и скорость газа, изменяются вдоль насадки. Для изменения давления можно получить выражение, если прирав­нять массовые расходы по формулам (5.4) и (5.5)

(5.10)

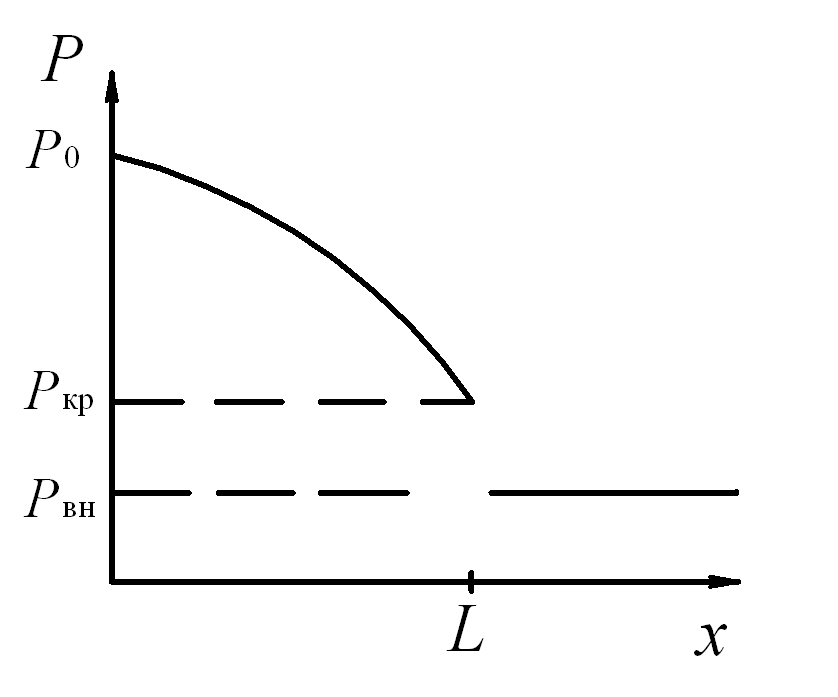Изменение давления газа при истечения через сходящуюся насадку со звуковой скоростью для случая 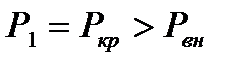можно представить графически (рис. 5.3)

Рис. 5.3. Изменение давления в потоке газа при исте­чении через сходящую­ся насадку

Из рис. 5.3 видно, что вдоль сходящейся насадки давле­ние плавно снижается до значения 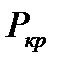( 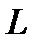- длина насадки). На выходе из насадки давление в газе претерпевает скачок до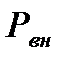

6. РЕЖИМЫ РАБОТЫ СОПЛА ЛАВАЛЯ

Как отмечалось в п. 4, сопло Лаваля служит для получе­ния сверхзвуковых потоков газа. Конфигурация сопла должна обеспечивать скорость газа в горловине, равную критической (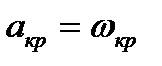). Обозначим через - площадь горловины сопла. Для получения на выходе из сопла сверхзвукового по­тока газа с определенным значением числа Маха необходи­мо соответствующим образом подобрать площадь этого сече­ния 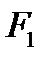. Число 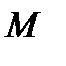вдоль сопла непрерывно изменяется. Установим зависимость площади сечения сопла как функцию числа . Для этого воспользуемся уравнением расхода (для установившегося движения).

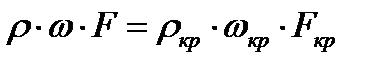(6.1)

где F - площадь произвольного сечения сопла.

Отсюда

(6.2)

Заменяя в нем и , получим

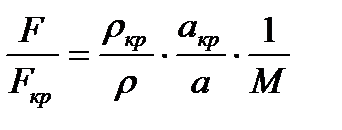(6.3)

Используя выражения (1.3, (2.21) и (3.5), можно получить соотношения

(6.4)

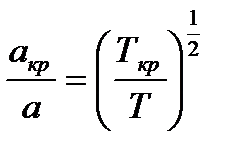(6.5)

Из выражений (3.8) и (3.9) следует

(6.6)

Подставляя (6.4), (6.5) и (6.6) в (6.3), полу­чим искомую зависимость в виде

(6.7)

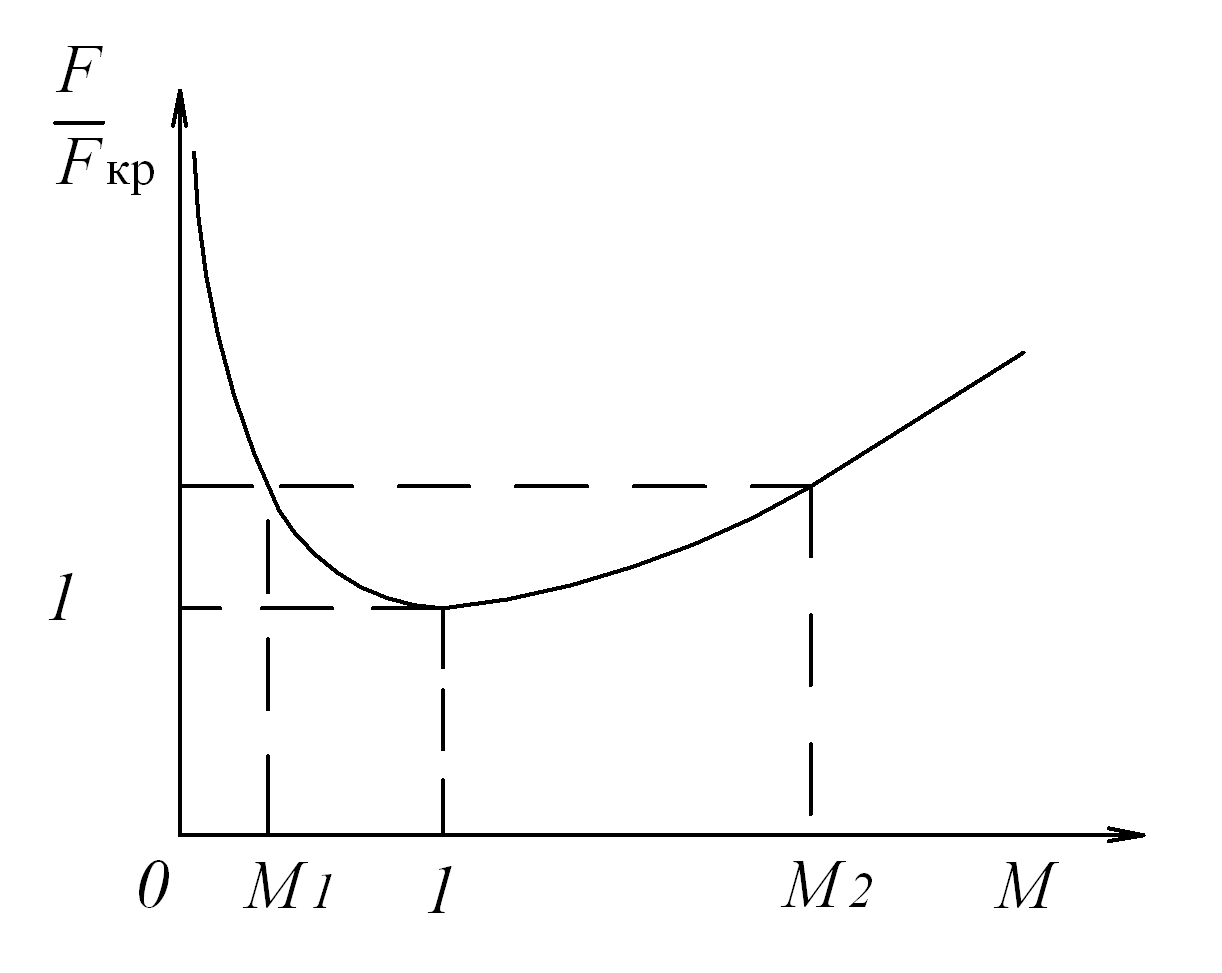которая представлена графически на рис. (6.1)

Рис. 6.1. График изменения площади сечения потока газа от числа Маха

Из графика рис. 6.1 видно, что одному и тому же значе­нию 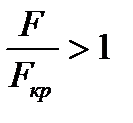отвечают два значения числа : одно соответствует дозвуковому течению, другое - сверхзву­ковому.

Изменение температуры, плотности и давления вдоль соп­ла Лаваля будут изменяться в соответствии с формулами (3.8), (3.13) и (3.14), если, конечно, движение адиабатическое.

На основании формулы (3.14) можно сделать вывод, что для получения сверхзвукового потока с заданным числом 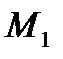необходимо, чтобы между давлением в резервуаре (равное давлению торможения), к котором подсоединено сопло, и давлением на выходе из сопла существовало определенное соот­ношение.

Режим работы сопла Лаваля, соответствующий рассмотрен­ному выше случаю, называется расчетным. Этот режим характе­рен тем, что на всем протяжении сопла происходит адиабати­ческое расширение газа. В конфузорной части происходит ускорение дозвукового потока, в горловине этот поток становит­ся звуковым, в диффузорной части - сверхзвуковым. На выходе сопла устанавливается давление , которое легко под­считать по формулам (3.14) и (6.7), полагая в них и . 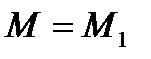График изменения давления вдоль сопла при расчетном режиме представлен на рис. 6.2 кривыми 1 и 5.

Массовый расход газа при расчетном режиме соответст­вует максимальному значению и определяется по формуле

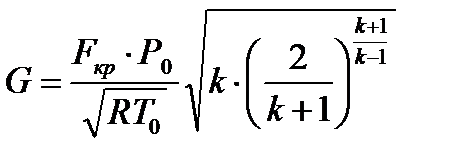(6.8)

которая получается из (формулы (5.9) заменой 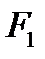на - площадь сечения горловины сопла.

Так же как и при истечении через насадку будем различать давление на выходе из сопла 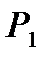и давление внеш­ней среды, куда истекает газ, и обозначать соответственно через 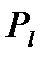и .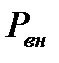

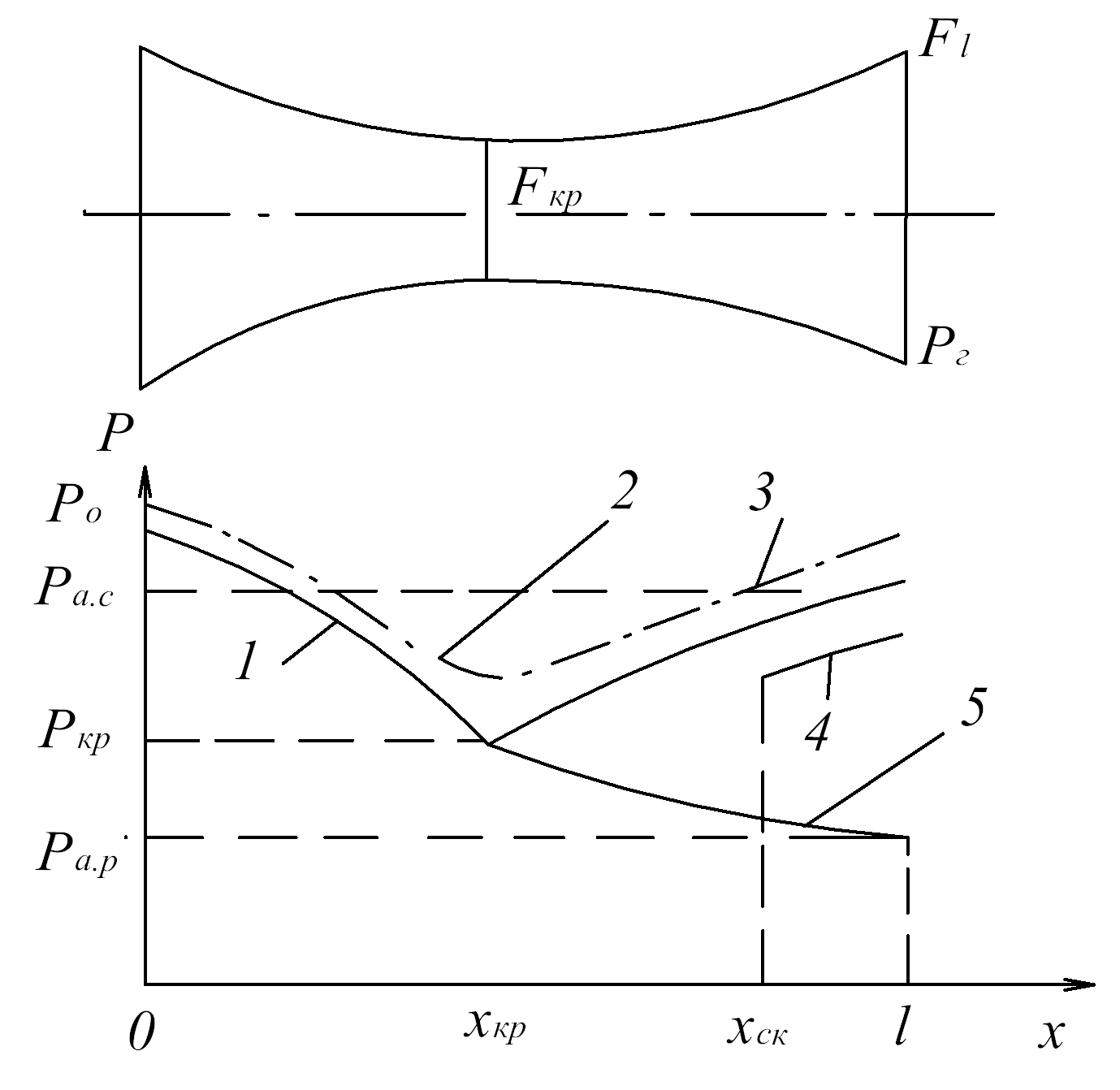
Рис. 6.2. Графики изменения дав­ления в сопле Лаваля при различных режимах его работы

Расчетный режим работы сопла Лаваля может быть реали­зован лишь при выполнении условия: . Если это условие не выполняется, то сопло будет работать на од­ном из нерасчетных режимов.

Следует обратить внимание изучающего на многообразие и сложность течения газа в сопле Лаваля. Не все режимы под­даются чисто теоретическому изучению и требуют эксперимен­тальных исследований.

Анализ эмпирических данных позволяет разбить все многообразие нерасчетных режимов работы сопла Лаваля на четыре характерные группы, в пределах каждой из которых картина течения газа качественно сохраняется. Реализация той или иной группы режимов зависит от численного значения внешнего дав­ления.

1 группа: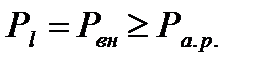

2 группа: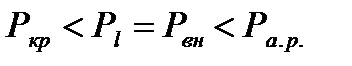

3 группа:

4 группа:

Общим для всех групп является то, что движение в конфузорной части дозвуковое, адиабатическое и поддается рас­чету по выше приведенным формулам для сходящейся насадки. Различие наблюдается только в диффузорной части сопла.

Характерным для первой группы режимов является дозвуковое течение в диффузорной части. В этой части сопла происходит замедление газового потока с одновременным повышением давления по адиабате Пуассона до значения (давление адиабатического сжатия). Характер изменения давления пред­ставлен на рис. 6.2 штрихпунктирной кривой 2. Вычисление массового расхода газа для этой группы режимов можно выпол­нять по формуле (5.5), в которой следует изложить и 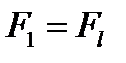Снижение давления 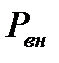приводит к увеличе­нию массового расхода. Максимального значения он может до­стигнуть, когда 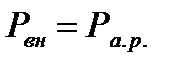, при этом в горловине сопла параметры потока достигнут критических значений. Из­менение давления, соответствующее этому предельному значе­нию показано кривыми 1 и 3 на рис. 6.2.

Для второй, третьей и четвертой групп нерасчетных ре­жимов, так же как и для расчетного режима давление в конфузорной части изменяется по кривой 1 на рис. 6.2. Харак­терных для второй и третьей групп является наличие в диффузорной части сопла так называемых скачков уплотнения. Фронт скачка характеризуется координатой 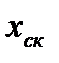(рис. 6.2), давление до скачка уплотнения изменяется по кривой 5, а за скачком - по кривой 4. В сечении сопла, определяемом коор­динатой 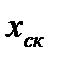существует одновременно два значения давле­ния. С понижением внешнего давления положение фронта скачка смещается в направлении к выходному сечению сопла.

Поток газа на выходе из сопла при нерасчетных режимах 2 группы дозвуковой , а 3 группы - сверхзвуко­вой .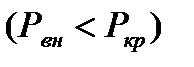

При (4 группа режимов) картина течения газа внутри сопла не отличается от таковой при расчетном режиме и давление изменяется в соответствии с кривыми 1 и 5 (рис. 6.2). По выходе из сопла в свободной сверхзвуковой струе образуется система волн расширения, посредством кото­рых происходит снижение давления от до

7. КРИТЕРИИ ПОДОБИЯ. ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ

В газодинамике кроме числа Маха 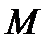вводят еще два кри­терия подобия: коэффициент скорости 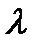по формуле

(7.1)

и безразмерная скорость

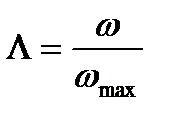(7.2)

где - скорость газа в интересующем сечении потока, и соответственно критическая и максимально возможная скорость газа в том же сечении. Значения и определяются формулами (3.10) и (2.31).

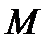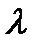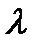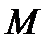Следует отметить, что вводимые критерии подобия газово­го потока , и взаимосвязаны и взаимозаменяемы. Можно выразить каждый из них через другой. Найдем связь меж­ду и . Для этого, воспользовавшись (7.1), прове­дем следующие преобразования

(7.3)

Первый сомножитель в правой части (7.3) представляет собой 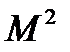. Найдем два других сомножителя. Воспользовавшись выражением для скорости звука (3.5), можно записать

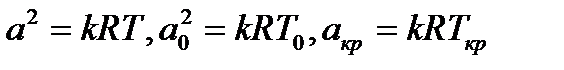
отсюда следует

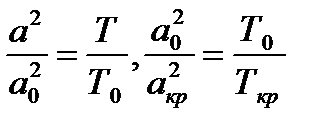
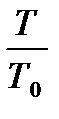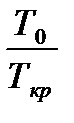Если теперь подставить эти выражения в (7.3) я произвести замену и по формулам (3.8) и (3.9), тогда окончательно получим

(7.4)

Равенство (7.4) можно решать относительно 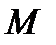, полу­чив тем самым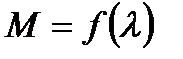

(7.5)

Аналогичные преобразования можно провести и с выражением (7.2) для отыскания зависимости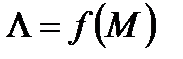

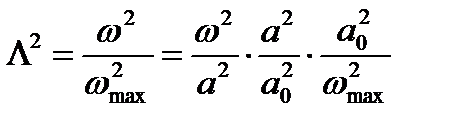(7.6)

где для 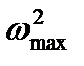необходимо использовать выражение (2.31). После соответствующих преобразований выражения (7.6) получим

(7.7)

При решении газодинамических задач можно пользоваться любым критерием подобия из вышерассмотренных 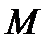, , 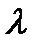. В ряде случаев удобно пользоваться не числом Маха, а коэффициентом скорости 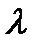и безразмерной скорости . Это хо­рошо видно из таблицы 7.1, где представлены пределы измене­ния указанных критериев подобия.

Таблица 7.1

Критическое и предельные значения критериев подобия

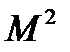
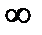
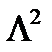
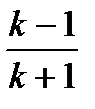
Для облегчения инженерных расчетов газовых потоков вводят понятия газодинамических функций коэффициента скоро­сти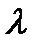

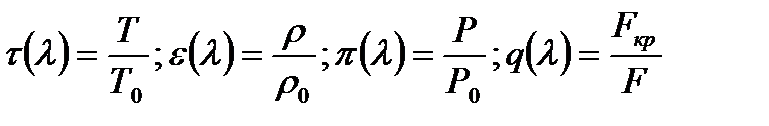(7.8)

Используя ранее полученные выражение (3.8) - для 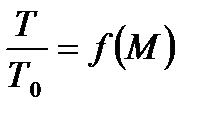, (3.13) для , (3.14) для и (6.7) для 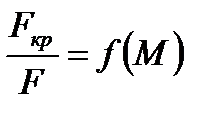и заменяя число через по формуле (7.5), можно получить конкретный вид газодинамических функций

(7.9)

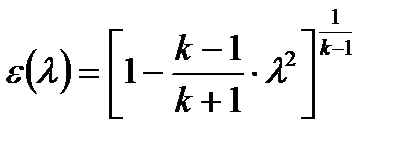(7.10)

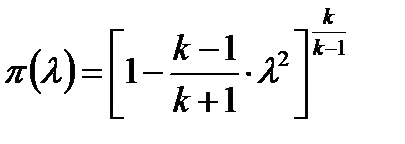(7.11)

(7.12)

Для газодинамических функций составлены таблицы и гра­фики, которые приведены в справочных руководствах для раз­личных значений . В качестве примера на рис. 7.1 пред­ставлен график газодинамических функций для (ме­тан, водяной пар). Таблицы этих функций для двух значений 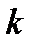приведены в приложении 1.

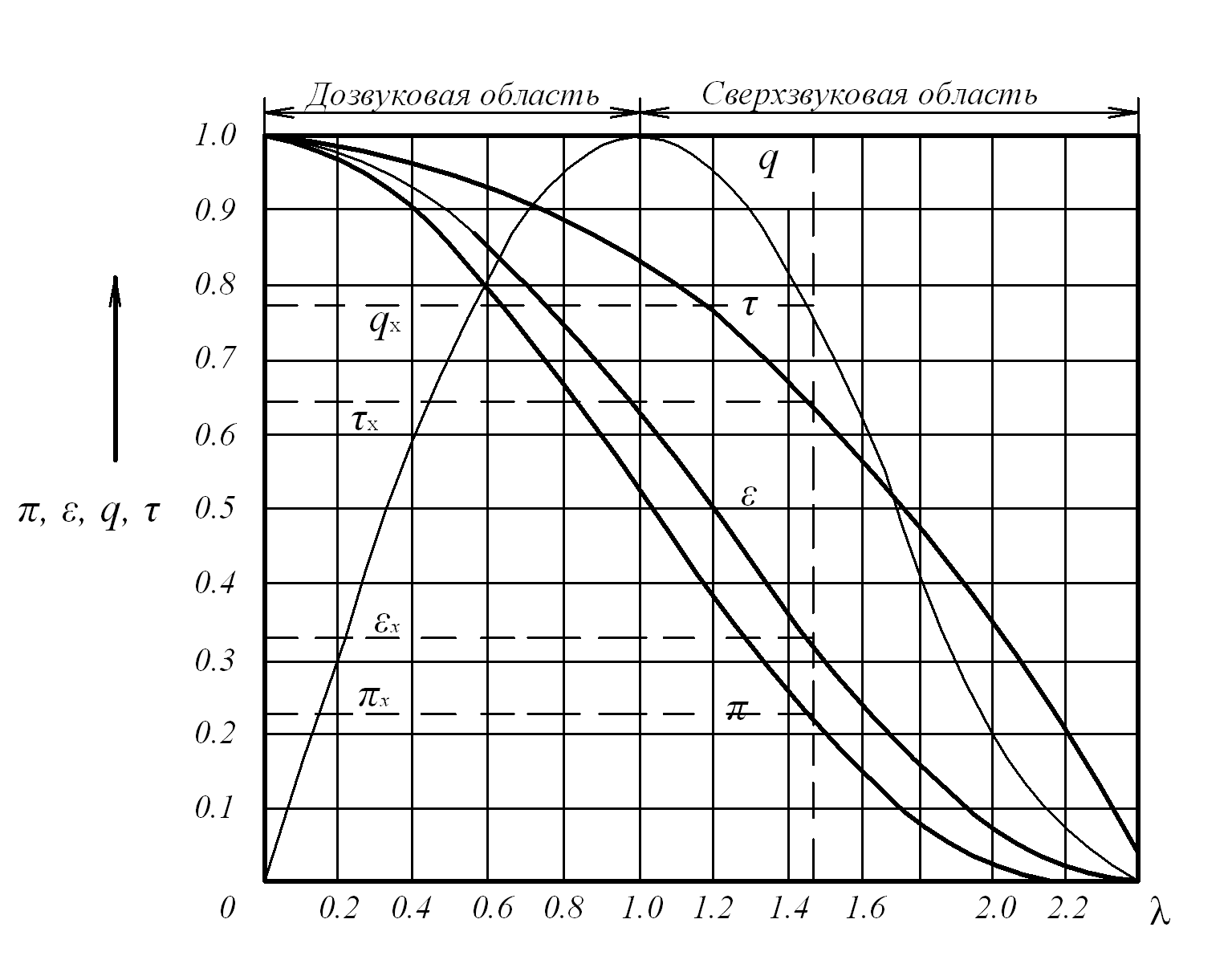
Рис. 7.1 График газодинамических фикций при

Графики и таблицы газодинамических функций позволяют по заданному значению одной из них (например ) быстро находить все остальные.

Между газодинамическими функциями существуют зависимо­сти, которые легко получить, используя выражения (7.8) - (7.11)

(7.12)

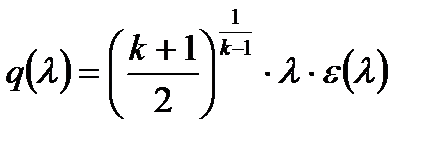(7.13)

Пользуясь газодинамическими функциями, можно предста­вить массовый расход газа в виде

(7.14)

которое с учетом формул (1.3) и (3.10) можно записать иначе

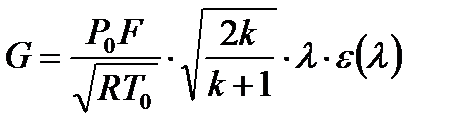(7.15)

Используя зависимость (7.13), выражение примет вид

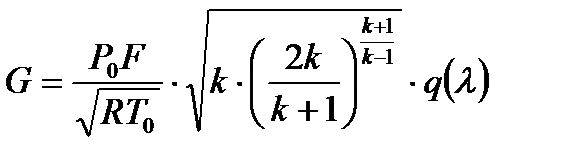(7.16)

Следует заметить, что в формулах (7.14), (7.15) и (7.16) значения 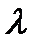и необходимо брать в одном и том же сечении потока газа.

8. СКАЧКИ УПЛОТНЕНИЯ

Date: 2015-08-15; view: 3563; Нарушение авторских прав