
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Косой скачок уплотнения
|
|
Характерной особенностью прямого скачка является то, что, пересекая его фронт, газовый поток не меняет своего направления.
Скачок, фронт которого расположен наклонно к направлению потока, называется косым. Такой скачок получается в случае обтеканий сверхзвуковым потоком профилированных тел. При нерасчетном режиме истечения из сопла Лаваля внутри него иногда образуется сложная система косых скачков уплотнения. При прохождении косого скачка уплотнения газовый поток меняет свое направление. Для установления закономерностей рассмотрим сверхзвуковое обтекание клина (рис. 8.4). С острия клина сходят два плоских  косых скачка уплотнения OA, образующих со скоростью
косых скачка уплотнения OA, образующих со скоростью 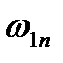 угол
угол 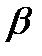
Рис. 8.4. К выводу основных расчетных соотношений для косого скачка уплотнения
Массовый расход газа через единицу площади поверхности фронта OA определяется нормальной составляющей скорости
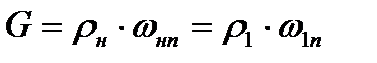 (8.27)
(8.27)
Закон изменения количества движения в векторной форме запишется в виде
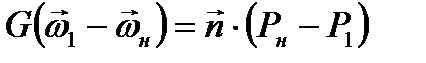 (8.28)
(8.28)
где 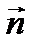 - единичный вектор нормали к поверхности скачка.
- единичный вектор нормали к поверхности скачка.
Проекция уравнения (8.28) на плоскость OA дает соотношение
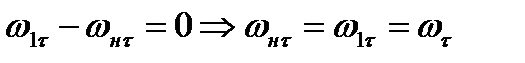 (8.29)
(8.29)
которое позволяет сделать важный вывод: при пересечении скачка уплотнения касательная составляющая скорости не терпит разрыва.
Уравнение (8.28) в проекции на направление 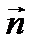 имеет вид
имеет вид
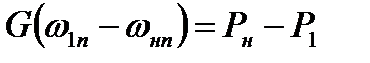 (8.30)
(8.30)
из которого следует, что нормальная составляющая скорости потока терпит разрыв (т.к. 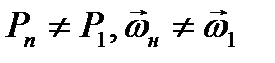 , в противном случае скачка нет).
, в противном случае скачка нет).
Так же как и в случае прямого скачка воспользуемся уравнением энергии в форме (8.11). Подставляя в него выражение энтальпии по формуле (8.12) и значения скоростей
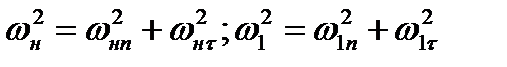
получим, с учетом соотношения (8.29)
 (8.31)
(8.31)
Сравнивая между собой уравнения (8.27), (8.30) и (8.31) для косого скачка с соответствующими уравнениями (8.7), (8.8) и (8.11) для прямого скачка, видим, что указанные системы уравнений совпадают между собой, если в уравнениях для прямого скачка заменить скорости 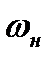 и
и 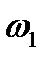 на
на  и
и 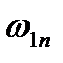 , а величину
, а величину 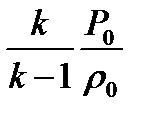 на
на  (8.32)
(8.32)
Следовательно, все формулы, полученные для прямого скачка, остаются в силе, если в них произвести указанную замену. Это равносильно тому, что косой скачок уплотнения сводится к прямому скачку, который сносится вместе с потоком газа по касательной 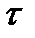 со скоростью
со скоростью  .
.
Адиабата Гюгонио (8.22) полностью сохраняется и для косого скачка уплотнения, т.к. в ней не содержится скорости. Формула Прандтля (8.20) с учетом (8.18) и замены (8.32) для случая косого скачка уплотнения принимает вид
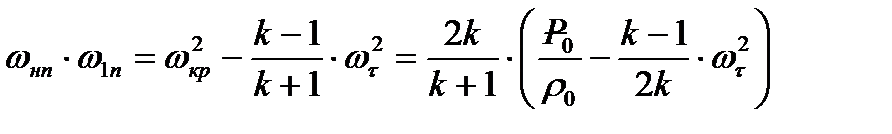 (8.33)
(8.33)
Из формулы (8.33) следует вывод: в случае косого скачка уплотнения всегда  , причем могут реализовываться случаи, когда
, причем могут реализовываться случаи, когда  и
и 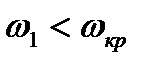 т.к. в отличие от прямого скачка, скорость за косым скачком уплотнения может оставаться сверхзвуковой.
т.к. в отличие от прямого скачка, скорость за косым скачком уплотнения может оставаться сверхзвуковой.
Для косого скачка можно получить соотношение, позволяющее оценить интенсивность изменения давления в зависимости от угла 
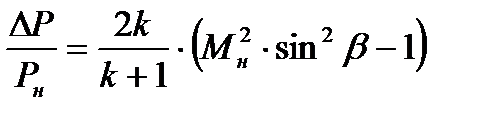 (8.34)
(8.34)
где 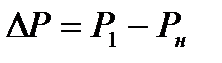
9. ОСНОВНЫЕ ЗАДАЧИ УСТАНОВИВШЕГОСЯ ДВИЖЕНИЯ ГАЗА В ТРУБАХ
Неотъемлемой частью проектирования любого газопровода является газодинамический расчет его линейной части. Этот расчет базируется на закономерностях движения газа в трубах постоянного диаметра, которые и будут рассмотрены ниже. При этом принимается, что движение дозвуковое. Это отвечает реальным условием, т.к. скорость движения газа в линейной части газопровода меньше скорости звука и резко превосходят 50-60 м/с, а числа Маха соответственно значительно меньше единицы. Звуковые скорости могут возникать только в отдельных узлах арматуры (в регуляторах давления и расхода, задвижках и т.п.).
Date: 2015-08-15; view: 3043; Нарушение авторских прав