Закон сохранения массы

Рассмотрим отсек потока газа, ограниченный живыми се­чениями 1-1 и 2-2, отстоящими друг от друга на расстоянии 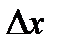(рис. 2.1).

Рис.2.1. К выводу зако­на сохранения массы

Первое сечение характеризуется координатой ( 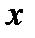- направление вдоль потока), второе – соответственно .

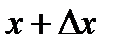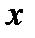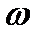Поскольку давление является функцией координаты и газ - сжимаемая среда, то плотность и скорость потока будут также функциями 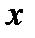. В самом общем случае, когда движение неустановившееся величины 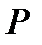, , 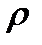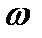являются еще и функциями времени, т.е.

Переменным будет и массовый расход газа 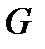. Причем, при неустановившемся течении в любой фиксированный момент времени 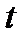массовые расходы газа в первом сечении и во втором сечении 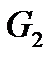определяются

;

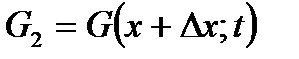(2.1)

Согласно закону сохранения массы, разница и рав­на изменению массы газа, заключенной в отсеке потока дли­ной 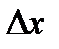. Это изменение должно рассматриваться во времени, масса газа в рассматриваемом отсеке в любой фиксированный момент времени определяется как 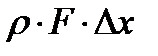. Изменение этой массы во времени определяется как производная по времени .

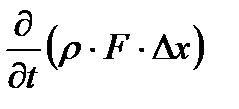Следовательно, согласно закону сохранения массы, мож­но записать

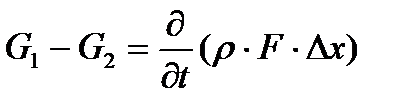(2.2)

Разложим в ряд Тейлора:

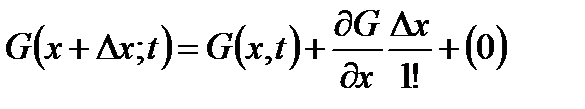
Подставляя это разложение в (2.2) и учитывая, что 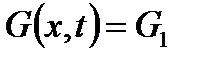, будем иметь:

Поскольку длина отсека 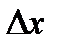не зависит от времени 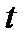, ее можно вынести из под знака производной. После сокращения на 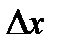последнее равенство можно записать:

Или, если учесть, что массовый расход можно выразить через среднюю скорость потока как произведение ,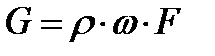

(2.3)

Это уравнение называет уравнением неразрывности (или сплошности) для неустановившегося одномерного течения газа или любой сжимаемой среды.

В случае движения газа в трубах и каналах постоянного сечения 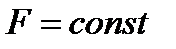уравнение неразрывности (2.3) при­нимает вид

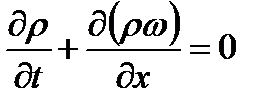(2.4)

В случае установившегося течения газа 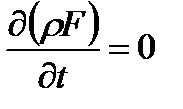и уравнение неразрывности (2.3) принимает вид

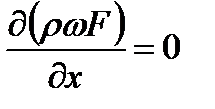
Это равносильно тому, что вдоль потока (при устано­вившемся движении) массовый расход не изменяется

(2.5)

т.е. для любых двух сечений потока газа справедливо равен­ство:

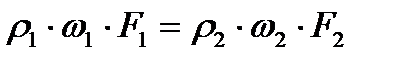(2.5’)

Соотношение (2.5) или (2.5') называют уравнением расхода.

Date: 2015-08-15; view: 610; Нарушение авторских прав