Прямой скачок уплотнения

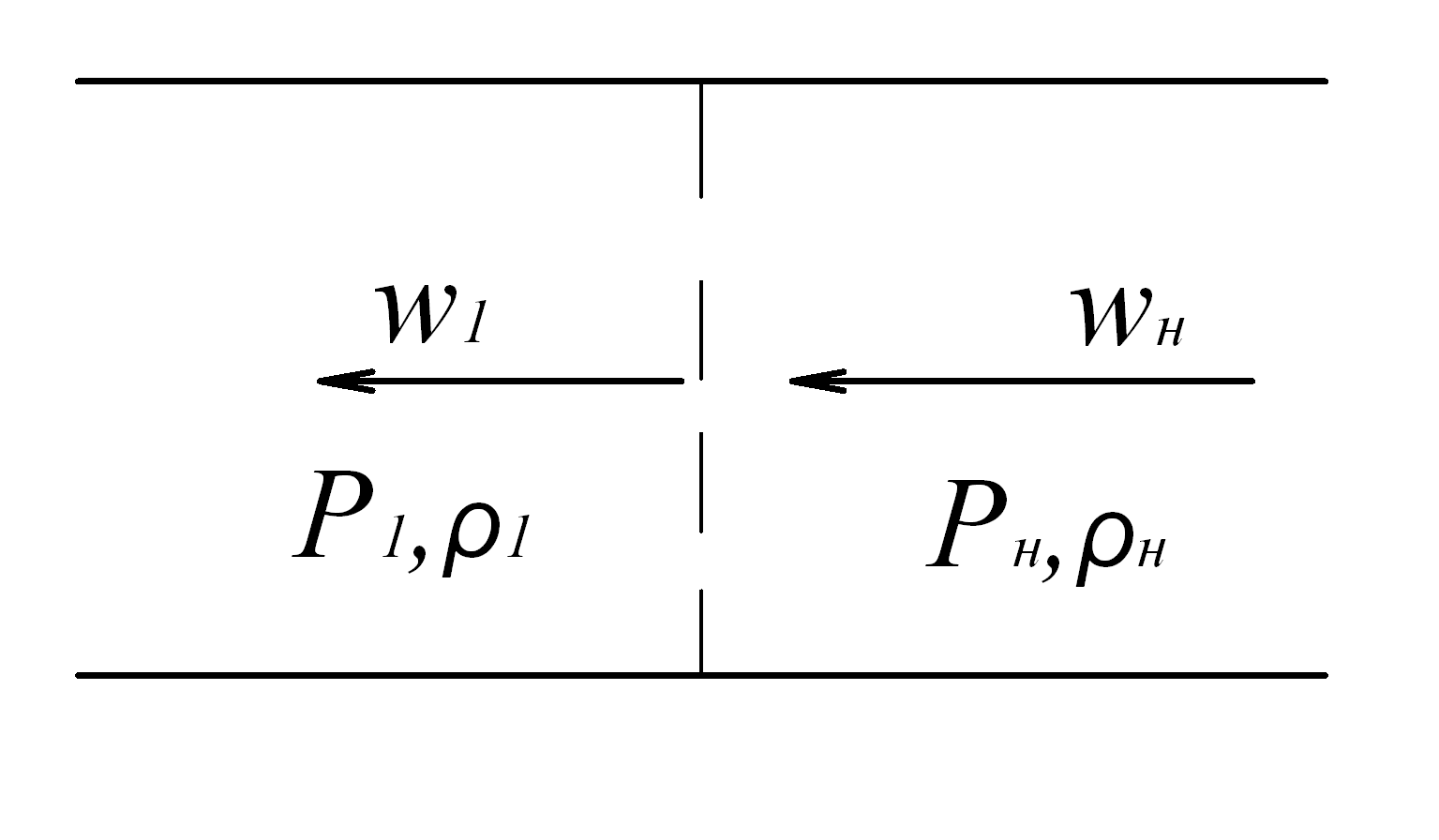Рассмотрим случай, когда фронт сильной волны состав­ляет прямой угол с направлением движения газа. Такая волна называется прямой ударной или прямым скачком уплотнения (рис. 8.2)

Рис. 8.2. Схема прямого скачка уплотнения

Найдем соотношения, связывающие параметры состояния газа перед и за фронтом ударной волны. Рассмотрим схему, когда фронт волны неподвижен. Если же в действительности ударная волна движется, то можно перейти к рассмотрению указанной схемы путем обращения движения. Т.е. остановим фронт волны, направив поток газа навстречу волне со скоро­стью, равной скорости распространения волны 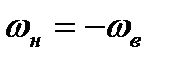. Это равносильно тому, что вводится в рассмотрение система координат, жестко связанная с ударной волной, т.е. система координат движется со скоростью 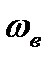. Тогда газ будет пе­ремещаться относительно этой системы координат со скоростью перед фронтом волны и за фронтом волны со скоростью

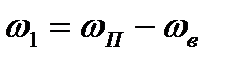(8.6)

Таким образом, в выбранной системе координат имеется неподвижная поверхность (ударная волна), которую пересе­кает газ. При этом параметры потока таза: скорость движения, плотность, давление и температура - претерпевает скачкооб­разное изменение. Именно поэтому ударную волну называют еще скачком уплотнения.

Визуально скачки уплотнения можно наблюдать в сверхзвуковых аэродинамических трубах при обтекании воздухом не­подвижных твердых тел.

Для отыскания связи параметров потока по обе стороны скачка уплотнения воспользуемся уравнением неразрывности, которое для случая 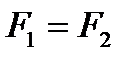принимает вид

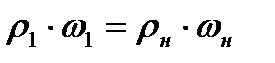(8.7)

и уравнением изменения количества движения

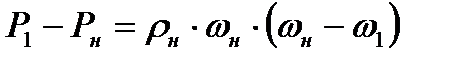(8.8)

Равенство (8.8) можно преобразовать

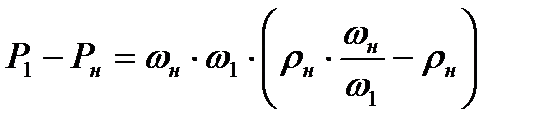
Подставляя сюда выражение 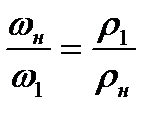, найденное из (8.7), получим

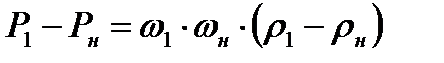(8.9)

или

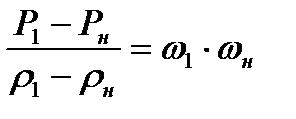(8.10)

Найдем соотношение, связывающее скорость газа по обе стороны скачка уплотнения со скоростью звука. Для этого вос­пользуемся уравнением Бернулли-Сен-Венана для двух сечений, расположенных на бесконечно близком расстоянии друг от дру­га: одно сечение выбрано но одну сторону скачка уплотнения (в невозмущенной области), другое - за скачком уплотнения

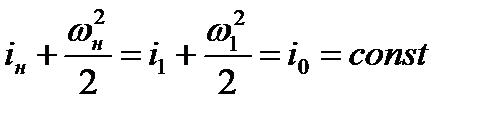(8.11)

Правомерность использования этого уравнения вытекает из того, что боковая поверхность отсека потока 1-Н (т.е. в области скачка) ничтожна мала, энергообменом через эту по­верхность можно пренебречь.

Согласно (1.18) можно записать

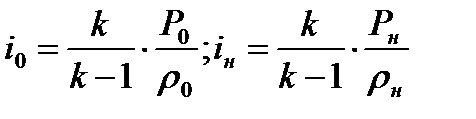(8.12)

Подставляя эти значения энтальпии в (8.11) и решая уравнение относительно 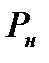, получим

(8.13)

По аналогии из (8.11), с учетом (8.12), можно по­лучить равенство

(8.14)

Вычитая почленно равенство (8.13) из (8.14), имеем

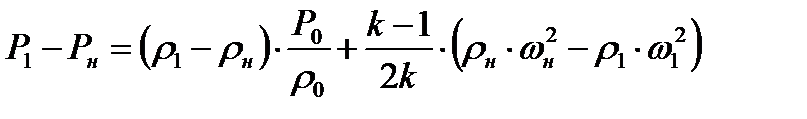(8.15)

Используя соотношение (8.7), преобразуем равенство (8.8) к виду

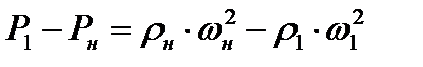(8.16)

Подставляя (8.16) в (8.15), после несложных выкла­док можно получить

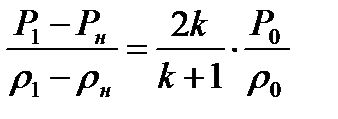(8.17)

Воспользуемся выражением (3.10), которое с учетом уравнения Клапейрона-Менделеева (1.3) примет вид

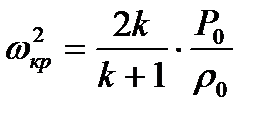(8.18)

Используя последнее равенство, могло выражение (8.17) представить к виду

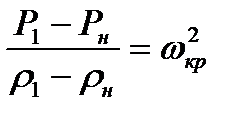(8.19)

Сопоставляя равенства (8.10) и (8.19), можно по­лучить искомое соотношение, связывающее скорости потока га­за перед и за скачком уплотнения с критической скоростью.

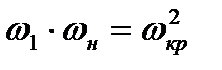(8.20)

Последнее соотношение называется формулой Прандтля. Его можно представить еще иначе, если заменить в нем ско­рост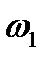и и 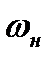через соответствующие значения коэффициента скорост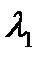и и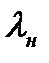

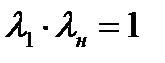(8.21)

Соотношения (8.20) и (8.21) позволяют сделать важ­ный вывод. В прямом скачке уплотнения всегда сверхзвуковая скорость газа переходит в дозвуковую, так как если 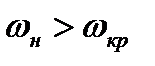, то 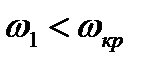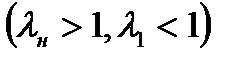. Более того, чем выше значение безразмерной скорости 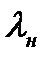(следовательно и 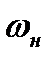), тем меньше ее значение после скачка. Иными словами, чем вы­ше начальная скорость сверхзвукового потока, тем сильнее получается скачок уплотнения. С уменьшением начальной ско­рости скачок ослабевает и исчезает совсем, при 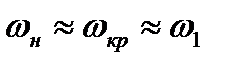Тем самым доказывается, что ударные волны возможны только при сверхзвуковых течениях газа. Этот вывод подтверждается и экспериментально.

Установим теперь связь между давлением и плотностью газа в скачке уплотнения. Для этого используя выражение (8.13) и (8.14) и исключая из них скорост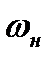и и 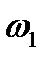, с учетом (8.9) можно получить (выкладки опускаются)

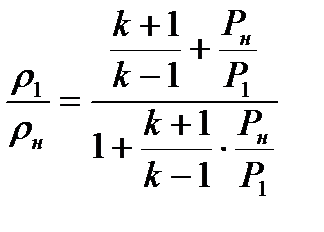(8.22)

Соотношение (8.22) позволяет судить о термодинами­ческом процессе изменения состояния газа в скачке уплотне­ния и называется ударной адиабатой или адиабатой Гюгонио.

Следует подчеркнуть, что при прохождении газа через скачок уплотнения уравнение адиабаты Пуассона (1.21) те­ряет силу, т.е. процесс движения газа становится неизоэн- тропийным. Вместо (1.21) должно использоваться уравнение ударной адиабаты (8.22).

Из (8.22) видно, что при неограниченном возрастании давления в скачке уплотнения 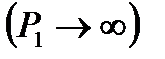увеличение плотно­сти имеет определенный предел

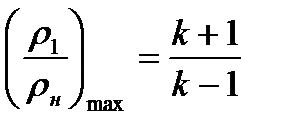(8.23)

Например, для воздуха (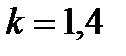) увеличение плотности в скачке уплотнения может быть не более чем в 6 раз (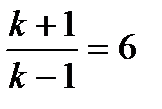). Если бы процесс оставался адиабатическим (при прохождении скачка уплотнения), то увеличение плотно­сти с ростом давления было бы неограниченным. Это следует из выражения

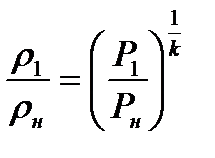(8.24)

которое получается при формальном использовании уравнения (1.21).

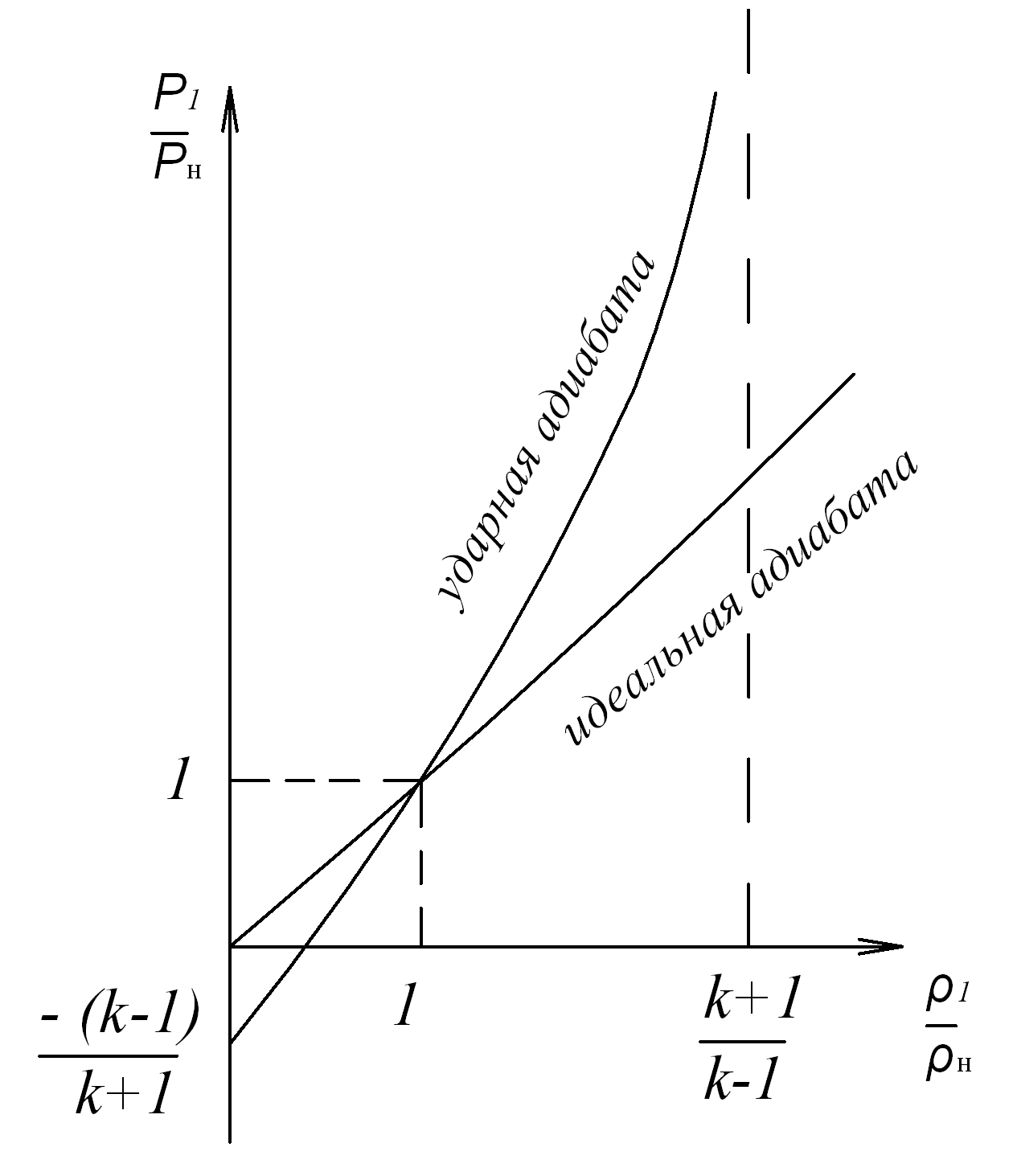Графическое представление зависимостей (8.22) и (8.24) дается на рис. 8.3

Рис. 8.3. Графическое представ­ление ударной (Гюгонио) и идеальной (Пуассона) адиабат

Выражение (8.22) иногда удобнее использовать в другом

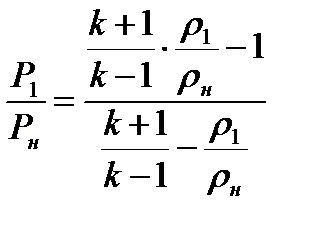(8.25)

Можно выразить отношение давлений в прямом скачке уп­лотнения и в функции коэффициента скорости перед скачком уплотнения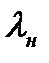

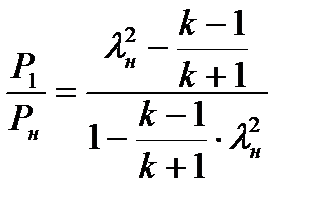(8.26)

которое получается из (8.25) исключением плотности.

Выражения (8.25) и (8.26) позволяют определять потери полного давления в прямом скачке уплотнения.

Date: 2015-08-15; view: 2666; Нарушение авторских прав