Центрированная оптическая система и ее кардинальные элементы

Идеальной оптической называют систему, в которой сохраняется гомоцентричность пучков и изображение оказывается строго геометрически подобно предмету. Каждой точке пространства объектов соответствует в идеальной системе точка пространства изображений. Эти точки носят название сопряженных точек. Точно также каждой прямой или плоскости пространства объектов должна соответствовать сопряженная прямая или плоскость пространства изображений.

Изложенное раньше показывает, что идеальная оптическая система может быть осуществлена в виде центрированной оптической системы, если ограничиться параксиальными лучами. Как показывает теория, изображение предметов с помощью идеальной оптической системы может быть построено без детального исследования хода лучей внутри системы и требует только знания ряда так называемых кардинальных точек и плоскостей, задание которых полностью описывает все свойства оптической системы.

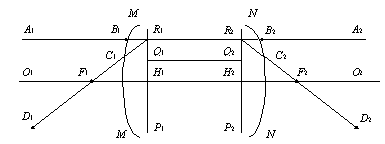
Р и с. 7.9

Линия, соединяющая центры сферических поверхностей, представляет собой ось симметрии центрированной системы и называется главной оптической осью системы.

Пусть MM и NN – крайние поверхности, ограничивающие оптическую систему, а О ₁ О ₂ – главная оптическая ось (рис. 7.9). Проведем луч А ₁ В ₁ параллельный главной оптической оси. Этому лучу соответствует луч C ₂ D ₂, выходящий из системы. Ход луча внутри оптической системы нас интересовать не будет. Точка F ₂ пересечения луча C ₂ D ₂ с главной оптической осью является изображением бесконечно удаленной точки (это легко показать с помощью второго луча, распространяющегося вдоль главной оптической оси). Точку F ₂ называют задним фокусом системы (фокусом в пространстве изображений). Плоскость, перпендикулярная к О ₁ О ₂ и проходящая через F ₂, называется фокальной плоскостью. Задний фокус оптической системы не всегда, конечно, лежит справа от нее, как это изображено на рис. 7.9. Так, в рассеивающих системах этот фокус может лежать и слева от всех поверхностей, входящих в состав системы.

Рассмотрим теперь луч А ₂ В ₂, входящий в систему справа и лежащий на продолжении луча А ₁ В ₁. Слева из системы выйдет луч C ₁ D ₁, сопряженный лучу А ₂ В ₂. Точку F ₁ называют передним фокусом системы (фокусом в пространстве предметов). Исходящие из него лучи в пространстве изображений параллельны оптической оси. Продолжим теперь C ₁ D ₁ и C ₂ D ₂ до пересечения с продолжениями А ₁ В ₁ и А ₂ В ₂ и отметим точки пересечения R ₁ и R ₂. Легко видеть, что эти точки сопряжены, т.е. являются изображением друг друга. Действительно, точка R ₁ лежит на пересечении лучей А ₁ В ₁ и С ₁ D ₁, а точка R ₂ – на пересечении сопряженных лучей А ₂ В ₂ и С ₂ D ₂ (для большей наглядности направление одной пары сопряженных лучей, например, А ₂ В ₂ и С ₁ D ₁, можно изменить на противоположное, пользуясь обратимостью световых лучей). Из построения ясно, что точки R ₁ и R ₂ лежат на одинаковом расстоянии от главной оптической оси, т.е. R ₁ H ₁ = R ₂ H ₂ (линейное поперечное увеличение равно 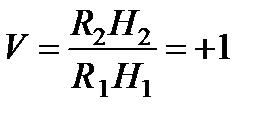). Можно показать, что в идеальной системе все точки плоскости P ₁, перпендикулярной к главной оптической оси и проходящей через R ₁, попарно сопряжены точкам плоскости P ₂, также перпендикулярной к главной оптической оси и проходящей через R ₂. При этом сопряженные точки находятся на одинаковых расстояниях от оси (например, точки Q ₁ и Q ₂ на рис. 7.9).

Две сопряженные плоскости Р ₁ и Р ₂, отражающие друг друга с поперечным увеличением V = + 1, называются главными плоскостями, а точки H ₁ и H ₂ – главными точками системы. Расстояния от главных точек до фокусов называются фокусными расстояниями: f ₁ = H ₁ F ₁; f ₂ = H ₂ F ₂. В том случае, когда с обеих сторон системы находится одна и та же среда (например, воздух) .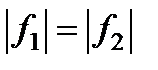

Если известно положение фокусов и главных плоскостей, изображение предмета может быть найдено путем простых геометрических построений с использованием двух лучей, исходящих из одной точки. Рис. 7.10 иллюстрирует эти построения. Луч 1, проведенный параллельно главной оси, имеет в качестве сопряженного луч 1¢, пересекающий вторую главную плоскость на высоте H ₂ D ₂ = H ₁ D ₁ и проходящий через фокус F ₂. Луч 2, проходящий через фокус F ₁ и пересекающий главную плоскость на высоте Н ₁ С ₁, пройдет на той же высоте (Н ₁ С ₁ = Н ₂ С ₂) через вторую главную плоскость и пойдет параллельно главной оси.

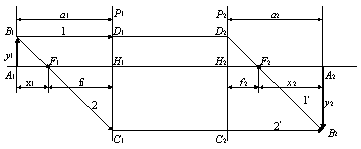
Р и с. 7.10

Оптическая система называется положительной (собирающей), если передний фокус F ₁, лежит левее главной плоскости Р ₁, а задний фокус F ₂ – правее главной плоскости Р ₂. Если же F ₁ располагается правее Р ₁, а F ₂ – левее Р ₂, система называется отрицательной или рассеивающей. Фокусному расстоянию систем приписывается определенный знак: плюс – для собирающих систем и минус – для рассеивающих. Если определить положение предмета и изображения по их расстояниям от соответствующих главных плоскостей, то легко установить соотношение между этими расстояниями (а ₁ и а ₂) и фокусным расстоянием системы, которое аналогично формуле.

Положение предмета и его изображения можно определять относительно фокусов F ₁ и F ₂ (рис. 7.10). Обозначая эти расстояния соответственно через x ₁ и x ₂ и рассматривая две пары подобных треугольников А ₁ В ₁ F ₁ F ₁ H ₁ С ₁ и H ₂ D ₂ F ₂ F ₂ A ₂ B ₂, по определению линейного увеличения запишем

, .

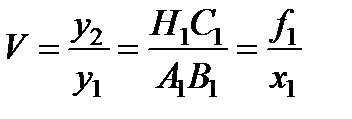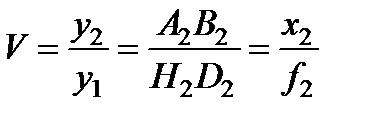Отсюда следует, что f ₁/ x ₁ = x ₂/ f ₂ или 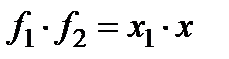. Из рис. 7.10 видно также, что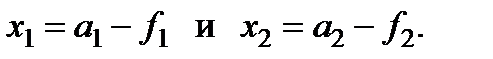

С учетом последних соотношений формула примет вид: .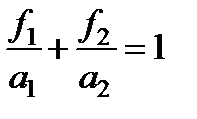

Соотношения,, наряду с, определяющие положение сопряженных точек в данной системе, играют роль формул системы.

Пользуясь правилом знаков, можно описать все свойства как собирательных, так и рассеивающих систем.

Следует подчеркнуть, что главные плоскости и главные точки могут лежать как внутри, так и вне системы и при этом могут располагаться как угодно несимметрично относительно поверхностей, ограничивающих оптическую систему.

Большой практический интерес представляет случай, когда размер системы в направлении главной оптической оси значительно меньше фокусного расстояния. В этом случае оптический луч, проходя внутри системы, мало смещается, так что точки С ₁ и В ₁, С ₂ и В ₂ (рис. 7.9) практически совпадают. Главные плоскости (и главные точки Н ₁, Н ₂) при этом совмещаются друг с другом и располагаются посредине системы. Такая оптическая система называется тонкой линзой. Расстояния а ₁ и а ₂ и фокусные расстояния можно в этом случае приближенно отсчитывать от центра линзы.

Кроме линейного увеличения, систему можно характеризовать угловым увеличением W, понимая под W отношение тангенсов углов u ₂ и u _1, составляемых сопряженными лучами А ₂ M ₂ и A ₁ M ₁ с оптической осью (рис. 7.11), т.е. W = tg u ₂/tg u ₁

Из рис. 7.11 видно, что W = a ₁/ a ₂ (ибо H ₁ M ₁ = H ₂ M ₂), тогда как линейное увеличение V = n ₁ a ₂/ n ₂ a ₁, т.е.

.

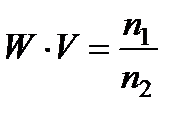Если предмет и изображение расположены в одной среде (n ₁ = n ₂), то W × V = 1.

Как угловое, так и линейное увеличение системы различно для разных точек оси, причем чем больше линейное увеличение, тем меньше угловое.

Сопряженные точки, в которых угловое увеличение системы W = 1, представляют собой особенные точки системы. Эти точки называются узлами (или узловыми точками) и характеризуются тем, что сопряженные лучи, проходящие через узлы, параллельны друг другу, ибо u ₁ = u ₂.

В каждой системе такой парой точек будут точки N ₁ и N ₂, отстоящие от первого и второго фокусов соответственно на расстояния равные x ₁ = F ₁× N ₁ = f ₂ и x ₂ = F ₂× N ₂ = f ₁. Координаты этих точек удовлетворяют уравнению системы, т.е. они являются сопряженными.

Их расстояния относительно главных плоскостей равны соответственно H ₁ N ₁ = a ₁¢ = f ₁ – f ₂ и H ₂ N ₂ = a ₂¢ = f ₁ – f ₂, следовательно, для этих точек угловое увеличение равно 1, т.е. они служат узловыми точками системы.

Плоскости, проходящие через узлы перпендикулярно к оптической оси, называются узловыми плоскостями. Шесть плоскостей (две фокальные, две главные и две узловые) и шесть точек главной оси, им соответствующие (фокусы, главные точки, узлы), называются кардинальными плоскостями и точками.

Зная свойства кардинальных плоскостей и точек, можно построить изображение предмета в любой системе. На рис. 7.10 показано, как можно построить изображение, если дано расположение ее главных плоскостей и фокусов. На рис. 7.11 используется еще один луч (луч 3), идущий через узел N ₁. Ему сопряженный луч 3¢ проходит через узел N ₂ и параллелен лучу 3. Для построения изображения предмета можно ограничиться двумя лучами из трех.

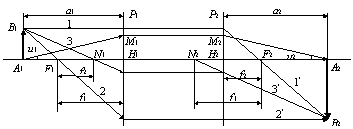
Р и с. 7.11

Когда по обе стороны системы располагается одна и та же среда, то фокусные расстояния f ₁ и f ₂ равны по абсолютной величине. Узловые точки в этом случае сливаются с главными.

Тонкая линза может рассматриваться как частный случай толстой линзы, в которой точки Н ₁ и Н ₂ совпадают, и главные плоскости сливаются. Узловые точки, совмещенные с Н ₁ и Н ₂, также совпадут, образуя оптический центр линзы.

Date: 2015-08-06; view: 660; Нарушение авторских прав