Изображение малых предметов. Увеличение

Выберем в качестве предмета линию А ₁ В ₁, перпендикулярную к оптической оси, и построим ее изображение А ₂ В ₂ (рис. 7.7) Р и с. 7.7

Для графического отыскания точки В ₂ можно провести луч В ₁ В ₁ ║ А ₁ О, тогда преломленный луч должен пройти через фокус F ₂. Луч В ₁ С, проходящий через центр С сферической поверхности, не изменяет направления своего распространения.

Отношение линейных размеров изображения (y ₂ = A ₂ B ₂) и предмета (y ₁ = A ₁ B ₁) носит название линейного или поперечного увеличения V: 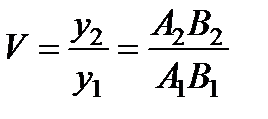. Из треугольников А ₁ В ₁ О и А ₂ В ₂ О имеем 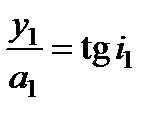, 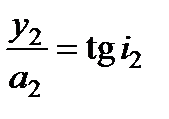где а ₁ и а ₂ – расстояния от преломляющей поверхности до предмета и до его изображения, соответственно.

При малых размерах А ₁ В ₁ и А ₂ В ₂ (параксиальное приближение) 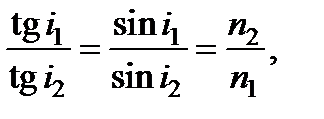так что 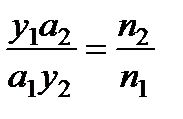или .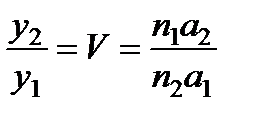

Для преломляющей системы n ₁ и n ₂ всегда положительно и поэтому знак V определяется знаком отношения а ₂/ а ₁. Для расположений, соответствующих действительному изображению, как на рис. 7.7, а ₁ и а ₂ имеют разные знаки, т.е. V – отрицательно и изображение перевернутое; для мнимых изображений – наоборот.

Плоскость предмета A ₁ B ₁ и плоскость его изображения A ₂ B ₂ являются сопряженными по отношению к данной оптической системе. Сопряженные плоскости называются главными, если для них V = 1, т.е. изображение получается прямым и в натуральную величину.

Из формул и следует, что для сферической поверхности главные плоскости совпадают между собой и представлены плоскостью, касательной к сфере в точке 0, т.е. а ₁ = а ₂ = 0. Поэтому фокусные расстояния сферической поверхности следует считать расстояниями от главных плоскостей до фокусов.

На рис. 7.7 изображены также углы u ₁ и u ₂, определяющие максимальное раскрытие (апертуру) пучков, падающих на сферическую поверхность (угол 2 u ₁), и сопряженных им изображающих пучков (угол 2 u ₂). Предельное значение этих углов определяется требованием соблюдения условий параксиальности, когда изображение небольшого предмета будет передаваться без искажения.

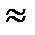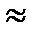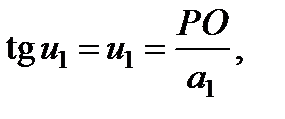
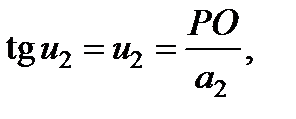
Для параксиальных лучей A ₁ P A ₁ O = a ₁ и PA ₂ OA ₂ = a ₂, поэтому 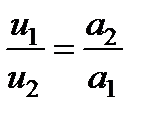, и на основании имеем 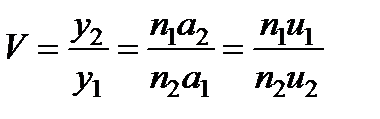или ..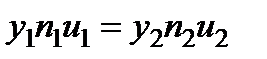

Соотношение носит название теоремы Лагранжа-Гельмгольца и справедливо для параксиальных лучей.

Получение четких изображений при употреблении пучков со значительной апертурой возможно лишь при выполнении условия синусов Аббе: .

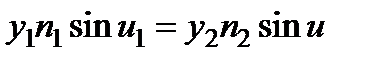Строение пучка, преобразованного оптической системой, может быть только таким, какое допускают условия или.

Date: 2015-08-06; view: 413; Нарушение авторских прав