Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Преломление на сферической поверхности
|
|
Рассмотрим простейший случай преломления света на одной сферической поверхности, разграничивающей однородные среды с показателями преломления n 1 и n 2. Пусть эта поверхность обладает симметрией вращения относительно одной из прямых OC, проходящей через центр кривизны сферической поверхности, которую будем называть главной оптической осью (рис. 7.6).
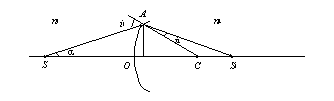
Р и с. 7.6
В дальнейшем все отрезки вдоль оси будем отсчитывать от точки O, считая их положительными, если они откладываются от точки O вправо, т.е. в направлении распространения света, и отрицательными – если они откладываются влево.
Допустим, что точечный источник света S находится на оптической оси системы. Произвольный луч SA, падающий на сферическую поверхность под углом i 1, после преломления на поверхности под углом i 2 пройдет по пути AS 1. Обозначим длины AS и AS 1 через a 1 и а 2, соответственно.
Распишем площади полученных треугольников. Из рис. 7.6 видно, что
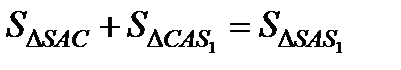. Учитывая, что a 1 < 0, a 2 > 0 можно записать: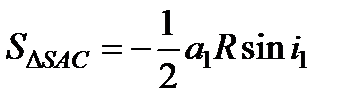 
, 
,
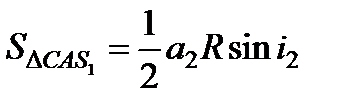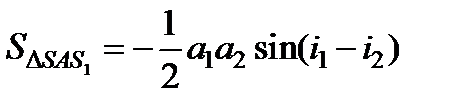где AC = R – радиус кривизны преломляющей поверхности. Он отсчитывается от сферической поверхности к ее центру и положителен в нашем случае. Подставляя выражения,, в формулу, получим:
.
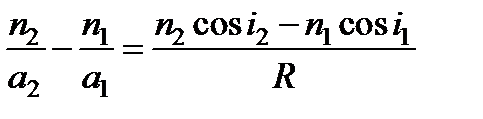Согласно формуле, положение точки S 1 зависит от угла наклона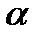 
падающего луча к оптической оси, т.е. от угла падения i 1 и преломления i 2. Ограничимся малыми углами 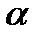, i 1, i 2. Лучи, удовлетворяющие такому условию, называются параксиальными (приосевыми). Для них можно записать 
; 
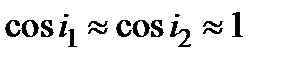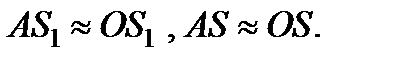В этом приближении формула принимает вид: 
.
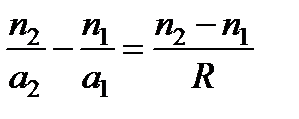В случае параксиального приближения положение точки S 1 не зависит от угла a. Следовательно, все параксиальные лучи, выходящие из одной точки оптической оси, после преломления на сферической поверхности пересекутся в одной точке, лежащей также на оптической оси. Точка S 1 будет поэтому оптическим изображением точки S в параксиальных лучах, а расстояния а 1 и а 2 будут обозначать соответственно расстояния от сферической поверхности до предмета и до изображения.
Формуле можно придать вид: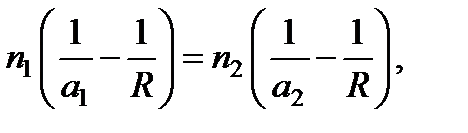 
откуда следует, что произведение n (1/ a – 1/ R) при преломлении сохраняет свою величину. Его называют нулевым инвариантом Аббе.
Основное уравнение охватывает все случаи преломления лучей на сферической поверхности. Пользуясь установленным выше правилом знаков, можно разобрать случай выпуклой (R > 0) или вогнутой поверхности (R < 0). Точно также, в зависимости от того, будут ли а 1 и а 2 иметь разные знаки или одинаковые, мы будем иметь случаи, когда изображение располагается с противоположной по сравнению с источником стороны преломляющей поверхности или лежит по одну сторону с ним. В первом случае (а 2 > 0) точка, именуемая изображением, есть действительно точка пересечения преломленных лучей. Такое изображение называется действительным. Во втором случае (а 2 < 0), преломленные лучи, идущие во второй среде, остаются расходящимися и реально не пересекаются. Название изображения относится к той воображаемой точке, которая представляет собой место пересечения предполагаемого продолжения преломленных лучей. Такое изображение называется мнимым.
Date: 2015-08-06; view: 588; Нарушение авторских прав