Геометрическая оптика как предельный случай волновой оптики

Рассмотрим переход от волновой оптики к геометрической в предельном случае исчезающе малой длины волны (l ® 0).

Плоская волна характеризуется тем свойством, что ее поверхности постоянной фазы (волновые поверхности) представляют собой неограниченные плоскости, а направление ее распространения и амплитуда везде одинаковы. В общем случае световые волны таким свойством не обладают. Тем не менее часто световую волну можно приближенно рассматривать как плоскую в каждом небольшом участке пространства. Это возможно тогда, когда амплитуда световых колебаний и направление распространения волны почти не изменяются на расстоянии порядка длины волны. Волновые поверхности при этом имеют небольшую кривизну и на небольших участках пространства можно, как и у плоской волны, говорить об определенном направлении распространения, нормальном к волновой поверхности. Для характеристики этого направления вводят понятие лучей, т. е. линий, касательная к которым в каждой точке совпадает с направлением распространения волны.

Геометрическая оптика, отвлекаясь от волновой природы света, описывает его распространение с помощью лучей. При этом оказывается, что поведение лучей при l ® 0 определяется теми же законами, что и для плоских волн: законы преломления и отражения, установленные для плоской волны, падающей на плоскую границу раздела, справедливы в приближении геометрической оптики при более общих условиях. Например, при падении луча на поверхность линзы направление, интенсивность и состояние поляризации отраженного и преломленного лучей можно найти из соответствующих формул для плоских волн.

В плоской монохроматической волне, распространяющейся в изотропной однородной среде с показателем преломления n, зависимость напряженности поля от координат и времени имеет вид

.

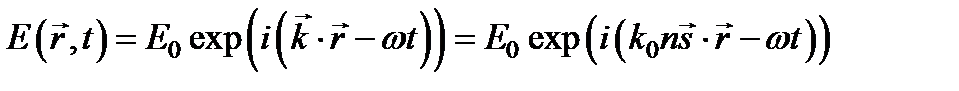Здесь введен единичный вектор 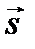(лучевой вектор), указывающий направление распространения плоской волны: 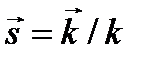. Поэтому ,

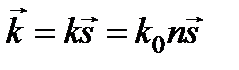где 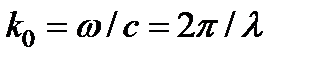— волновое число (для вакуума). В неоднородной среде показатель преломления зависит от координат: 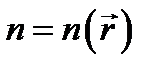— и выражение уже не будет решением уравнений Максвелла. Можно искать решение в виде монохроматической волны более общего типа:

,

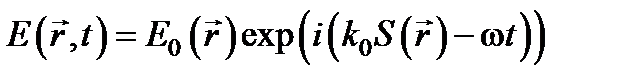где величина 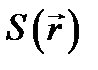, называемая эйконалом, представляет собой вещественную скалярную функцию координат, а амплитуда 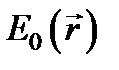зависит от положения рассматриваемой точки. Выражение будет давать приближенное решение уравнений Максвелла в предельном случае больших k ₀ (т. е. малых длин волн l ₀) при условии, что функция 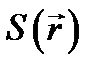удовлетворяет некоторому дифференциальному уравнению (уравнению эйконала). Найдем его.

Напряженность поля 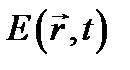в при l ® 0, т.е. k ₀ ® ¥, испытывает очень быстрые изменения в пространстве, но амплитуда 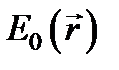и эйконал 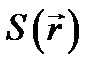изменяются постепенно и при k ₀ ® ¥ остаются конечными. В малых участках пространства 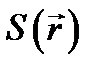можно разложить в ряд, ограничившись членами первого порядка: .

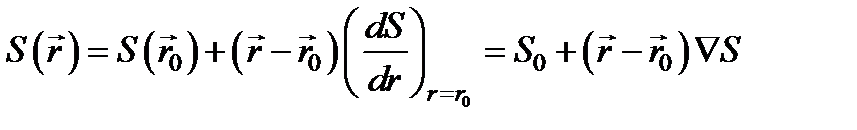Подставляя это разложение в, представим напряженность поля в окрестности точки 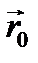в виде

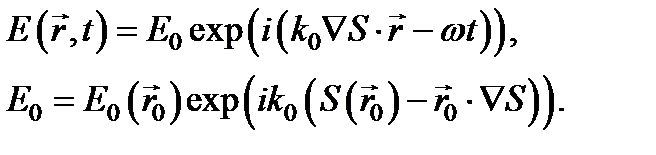
Это и значит, что в каждом малом участке пространства, в пределах которого справедливо разложение, произвольную волну можно рассматривать как плоскую, так как в зависимость напряженности от координат 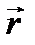такая же, как и в плоской волне. Сравнивая с, получаем дифференциальное уравнение, которому должна удовлетворять функция 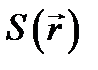: 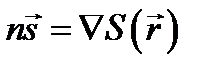или 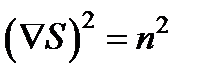. Поверхности равных фаз (волновые поверхности) монохроматической волны определяются уравнением .

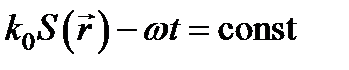Уравнение показывает, что лучи, т. е. линии, касательные к которым в каждой точке совпадают с направлением распространения волны, задаваемым единичным вектором 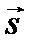, ортогональны к волновым поверхностям. В общем случае при показателе преломления 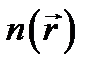, изменяющемся от точки к точке, лучи будут искривлены. Поверхности равных фаз перемещаются в направлении луча 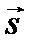со скоростью 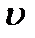= c / n.

Чтобы выяснить, как искривляются лучи в оптически неоднородной среде, получим из уравнения эйконала дифференциальное уравнение для лучей. Радиус-вектор 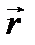точки P, лежащей на луче, будем рассматривать как функцию длины дуги. Тогда 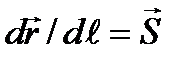и из находим 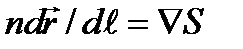. Продифференцируем это уравнение по 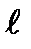и преобразуем правую часть следующим образом: d / d 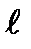(Ñ S) = Ñ(dS / d 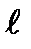) = Ñ n (здесь мы воспользовались тем, что dS / d 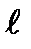= 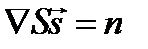Ñ S = n). Таким образом,

.

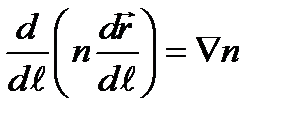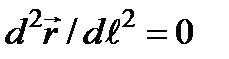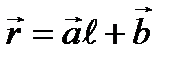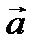В частности, в однородной среде n = const, Ñ n = 0 и принимает вид . Его решение , где и 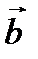– постоянные векторы, представляет собой прямую линию, направленную по вектору 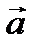и проходящую через точку 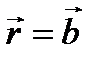. В однородной среде световые лучи прямолинейны. Но волновые поверхности 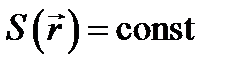при этом могут и не быть плоскими. Например, одно из возможных решений уравнения эйконала (Ñ S)² = n ² при n = const имеет вид:

(особая точка при 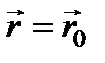). В этом случае 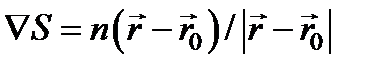и лучи света образуют семейство прямых, расходящихся из точки 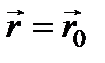, а волновые поверхности – концентрические сферы.

Для неоднородной среды 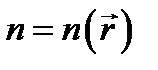и уравнение преобразуется к виду .

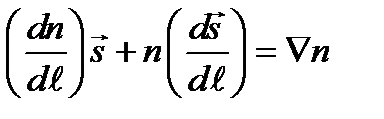Так как 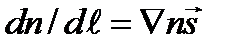, то .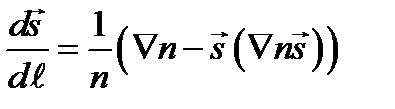

Производная единичного вектора 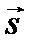по длине луча 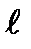характеризует кривизну луча: 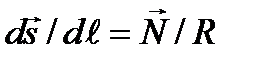, где – единичный вектор главной нормали к лучу, R – радиус его кривизны. Умножая обе части скалярно на 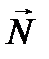и учитывая, что 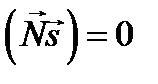, получаем следующее выражение для радиуса кривизны луча: .

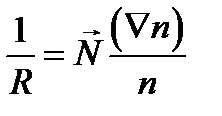Отсюда, в частности, следует, что 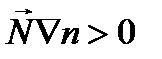, т.е. угол между 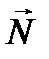и Ñ n острый — луч изгибается в область с большим показателем преломления n.

Для демонстрации искривления световых лучей можно взять две смешивающиеся жидкости, например сероуглерод (n = 1,63) и бензол (n = 1,50), и расположить их слои один над другим. Граница между слоями вскоре пропадает вследствие диффузии, и получается среда с непрерывно изменяющимся показателем преломления. Исходя из уравнения, можно показать, что в среде, показатель преломления которой изменяется в каком-либо одном направлении по линейному закону n (z) = n ₀(1 + az), лучи представляют собой цепные линии (рис. 7.1а). Если начало координат выбрать там, где вектор 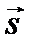направлен горизонтально (вдоль оси х), уравнение луча имеет вид .

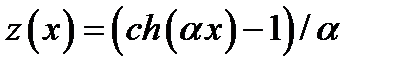В соответствии с луч сильнее всего искривлен там,

Р и с. 7.1

где его направление перпендикулярно градиенту показателя преломления.

Искривлением лучей света в неравномерно нагретом воздухе объясняется явление миража, когда в жаркой пустыне возникает иллюзия находящейся на горизонте водной глади или вдали на асфальте нагретого солнечными лучами шоссе видны «лужи», исчезающие при приближении к ним. Прилегающие к раскаленной земле слои воздуха нагреты сильнее, поэтому плотность воздуха и его показатель преломления возрастают с высотой. Лучи света, входящие в такой слой под небольшими углами, искривляются и, не достигнув земли, выходят обратно под такими же углами. Мы настолько привыкли к прямолинейному распространению света, что подсознательно считаем источник расположенным на прямолинейном продолжении попадающих в глаз лучей даже тогда, когда они искривлены; мы видим расположенные над горизонтом удаленные предметы как бы отраженными горизонтальной зеркальной поверхностью («водной гладью»).

Другой пример искривления лучей дает явление астрономической рефракции, обусловленное тем, что плотность земной атмосферы и, следовательно, ее показатель преломления убывают с высотой. Наблюдаемая высота небесного светила над горизонтом оказывается больше истинной. Эффект особенно значителен, когда светило наблюдается у горизонта (рефракция при этом достигает 35') и быстро убывает с увеличением высоты. Этим объясняется сплюснутая форма солнечного диска при восходе и закате. Благодаря рефракции мы видим Солнце в течение нескольких минут после того, как оно уже зашло.

Выше предполагалось, что показатель преломления представляет собой непрерывную функцию координат. Чтобы рассмотреть поведение лучей при переходе через резкую границу раздела сред с различными показателями преломления, можно мысленно заменить граничную поверхность тонким переходным слоем, в котором показатель преломления изменяется непрерывно. Тогда уравнение останется в силе. Применяя к обеим его частям операцию rot и учитывая тождество rot(grad(S)) = 0, находим соотношение, которому должен удовлетворять лучевой вектор :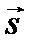

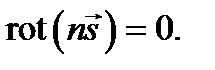
Выберем небольшой прямоугольный контур 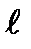(рис. 7.2 а), стороны P ₁ Q ₁ и P ₂ Q ₂ которого параллельны поверхности раздела Т двух сред, a P ₁ P ₂ и Q ₁ Q ₂ перпендикулярны Т. Пусть 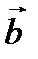– единичный вектор нормали к плоскости контура. Умножим скалярно на 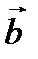и проинтегрируем по площади s, ограниченной контуром 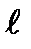. Поток ротора по теореме Стокса преобразуется в интеграл по контуру 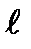: 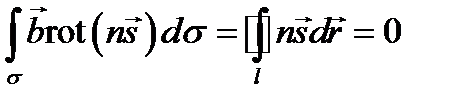. Переходя к пределу, когда длины сторон P ₁ P ₂ и Q ₁ Q ₂ стремятся к нулю, получим

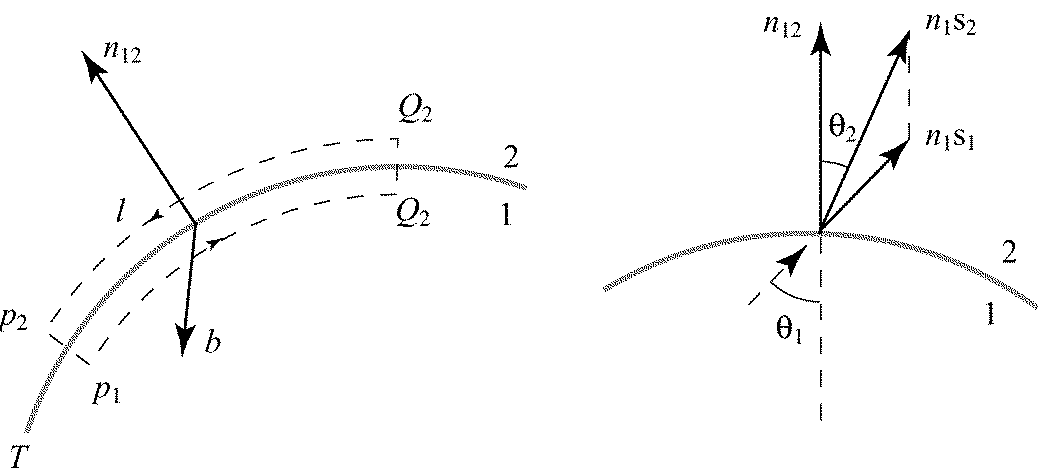
Р и с. 7.2

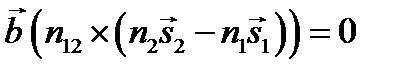
или

,

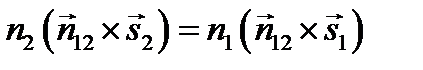где 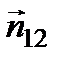– единичный вектор нормали к поверхности раздела Т. Из формулы следует, что преломленный луч лежит в плоскости падения (плоскости, образованной падающим лучом и нормалью 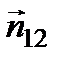(рис. 7.2 б)), а синусы углов падения и преломления связаны соотношением n ₂sin q ₂ = n ₁sin q ₁. Как и следовало ожидать, закон преломления, установленный для плоских волн на плоской границе раздела, в приближении геометрической оптики (l ₀ ® 0) справедлив для преломляющих поверхностей более общей формы. Фактически для этого достаточно, чтобы радиусы кривизны волновой поверхности падающей волны и поверхности раздела были велики по сравнению с l ₀.

Нахождение траекторий лучей света в приближении геометрической оптики можно сформулировать как задачу вариационного исчисления, если воспользоваться принципом Ферма, согласно которому свет распространяется между двумя точками по такому пути, который требует для прохождения наименьшего времени. Принцип наикратчайшего оптического пути, сформулированный Пьером Ферма в середине XVII в., можно получить как следствие основного уравнения геометрической оптики. Рассмотрим некоторую область с показателем преломления 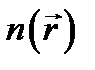, через каждую точку которой проходит только один луч (например, от точечного источника), т. е. эти лучи в рассматриваемой области не пересекаются. Пусть точки A и B (рис.7.3 а) лежат на одном луче. Используя уравнение , вычислим следующий интеграл вдоль произвольной кривой, соединяющей точки A и B: .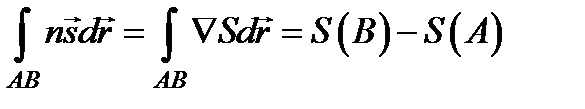

Этот интеграл равен разности значений эйконала в точках A и B и, следовательно, не зависит от пути интегрирования (интегральный инвариант Лагранжа). Очевидно, что , поэтому ,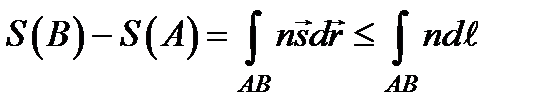

а) б)

Р и с. 7.3

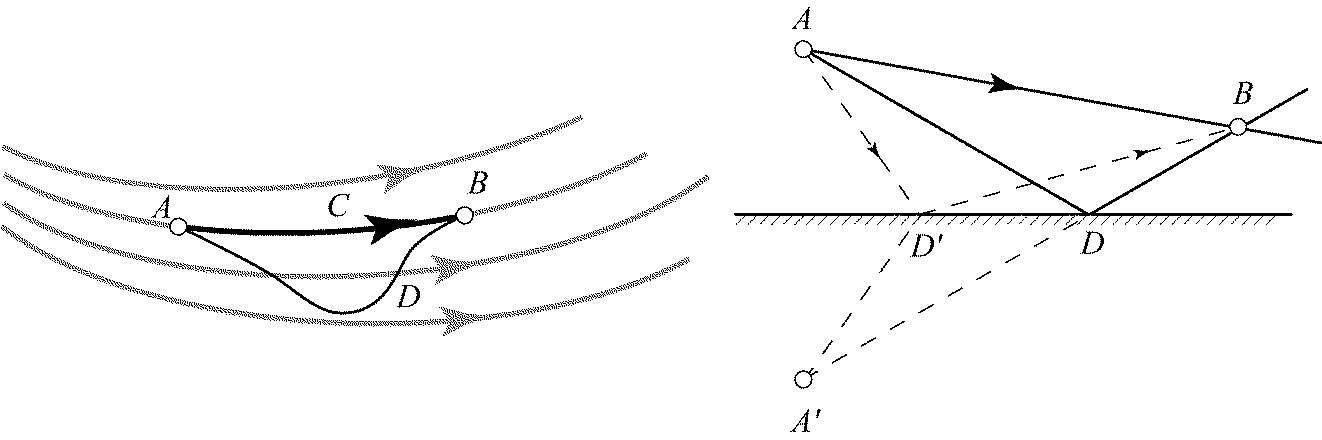
причем знак равенства справедлив только в том случае, когда направления векторов 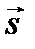и 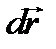совпадают в каждой точке рассматриваемой кривой, т.е. когда она представляет собой реальный луч (АСВ на рис. 7.3 а). Для любой другой кривой, соединяющей точки А и В (например, ADB на рис. 7.3 а), правая часть, называемая оптической длиной пути, оказывается больше, чем для реального луча АСВ. Поскольку 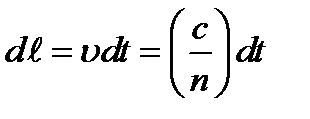, оптическая длина равна произведению c на время, которое требуется свету для прохождения вдоль этой кривой. Таким образом, свет между А и В распространяется по тому пути, который требует наименьшего времени.

В приведенном выше доказательстве было использовано предположение о том, что через каждую точку рассматриваемой области проходит только один луч. Это условие во многих практически важных случаях не выполняется. Например, при отражении от зеркала света, испускаемого точечным источником А, через любую точку В проходят два луча (рис. 7.3 б). Чтобы охватить подобные случаи, принцип Ферма можно сформулировать в более слабой форме, но применимой в более широкой области: реальный луч отличается от остальных кривых, соединяющих две заданные точки, тем, что соответствующая ему оптическая длина имеет стационарное значение, т. е. малое изменение траектории (например, точки падения на зеркало; рис. 7.3 б) не приводит в первом порядке к изменению оптической длины. Эта формулировка вполне достаточна для практических приложений, ибо для нахождения луча можно ограничиться сравнением оптических длин для воображаемых путей, которые проходят бесконечно близко от действительного.

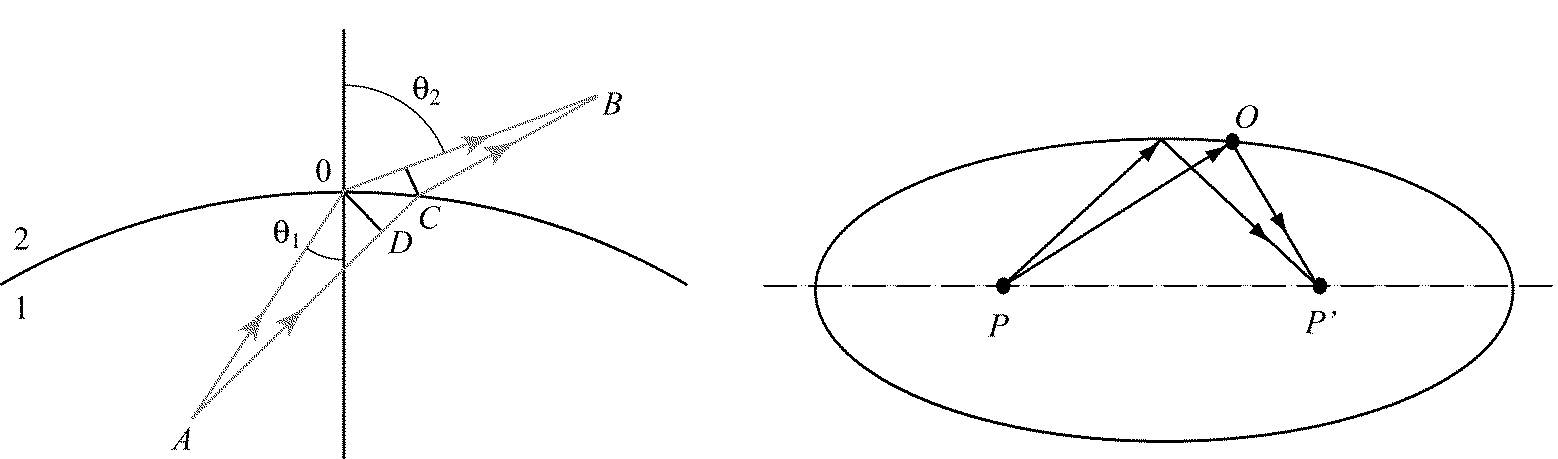
Проиллюстрируем применение принципа Ферма на примере преломления луча на границе однородных сред. Пусть АОВ – истинный путь света из A в B (рис. 7.4). Тогда при малом изменении траектории – смещении точки преломления из O в C – оптическая длина в первом приближении должна остаться неизменной. Оптический путь в среде 1 увеличивается на n ₁| DC | = n ₁| OC |sin q ₁, в среде 2 – уменьшается на n ₂| OE | = n ₂| OC |sin q ₂. Приравнивая эти величины, опять получаем закон преломления: .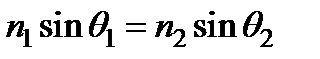

Если пучок лучей, выходящих из какой-либо точки P, после отражений, преломлений на границах или искривлений в неоднородной среде сходится в точке Р ', то Р' называется действительным фокусом геометрического схождения лучей. Его можно рассматривать как оптическое изображение точки Р. Изображение называют мнимым, если в Р' пересекаются не сами лучи, а их продолжения, проведенные в направлении, противоположном распространению света. Если источник Р и его изображение Р' поменять местами, то форма всех лучей останется без изменения и лишь их направление изменится на противоположное (принцип обратимости). Поэтому точки Р и Р ' называются сопряжёнными. Когда все лучи пересекаются строго в одной точке Р' – изображение называется стигматическим (точечным). Пучок лучей, выходящих из одной точки или сходящихся в одну точку, называется гомоцентрическим.

В соответствии с принципом Ферма оптическая длина всех лучей между сопряженными точками одинакова. В качестве примера рассмотрим зеркало в форме эллипсоида вращения (рис. 7.5). Сумма расстояний | РО |+| ОР '| от его фокусов до точки О имеет одно и то же значение при любом положении точки О на его поверхности. Если в один из фокусов поместить точечный источник, в другом фокусе пучок отраженных от зеркала лучей образует стигматическое изображение источника. Исходящие из фокуса эллипсоида гомоцентрические пучки лучей в результате отражения превращаются снова в гомоцентрические. Совершенно аналогично в фокусе параболического зеркала образуется стигматическое изображение находящегося на оси параболоида бесконечно удаленного точечного источника (параболоид можно рассматривать как предельный случай эллипсоида, когда второй его фокус удаляется в бесконечность). Такие параболические зеркала используются в астрономических телескопах-рефлекторах.

Эти примеры преобразования пучков света иллюстрируют скорее исключения, чем общее правило: обычно при отражении или преломлении пучок утрачивает свойство гомоцентричности и не образует стигматического изображения точечного источника. Например, отраженные параболическим зеркалом лучи от бесконечно удаленного источника, не лежащего на оси зеркала, пересекаются не в одной точке, а в некоторой ее окрестности, что ухудшает качество изображения. Используемые на практике оптические системы состоят из линз и зеркал, преломляющие и отражающие поверхности которых, как правило, сферические или плоские. Ход приосевых лучей и образование изображений в центрированных оптических системах рассматриваются позже. Искажения изображений, связанные с нарушением гомоцентричности пучков, называются геометрическими или лучевыми аберрациями оптических систем. Зависимость показателя преломления от длины волны приводит к появлению хроматической аберрации. Неизбежные в принципе погрешности отображения можно уменьшить до разумных пределов, используя многолинзовые конструкции. В этом отношении инструментальная оптика достигла замечательных результатов.

Но даже в тех случаях, когда по законам геометрической оптики пучок лучей пересекается строго в одной точке, образование точечного изображения светящейся точки невозможно из-за дифракции света. Вблизи фокуса пучка лучей кривизна волновых поверхностей становится значительной. Изменение амплитуды волны здесь уже нельзя считать малыми на протяжении длины волны, т.е. условия применимости геометрической оптики не выполняются, и распределение интенсивности вблизи фокуса обусловлено волновой природой света. Волновые, или дифракционные, искажения определяют теоретический предел разрешающей способности оптических инструментов.

Date: 2015-08-06; view: 938; Нарушение авторских прав