Разделение движений в системах с большим коэффициентом

Большие коэффициенты применяются в системах ради высокой точности или форсирования (ускорения) процессов в некоторой части системы. С помощью большого коэффициента можно некоторую инерционность довести до нуля. Рассмотрим систему, которая описывается следующей системой уравнений:

где .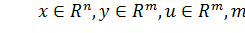

Подставим второе и третье уравнения для (17.1) в первое.

Будем полагать, что 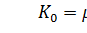, где K – матрица коэффициентов размером .

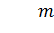Из-за наличия малого параметра μ в системе появляется большой коэффициент.

Тогда уравнение (17.2) может быть переписано так:

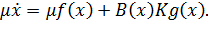
Фазовый портрет такой системы с форсированными процессами будет выглядеть как на рис. 17.1.

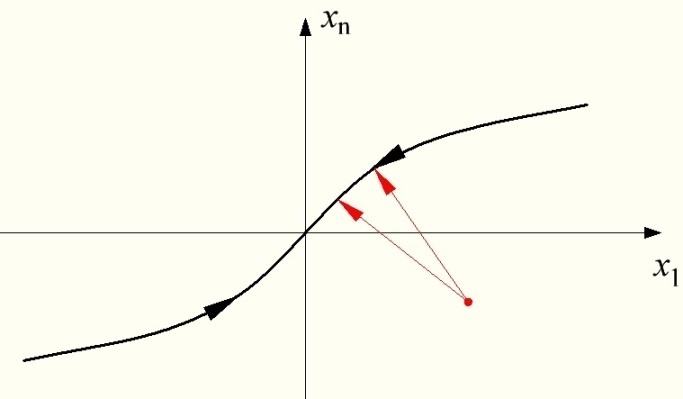
Рис. 17.1 Фазовый портрет системы с большим коэффициентом

Из-за большого множителя имеет место участок быстрых движений по всем координатами состояния, однако траектория движения изображающей точки не будет параллельна ни одной из осей.

Докажем теперь, что на поверхности 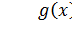движение будет медленным.

Продифференцируем по t тождество .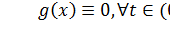

При условии, что 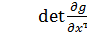выразим из (17.3) управление u.

где .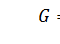

Подставим (17.4) в уравнение объекта (17.1).

(17.5) – уравнение медленных движений.

Из (17.5) видно, что движение системы определяется только свойствами объекта и поверхности 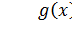, а, следовательно, не зависит от большого коэффициента

Предельный случай: если 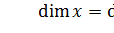, то 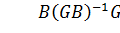, где Е – единичная матрица. Тогда . Таким образом, системы вырождается в точку.

Для получения уравнения быстрых движений вводится быстрое время 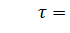, 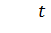. Тогда уравнение объекта примет вид:

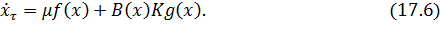
При μ→0 из уравнения (17.6) получаем подсистему быстрых движений в быстром времени:

Если ПБД (17.7) устойчива, то процессы будут сходиться к поверхности .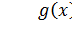

К сожалению, ПБД (17.7) является нелинейной и её сходимость к поверхности 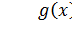необходимо проверять нелинейными методами. На практике устойчивость такой системы проще проверить экспериментально (то есть при помощи моделирования).

Разделение движений для данной системы можно применять и в стандартном виде:

Для (17.8) введем новую группу переменных для управляющего воздействия u.

Тогда из (17.8) с учетом (17.9) получим следующую систему:

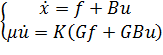
Date: 2015-07-27; view: 480; Нарушение авторских прав