
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Системы с реальным фильтром
|
|
Рассмотрим свойства системы с реальным дифференцирующим фильтром на рис. 13.1
| μ |
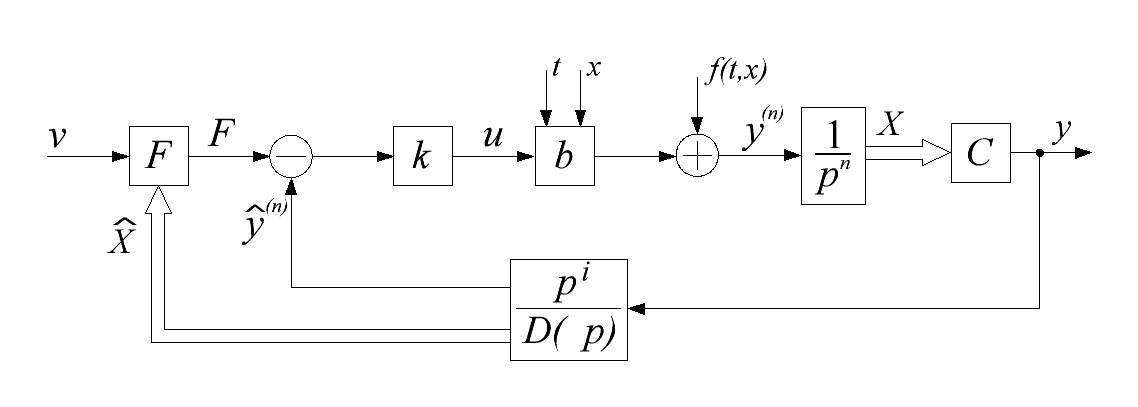
Рис. 13.1 Физическая схема системы с реальным дифференцированием (i =0,1,…, n)
В реальной схеме на рис. 13.1 не видно контура локализации. Чтобы увидеть этот контур необходимо в схеме «расщепить» фильтр на параллельные каналы и выделить канал со старшей производной.
| μ |
| μ |
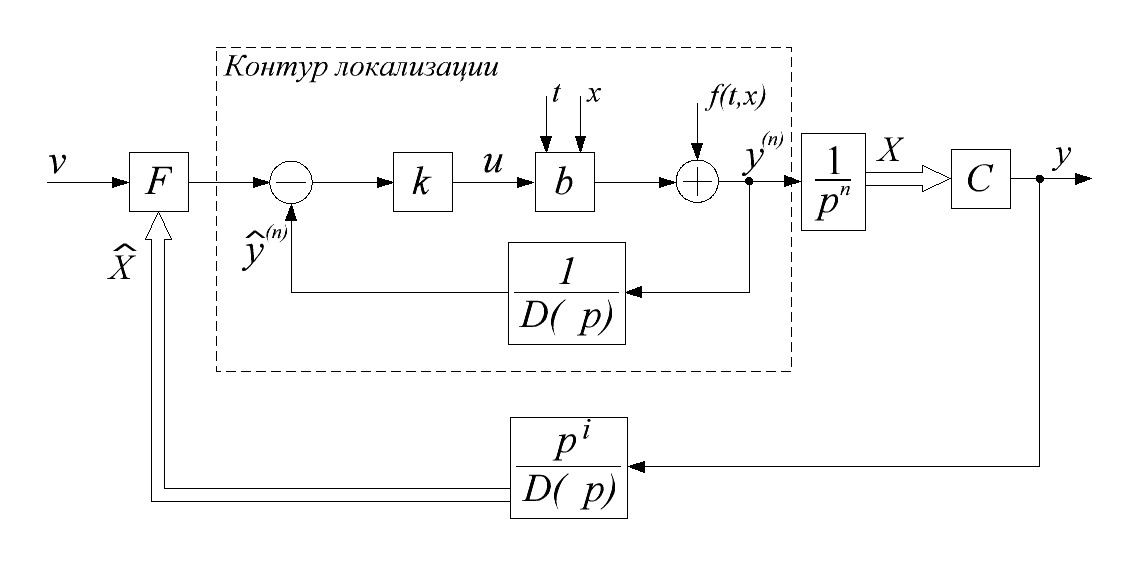
Рис. 13.2 Расчетная схема системы с реальным дифференцированием
В расчетной схеме 13.2 имеет место контур локализации. Поскольку этот контур быстрей рабочих процессов в системе, то его можно рассчитывать отдельно от всей системы.
| μ |
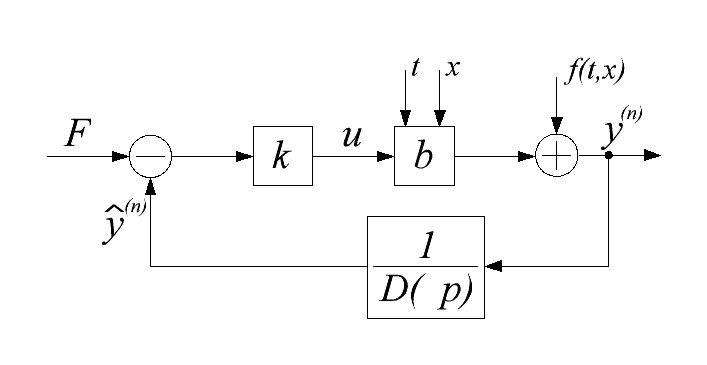
Рис. 13.3 Контур локализации
Контур на рис. 13.3 является линейным с нестационарным коэффициентом b. Его динамика определяется фильтрующим полиномом 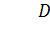 , коэффициентом k в некоторых случаях переменным коэффициентом b. Синтез (коррекцию) этого контура можно производить обычными линейными методами. Наиболее подходящий для этой цели – модальный метод.
, коэффициентом k в некоторых случаях переменным коэффициентом b. Синтез (коррекцию) этого контура можно производить обычными линейными методами. Наиболее подходящий для этой цели – модальный метод.
Характеристическое уравнение контура быстрых движений на рис. 13.3 имеет вид
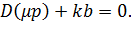
В реальных нелинейных системах расчет сводится к решению трех линейных задач:
1. Подбор линейного эталонного уравнения;
2. Подбор линейного дифференцирующего фильтра;
3. Коррекция линейного контура быстрых движений.
14. ПД – регулятор для нелинейного объекта
14.1 ПД – регулятор
В настоящее время все способы настройки ПД – регулятора предполагают, что объект линейный. Но можно показать, что и для нелинейного объекта первого порядка ПД – регулятор (и тем более ПИД - регулятор) полностью решает задачу подавления возмущений.
Рассмотрим пример и ПД – регулятором.
Имеем нелинейный, нестационарный объект первого порядка:

Необходимо, чтобы замкнутая система соответствовала эталонному характеристическому уравнению 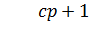
Закон управления: 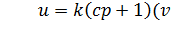 .
.
Смысл в том, что если 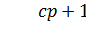 , то выражение (14.1) преобразуется следующим образом:
, то выражение (14.1) преобразуется следующим образом:
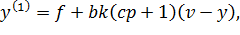
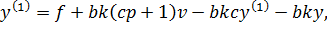
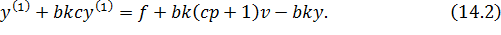
Разделим обе части уравнения (14.2) на bk.
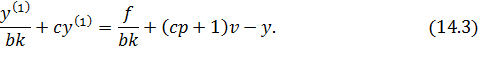
При bk →∞ уравнение (14.3) вырождается в следующее:
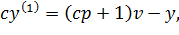
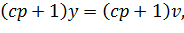

Таким образом, из уравнения (14.5) видно, что при большом коэффициенте усиления k ПД – регулятор в обычной системе для нелинейного, нестационарного объекта идеально решает задачу управления. Характеристическое уравнение системы в таком случае 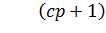
Недостаток:
1) В данной системе ПД – регулятор не может отработать скачкообразное изменение входа, так как для этого потребуется бесконечное управление.
Чтобы исключить этот недостаток, необходимо переставить форсирующее звено в обратную связь. Тогда закон управления будет иметь вид
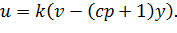
Преобразуем уравнение (14.1) в соответствии с новым законом управления.
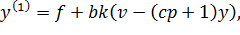
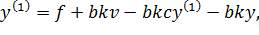
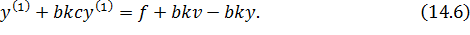
Разделим обе части уравнения (14.6) на bk.
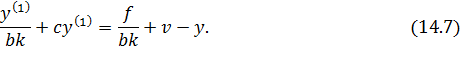
При bk →∞ уравнение (14.7) вырождается в следующее:

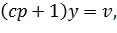

Таким образом, из уравнения (14.8) видно, что недостаток устранен, и данная система может отработать ступенчатое изменение выходного сигнала v. При увеличении коэффициента усиления k происходит подавление нелинейностей и нестационарностей. Однако в таком случае увеличивается влияние помех.
14.2 ПИД – регулятор
Рассмотрим полный ПИД – регулятор для нелинейного объекта первого порядка вида (14.1). Разделим ПИД – регулятор на два: регулятор статики и регулятор динамики.
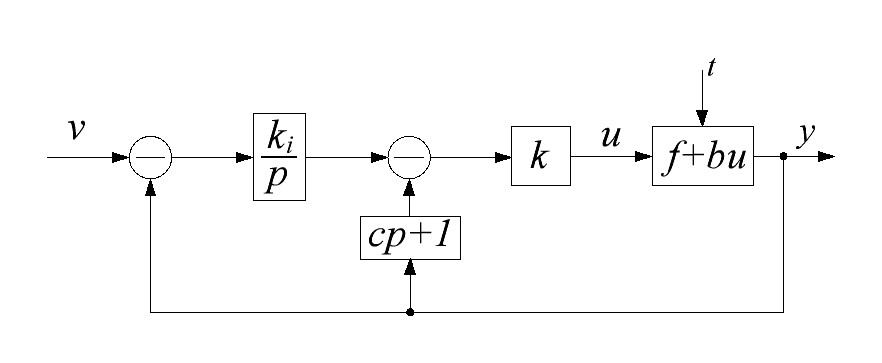
Рис. 14.1 Схема системы с ПИД – регулятором
В схеме на рис. 14.1  – регулятор статики, который устраняет статическую ошибку, k – коэффициент, позволяющий подавить возмущения,
– регулятор статики, который устраняет статическую ошибку, k – коэффициент, позволяющий подавить возмущения, 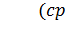 – форсирующее звено, с – задаваемая инерционность форсирующего звена.
– форсирующее звено, с – задаваемая инерционность форсирующего звена.
При достаточно больших значениях коэффициента усиления k параметры ki и c полностью определяют динамику системы. Обоснуем это высказывание математически.
Закону управления для системы (14.1) имеет вид:
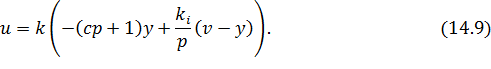
Преобразуем уравнение (14.1) в соответствии с законом управления (14.9).
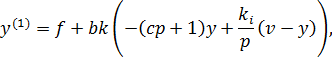
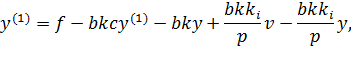
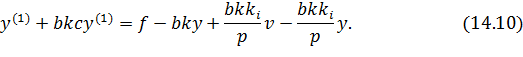
Разделим обе части уравнения (14.10) на bk.
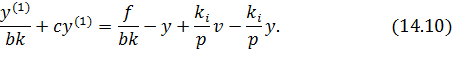
При bk →∞ уравнение (14.10) вырождается в следующее:
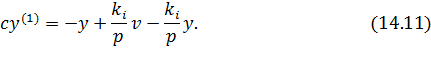
Продифференцируем уравнение (14.11) (то есть умножим всё на р).
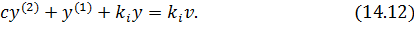
Если  , разделим уравнение (14.12) на
, разделим уравнение (14.12) на 
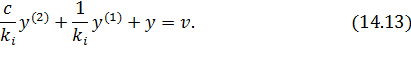
Получили дифференциальное уравнение второго порядка (14.13). Стандартный вид уравнения для системы второго порядка следующий: 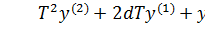 .
.
Тогда для выражения (14.13) имеем систему (14.14), состоящую из двух уравнений я двумя неизвестными:

Пример: Зададим T и d и найдем с и  Пусть T= 1 сек, d= 0,5. Тогда
Пусть T= 1 сек, d= 0,5. Тогда  , с= 1.
, с= 1.
Date: 2015-07-27; view: 413; Нарушение авторских прав