Одноканальные канонические системы

«Канонические» - типовые, типичные.

Уравнение канонических систем имеет вид

В (12.1) u, y ∈ R ¹, Х – вектор состояний, который состоит из n производных выходной переменной у.

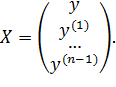
Особенность нелинейных объектов управления в том, что нелинейная характеристика f (t,X,u) никогда не известна точно. Явная зависимость нелинейной характеристики от времени обусловлена действием различных возмущений.

В отличие от линейных систем, для нелинейных систем требования к динамике и статике задаются не тремя параметрами (точность, быстродействие, демпфирование), а с помощью эталонного уравнения

где F – линейная функция.

Задача управления состоит в том, чтобы поведение объекта (12.1) соответствовало эталонному уравнению (12.2). Иначе говоря, необходимо подобрать такой закон управления u, чтобы выполнялось следующее равенство

Для того чтобы изобрести алгоритм управления, подробно рассмотрим свойства объекта.

В технических системах численные значения функции f (∙) всегда ограничены. Предполагается, что характеристика изменения функции f (∙) с течением времени меняется в рабочих пределах.

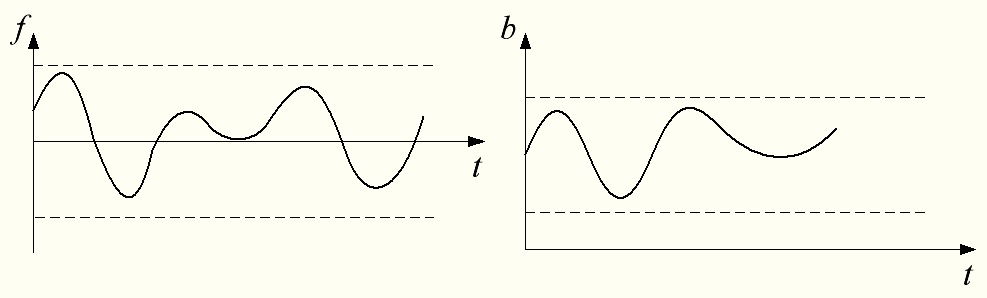
Рис. 12.1 Характер допустимых изменений значений нелинейной функции f (∙)

Следует отметить, что, так как функция f (∙) монотонно положительная, то с течением времени меняется положительной рабочей области.

Структурная схема, соответствующая уравнения (12.1) с ООС и коэффициентом k показана на рис. 12.2. Закон управления в такой системе формируется в виде .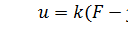

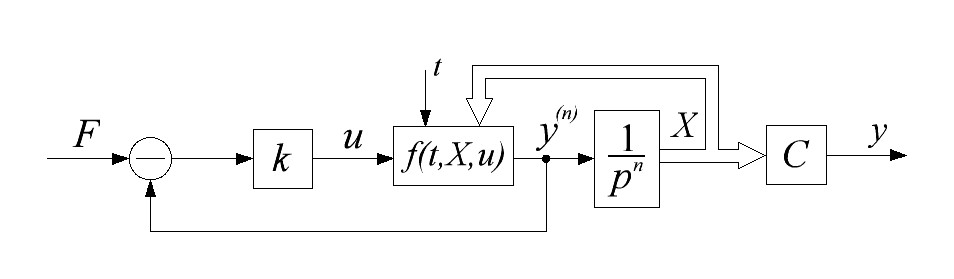
Рис. 12.2 Структурная схема системы

С помощью ООС по и коэффициента k подавляются все нелинейности и нестационарности, действующие на объект.

Рис. 12.3 Система со старшей производной в управлении

Контур 1 является безынерционным. В нем парируются все нелинейности и нестацонарности, и система получается инвариантной по отношению к возмущениям и нестационарностям. Блок С представляет собой матрица – строку и из всех координат состояния выделяет только выходную перемену у.

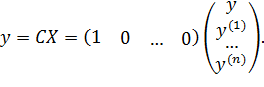
Недостаток:

1) Высокая чувствительность по отношению к помехам и большим значениям коэффициента k.

Пример: рассмотрим объект с аддитивным управлением

Закон управления имеет вид

Эталонное уравнение имеет вид (12.2).

Предположим, что можно вычислить точное управление .

1) Подставим изобретенный закон управления в уравнение объекта:

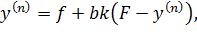
При k →∞ правая часть выражения (12.6) стремится к F. Таким образом, 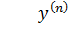, что соответствует эталонному уравнению.

2) Рассмотрим, к чему стремится управление u. Для этого в (12.5) подставим уравнение объекта (12.4).

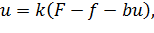
При k →∞ правая часть выражения (12.7) стремится к 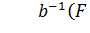. Таким образом, в пределе алгоритм управления дает точное значение управления :

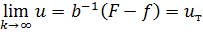
Рис. 12.4 Зависимость управления u от коэффициента усиления k

Из этого следует важное техническое свойство: при бесконечном значении коэффициента k управление u остается конечным в любой момент времени.

3) Рассмотрим действие помехи на управление.

При наличии помехи имеем следующий закон управления:

где .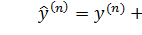

В (12.8) подставим уравнение объекта (12.4).

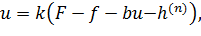
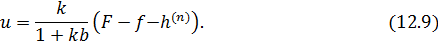
При k →∞ правая часть выражения (12.9) стремится к 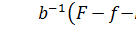. Таким образом, в пределе получаем следующее:

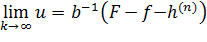
Вклад помехи в управлени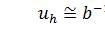е: , где - это управление, вызванное помехой. Опасность наличия помехи состоит в том, что по абсолютным значениям может стать больше 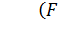. На практике такое происходит уже при двукратном дифференцировании. В таком случае помеха «забьет» тракт и система станет неработоспособной. Поэтому на высоких частотах нужно в полно мере использовать фильтрующие свойства дифференциаторов. Тогда влияние реальных помех измерения можно довести до допустимых значений даже при трехкратном дифференцировании. Технические свойства таких систем объясняются образованием локального контура, в котором подавляются действия нестационарностей.

Date: 2015-07-27; view: 380; Нарушение авторских прав