Метод разделения движений

Идея метода: пренебрежение малым параметром, но только по отношению к малым инерционностям в системе.

Рассмотрим следующую систему уравнений:

где 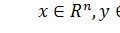, μ – малый параметр, .

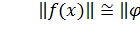Изобразим приблизительный фазовый портрет системы (16.1).

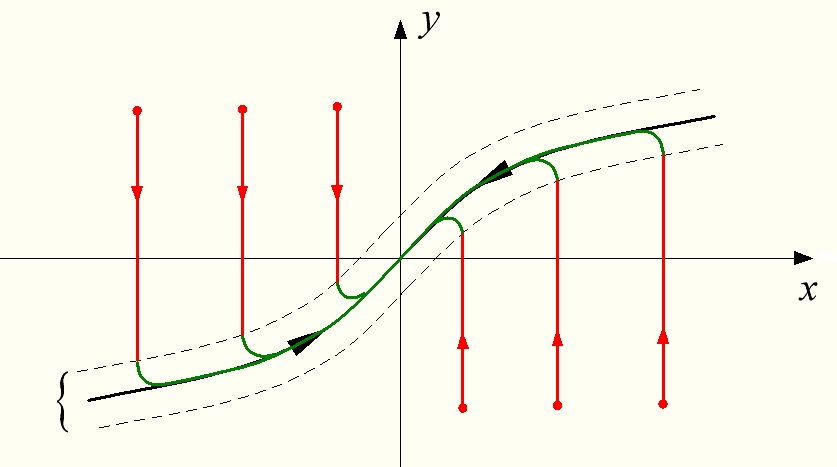
Рис. 16.1 Фазовый портрет системы (16.1)

Фазовый портрет на рис. 16.1 имеет два участка переходных процессов.

Участок 1 (красные линии) – участок быстрых движений, где 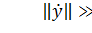при μ→0.

На этом участке изображающая точка быстро очерчивает траекторию движения до пограничного слоя.

Пограничный слой возникает вокруг поверхности 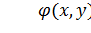. В нем векторы скорости и становятся соизмеримыми. Чем меньше значение μ, тем меньше толщина пограничного слоя.

Участок 2 (зеленые линии) – участок медленных движений.

На этом участке изображающая точка движется вдоль поверхности 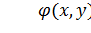. Для оценки скорости вдоль поверхности используется следующее выражение:

Продифференцируем выражение (16.2) по t.

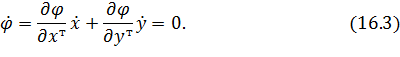
Выразим из уравнения (16.3) при условии, что :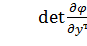

Подставим (16.1) в (16.4).

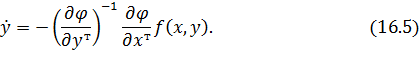
В итоге из уравнения (16.5) можно сделать вывод: при движении изображающей точки вдоль поверхности 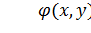векторы и соизмеримы.

На участке 2 уравнение движения можно упростить. По теореме об обращении неявных функций: если 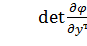, то 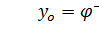. Теперь подставим это выражение в первое уравнение (16.1).

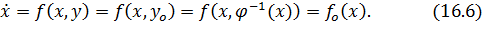
Уравнение (16.6) справедливо только для поверхности .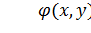

Получим уравнение для быстрого участка процесса. Для этого введем новое время 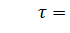, где t – старое время. То есть «замедлим» быстрые движения. Теперь применим новое время к системе уравнений (16.1) при условии, что

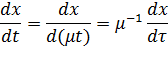
Тогда получим новую систему уравнений:

Если μ→0, то система уравнений (16.7) примет вид

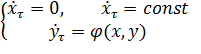
Перейдем теперь обратно к старому времени t.

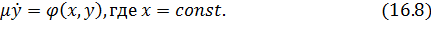
Уравнение (16.8) – автономное уравнение или уравнение быстрых движений. Оно описывает участок 1 переходного процесса, при этом у должен стремиться к поверхности .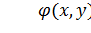

Date: 2015-07-27; view: 860; Нарушение авторских прав