Квадратные корни из комплексных чисел

Квадратным корнем из комплексного числа 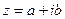является такое числ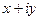о , что 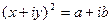. Пусть 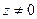, тогда 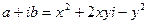, или

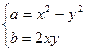(7.2.1)

Возведем оба уравнения системы в квадрат и прибавим к первому второе: 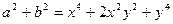, отсюда 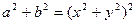. Так как 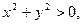то 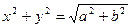. Рассмотрим это уравнение вместе с первым уравнением системы (7.2.1)

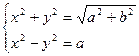
Отсюда

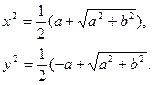(7.2.2)

Каждое из этих двух соотношение дает два разных значения для x и y. Комбинируя их, мы можем получить четыре различных комплексных числа, однако не все они удовлетворяют системе (7.2.1): как видно из второго уравнения, знаки x и y должны совпадать, если b >0, и различаться, если b <0. Если b= 0, т.е. число z вещественное, то либо x, либо y равно нулю. В предыдущем пункте мы видели, что корень n -ой степени из произвольного ненулевого комплексного числа имеет ровно n значений. Таким образом, для

n = 2 эти значения получаются по формулам (7.2.2), скомбинированным с приведенным правилом выбора знака.

Пример. Найти все значения .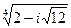

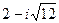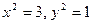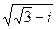Сначала найдем все значения корня квадратного из . Из (7.2.2) имеем . Так как мнимая часть подкоренного числа отрицательна, то . Вычислим теперь . Получаем 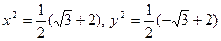. Отсюда =

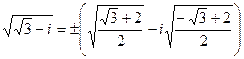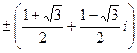= . Далее заметим, что значения корня 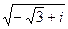отличаются от соответствующих значений корня 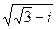множителем i.

Ответ: , .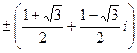

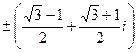Date: 2015-07-02; view: 1122; Нарушение авторских прав