Комплексная плоскость

То, что действительные числа изображаются точками (или векторами) числовой оси, известно даже людям, далеким от математики: достаточно представить обычную линейку с делениями. Геометрическое представление - в виде точек и векторов, но уже не прямой, а плоскости, - существует и для комплексных чисел.

Алгебраическая форма комплексного числа 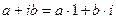как суммы кратных двух единиц – действительной 1 и мнимой 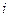- наводит на мысль о линейной комбинации с действительными коэффициентами двух векторов, изображающих соответственно единицу и мнимую единицу. Если первый – это единичный вектор действительной оси, то второй естественно вообразить направленным под углом к первому. Величину этого угла определим, исходя из следующих соображений. Умножение векторов на -1 означает их поворот на угол 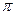без изменения длины. Поскольку умножение на -1 равносильно двукратному умножению на 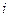, за изображение мнимой единицы естественно принять единичный вектор, перпендикулярный действительной оси и для определенности тот, который повернут относительно вектора, изображающего единицу, на угол против часовой стрелки.

В результате комплексные числа получают изображение в виде векторов координатной плоскости, а их запись 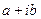обретает смысл разложения 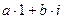изображающих векторов по ортонормированному базису 1, .

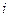Из формул предыдущего параграфа следует, что сложению и вычитанию комплексных чисел отвечают сложение и вычитание представляющих их векторов; то же относится к умножению и делению комплексных чисел на действительные. Что же касается умножения и деления комплексных чисел друг на друга, то хотя прямых аналогов эти операции не имеют, придать им определенный геометрический смысл можно (см. далее п. 3).

Число 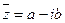называется комплексно сопряженным для 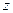. Имеем . Непосредственно проверяются равенства 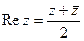, , 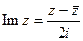а также свойство перестановочности операции комплексного сопряжения с четырьмя действиями:

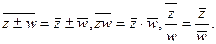
Векторы, изображающие комплексно-сопряженные числа 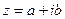и 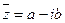, симметричны относительно действительной оси, говоря другими словами, операции 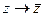соответствует зеркальное отражение векторов плоскости относительно действительной оси.

Способ изображения комплексных чисел на координатной плоскости был изобретен на рубеже XVIII и XIX вв. скандинавским математиком и землемером Весселем (Wessel, 1745-1818) и французским математиком Арганом (Argand, 1768-1822) и долгое время назывался диаграммами Аргана. Сейчас геометрический образ системы комплексных чисел принято называть комплексной плоскостью и обозначать тем же символом C, что и саму систему.

Date: 2015-07-02; view: 723; Нарушение авторских прав