Корни из единицы

По формуле (5.2) корнями n -ой степени из 1=cos 0 + i sin 0 являются числа

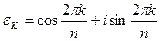(7.1.1)

Примеры:

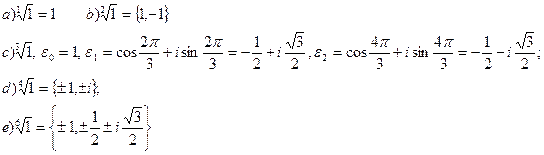
Пример. Вычислить 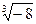. Решение можно провести по аналогии с Примерами из пункта 5, но здесь рассмотрим другой способ, основанный на свойстве, доказанном в утверждении пункта 5. Одним из частных значений 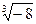является -2. С другой стороны, 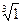имеет значения: 1, 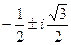. Поэтому все значения 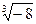исчерпываются тремя числами: -2, .

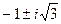Пример. Найти сумму всех корней n -ой степени из 1.

При n =1 сумма равна 1. При n >1 из (7.1.1) непосредственно следует, что 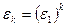, поэтому искомая сумма есть сумма геометрической прогрессии:

,

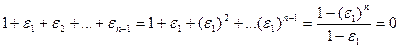т.к. .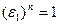

Утверждение1. Произведение и частное любых двух значений корня n-ой степени из 1 является корнем n-ой степени из 1.

Доказательство. Пусть 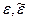некоторые значения корня n -ой степени из 1, тогда 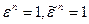, следовательно, 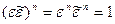и 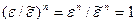, таким образом, являются значениями корня n -ой степени из 1.□

Будем называть первообразным корень 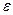n -ой степени из 1, если для любого натурального m<n (т.е. не является корнем из единицы никакой меньшей степени). В данном случае говорят также, что 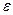принадлежит показателю n. Из определения сразу вытекает, что произвольное число 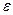может принадлежать лишь одному показателю. Легко видеть, что

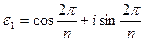
является первообразным корнем.

Утверждение 2. Для того, чтобы корень n -ой степени из 1 являлся первообразным, необходимо и достаточно, чтобы величины

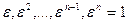(7.1.2)

исчерпывали все значения .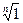

Замечание. Утверждение о том, что величины (7.1.2) исчерпывают все значения корня n -ой степени из 1 эквивалентно тому, что они попарно различны.

Доказательство. Необходимость. Предположим противное: среди величин (7.1.2) нашлось две равных, например, 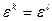для некоторых натуральных k,l,

Причем 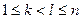. Тогда 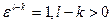, следовательно, 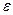не является первообразным.

Достаточность. Так как величины (7.1.2) исчерпывают все значения корня n -ой степени из 1, то, в частности, 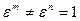, для всякого натурального m<n, следовательно, 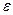- первообразный. □

Утверждение 3. Пусть 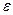- первообразный корень n -ой степени из 1, тогда для того, чтобы 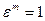, необходимо и достаточно, чтобы m было кратно n.

Доказательство.Необходимость. Разделим m с остатком на n: m=np+r для некоторых натуральных p и r (), поэтому

.

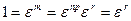Итак, 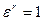. Так как 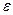- первообразный и , то r =0.

Достаточность. Имеем m=np, следовательно, .□

Следствие. Если корень 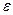m -ой степени из 1 принадлежит показателю n, то m кратно n.

Утверждение 3. Пусть 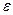- первообразный корень n -ой степени из 1, тогда для того, чтобы 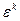был также первообразным n -ой степени, необходимо и достаточно, чтобы НОД(n,k)=1.

Доказательство. Необходимость. Предположим противное: 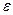и 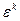- первообразные, однако НОД(n,k)= d >1. Имеем 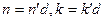для некоторых натуральных 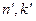, причем, так как d >1, то 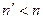. Однако

.

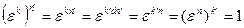Так как 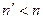, то 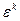не является первообразным корнем.

Достаточность. Предположим теперь, что 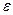- первообразный корень, НОД(n,k)=1, однако 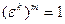для некоторого натурального m<n (т.е. 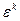не является первообразным). Из утверждения 2 следует, что km кратно n, однако НОД(n,k)=1, поэтому m кратно n, что невозможно, так как m<n. □

Следствие (критерий). Величина

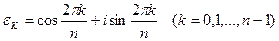
является первообразным корнем n -ой степени из 1 тогда и только тогда, когда НОД(n,k)=1.

Для доказательства достаточно применить утверждение 3 к первообразному корню .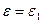

Пример. Найдем первообразные корни из 1 степени

a) 1, ответ:1

b) 2, один первообразный корень: ;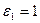

c) 3, два первообразных корня: ;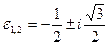

d) 4, два первообразных корня: ;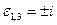

e) 6, два первообразных корня: ;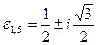

f) 8, выпишем все натуральные числа, не превосходящие 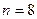и взаимно простые с ним: 1, 3, 5, 7; первообразными корнями являются величины

Из утверждения 3 следует, что число первообразных корней n -ой степени из 1 совпадает с количеством 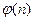натуральных чисел, не превосходящих n и взаимно простых с ним. Функция 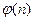называется функцией Эйлера.

Будем называть круговым многочленом показателя n, или многочленом деления круга выражение вида:

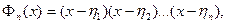
где 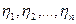- первообразные корни n -ой степени из 1.

Пример 7.5.

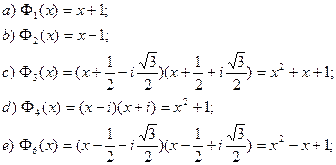
Утверждение. Справедливо равенство

(произведение берется по всем натуральным делителям m числа n).

Доказательство. Чтобы перечислить все корни n -ой степени из 1, воспользуемся следующей процедурой. Для каждого делителя m числа n выпишем все корни, принадлежащие показателю m. Из утверждения 2 следует, что таким образом мы перечислим все корни n -ой степени из 1 и каждый по одному разу. И наше утверждение теперь следует из разложения:

□

Пример. Выпишем , .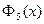

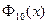a) Делителями n = 5 являются числа 1 и 5, поэтому 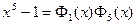, отсюда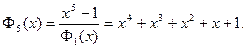

b) Делителями n = 10 являются числа 1, 2, 5, 10. Поэтому 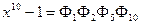, отсюда

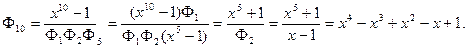
Date: 2015-07-02; view: 10262; Нарушение авторских прав