Теорема Гаусса о разрешимости алгебраических уравнений

Многочленом (полиномом или рациональной функцией) n -ой степени называется функция вида

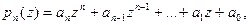(6.1)

где 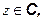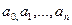- коэффициенты (вообще говоря, комплексные), причем

.

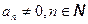Уравнение

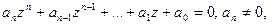(6.2)

называется алгебраическим уравнением n-ой степени. Число 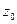, для которого 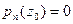, называется корнем многочлена (6.1) или уравнения (6.2).

Теорема Гаусса (“ основная теорема алгебры ”). Всякий многочлен ненулевой степени имеет по крайней мере один корень (вообще говоря, комплексный).

После опубликования Гауссом в 1799 году первого доказательства этой теоремы было найдено много других, и почти все они не являются алгебраическими по сути, а используют факты и методы теории функций комплексного переменного. По этой причине название “основная теорема алгебры” не слишком удачно, к тому же оно сужает представление о современном состоянии этого раздела математики.

Далее, число 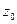является корнем многочлена 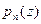в том и только том случае, когда 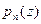делится без остатка на бином 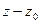, т.е.

,

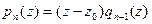где 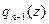- многочлен (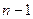)-ой степени. Если 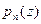делится без остатка на 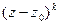, , 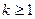но не делится на 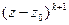, то 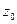называется корнем кратности k многочлена 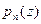; при этом

,

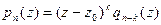где .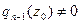

Теорема Гаусса можем быть уточнена следующим образом: многочлен

n-ой степени имеет ровно n корней, если каждый корень считать столько раз, какова его кратность.

Если коэффициенты многочлена (5.1) действительные числа и 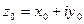- его комплексный корень, то сопряженное число 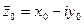- также корень этого многочлена, причем корн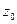и и 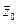имеют одинаковую кратность.

Пусть многочлен 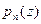имеет корни 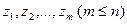кратностей, соответственно, 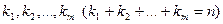. Тогда его можно разложить на линейные множители, т.е. справедливо тождество

.

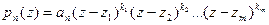Если при этом коэффициенты многочлена – действительные числа, то, объединяя скобки, соответствующие комплексно сопряженным корням, можно разложить этот многочлен в произведение линейных и квадратных множителей с действительными коэффициентами.

Пример. Найти корни многочлена 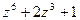и разложить его на множители. Заметим, что 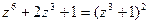. Поэтому корнями данного многочлена являются корни третьей степени из -1:

.

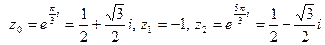При этом каждый корень имеет кратность k=2. Разложение этого многочлена на линейные множители имеет вид

.

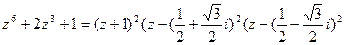Объединяя последние две скобки в один сомножитель, получим разложение на множители с действительными коэффициентами

.

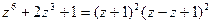Date: 2015-07-02; view: 3591; Нарушение авторских прав