Кубические уравнения с действительными коэффициентами

Пусть в уравнении (7.3.1) 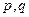- действительные числа. В зависимости от знака выражения 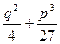в формулах Кардано (7.3.7) приходится вычислять корень квадратный либо из положительного, любо из нулевого, либо из отрицательного (действительного) числа. Рассмотрим каждый из этих случаев.

1) 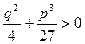. Под знаком кубического радикала в (7.3.7) стоят действительные числа. Вещественные значения этих корней дадут действительный корень 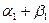. Два других корня, вычисленных по формулам (7.3.8), очевидно, будут взаимно сопряженными комплексными (см. пример 7.8).

2) 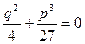. В этом случае 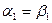, поэтому 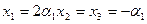. Все корни действительные.

3) 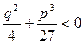(так называемый “неприводимый случай”). Пусть

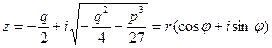
(в данном случае радикал означает арифметическое значение корня). Определим

модуль :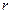

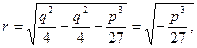
и аргумент :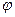

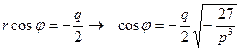
Из формул Кардано (7.3.7) следует, что

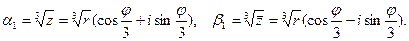
Легко проверить, что 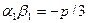, поэтому по формулам (7.3.8) получаем:

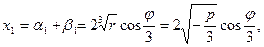
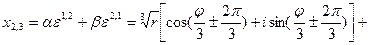
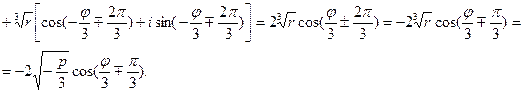
Итак, в “неприводимом случае” все три корня уравнения вещественные и различные и могут быть найдены по формулам:

(7.3.9)

где .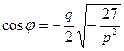

(так называемое “тригонометрическое” решение).

Заметим, что в данном случае, несмотря на то, что все три корня действительные, нам не удалось их выразить через радикалы от действительных же чисел: в формулах (7.3.7) приходится извлекать кубический корень из комплексного (не действительного) числа, а в (7.3.9) встречаются трансцендентные функции. Можно сказать, что в общем случае (т.е. для уравнения с буквенными коэффициентами) это невозможно, хотя в частных примерах иногда удается представить вещественные корни кубического уравнения через радикалы от действительных чисел (см. примеры ниже).

Пример.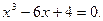

По формулам (7.3.7) получаем

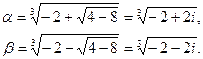
Здесь кубический корень удается извлечь точно. Например, 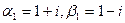. Прямой подстановкой убеждаемся, что (7.3.5) выполнено. Решения:

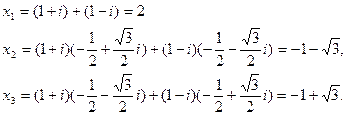
Пример. .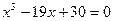

По формулам (7.3.9) получаем (приближенные вычисления с точностью до 4 значащих цифр):

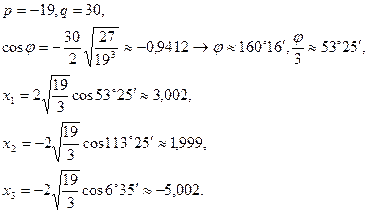
Легко проверить, что точными значениями решений уравнения являются целые числа 3, 2, -5.

Уравнения четвертой степени. Опишем способ Феррари (L.Ferrari,1545) для решения уравнения четвертой степени.

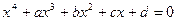(7.3.10)

Для произвольного значения параметра 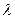уравнение (7.3.10) можно представить в виде:

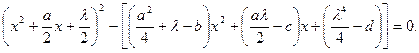(7.3.11)

Подберем 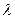так, чтобы выражение в квадратных скобках было квадратом двучлена, зависящего от 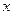. Для этого необходимо приравнять к нулю дискриминант этого выражения:

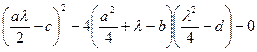. (7.3.12)

Таким образом, взяв любой корень уравнения (7.3.12), мы можем разложить левую часть (7.3.11) на линейные множители и тем самым отыскать корни исходного уравнения.

Вспомогательное кубическое уравнение (7.3.12) называется резольвентой.

Пример.

Резольвента имеет вид:

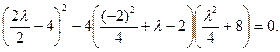
После раскрытия скобок и приведения подобных получаем:

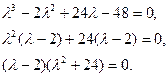
Одним из корней является 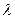=2. Воспользовавшись (7.3.11), левую часть исходного уравнения запишем в виде:

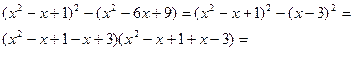
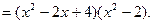
Раскладывая на линейные множители, получаем следующие корни:

.

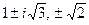Уравнения высших степеней. Мы видели, что корни алгебраического уравнения степени не выше 4 с буквенными коэффициентами можно выразить через коэффициенты этого уравнения при помощи конечного числа действий сложения, вычитания, умножения, деления и извлечения корня (говорят, что общее уравнение степени не выше 4 разрешимо в радикалах). Н.Абель (N.Abel) в 1826 году показал, что для алгебраических уравнений степени выше 4 этого сделать нельзя, иными словами, общее уравнение степени 5 и выше неразрешимо в радикалах. Результат Абеля не исключал возможности, что корни каждого конкретного уравнения (с числовыми коэффициентами) степени выше 4 выражаются с помощью некоторой комбинации арифметических операций и операций извлечения корня над коэффициентами исходного уравнения. Уравнения любой степени частных видов решаются в радикалах

(например, двучленное уравнение 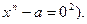Полное решение вопроса о том, при каких условиях алгебраическое уравнение разрешимо в радикалах было получено Э.Галуа (E.Galois) в 1830 г. Из результатов Галуа, например, следует, что для любой степени выше 4 найдутся уравнения с рациональными (и даже целыми) коэффициентами, неразрешимые в радикалах. Простым примером такого уравнения может служить .

Пример. Выразить в радикалах .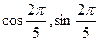

Число 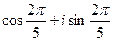является первообразным корнем 5-ой степени из 1 и поэтому одним из решений уравнения 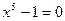или 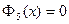. Таким образом, задача сводится к разысканию решений уравнения 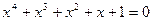. Это уравнение возвратное. Так как 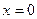не является его корнем, то мы можем записать:

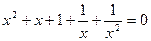(7.3.13)

или

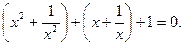
Пусть

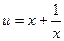, (7.2.14)

тогда 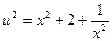и (7.3.13) примет вид 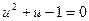. Корни последнего уравнения: 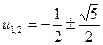. Теперь из (7.2.14) имеем:

Очевидно, 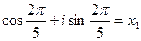. Таким образом,

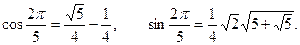
Пример. Составить алгебраическое уравнение с целыми коэффициентами, корнем которого является длина стороны правильного 14-угольника, вписанного в круг радиуса 1.

Обозначим сторону 14-угольника через d. Легко видеть, что . Пусть

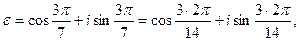
тогда . Заметим, что 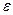является первообразным корнем 14-ой степени из 1 и поэтому корнем кругового многочлена

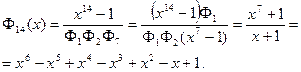
Разделив уравнение 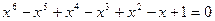на 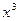, получим

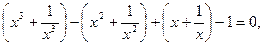
или

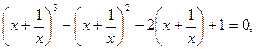
т.е. 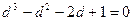. Это и есть искомое уравнение.

Date: 2015-07-02; view: 1811; Нарушение авторских прав