Уравнения второй, третьей и четвертой степени

Квадратные уравнения. Уравнением второй степени называется уравнени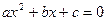е , где 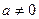. Делением его на a получим уравнение, равносильное данному:

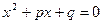(7.3.1)

Для его решения воспользуемся способом выделения полного квадрата. В правой части имеем:

.

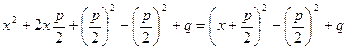Уравнение примет вид

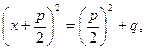или .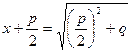

Квадратный корень в последней формуле имеет два значения, отличающиеся знаком. Итак, уравнение (7.3.1) имеет в общем случае два решения

.

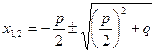Пример.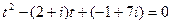

.

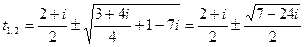Для нахождения всех значений квадратного корня воспользуемся методами из предыдущего раздела:

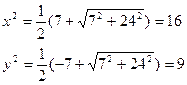
Отсюда 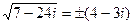, следовательно,

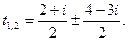
Итак, .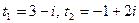

Кубические уравнения. Уравнение третьей степени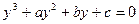

после замены 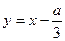преобразуется в виду:

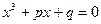(7.3.2)

Решение будем искать в виде

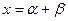, (7.3.3)

где 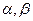- некоторые комплексные числа, связанные помимо (7.3.3) соотношением, которое мы определим ниже. После подстановки (7.3.3) в (7.3.2) получаем:

,

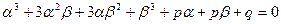или

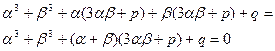(7.3.4)

Пусть

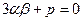, (7.3.5)

тогда (7.3.4) примет вид

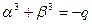(7.3.6)

Последнее равенство и (7.3.5.) после возведения в куб (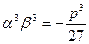) согласно теореме Виета позволяют утверждать, что 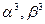являются решениями следующего квадратного уравнения

,

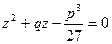поэтому

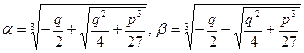. (7.3.7)

Среди всевозможных комбинаций 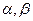необходимо выбрать лишь те, которые удовлетворяют условию (7.3.5). Легко видеть, что таким образом будет получено 3 решения (для каждого 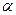из (7.3.5) можно определить единственное ). На практике из (7.3.7) выбирают какую-нибудь пару 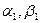, удовлетворяющую (7.3.5); решениями уравнения (7.3.2) являются числа

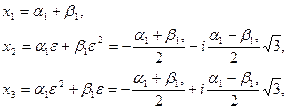(7.3.8)

где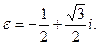

Выражения (7.3.7) и (7.3.8) называются формулами Кардано.

Пример. .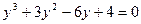

После подстановки 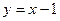исходное уравнение примет вид: .

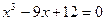Имеем:

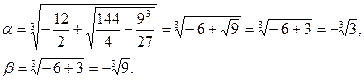
Поэтому

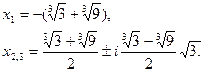
Отсюда

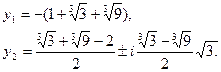
Date: 2015-07-02; view: 917; Нарушение авторских прав