Вычисление сумм и произведений с помощью комплексных чисел

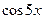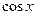Пример. Выразить через и .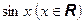

Пусть 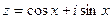. Найдем 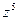двумя способами. По формуле бинома имеем:

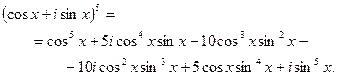
С другой стороны, по формуле Муавра: 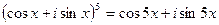. Приравнивая правые части полученных равенств и выделяя действительную часть, получаем:

.

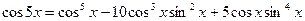Пример. Вычислить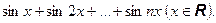

Пусть 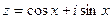, тогда рассматриваемая сумма есть мнимая часть выражения 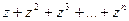, которое с помощью формулы для суммы геометрической прогрессии, формулы Муавра и простейших тригонометрических формул, преобразуется следующим образом:

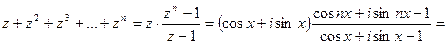
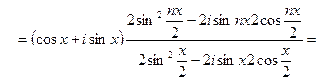
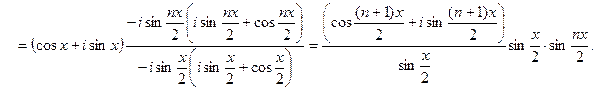Выделяя мнимую часть, получаем

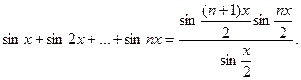
Выделяя действительную часть, можно получить

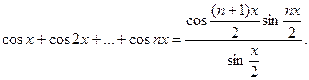
Пример. Вычислить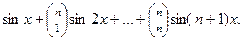

Пусть 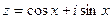. Преобразуем выражение, мнимая часть которого есть рассматриваемая сумма:

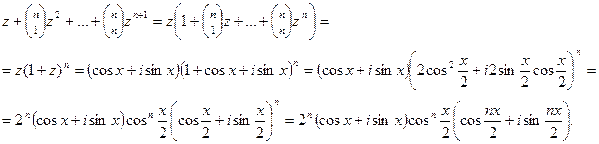Мы последовательно применили формулу бинома Ньютона, тригонометрические формулы двойного угла и, наконец, использовали формулу Муавра. Теперь, выделяя мнимую часть в последнем выражении, получаем

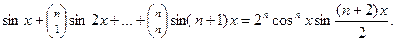
Пример. Вычислить .

Так как 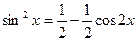, то

.

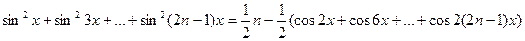Для вычисления суммы в круглых скобках положим 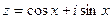и рассмотрим сумму

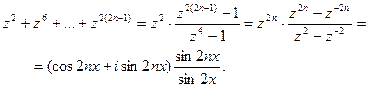
Выделяя действительную часть, получаем

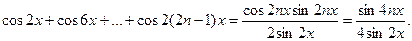
Поэтому

.

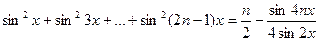Пример. Вычислить

a)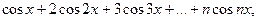

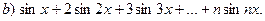
Пусть 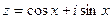. Первая сумма совпадает с действительной частью выражения 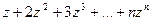, вторая сумма - с его мнимой частью. Для нахождения 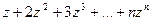рассмотрим произведение 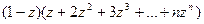, в котором, раскрывая скобки, получим

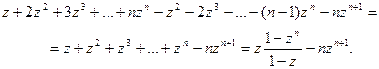
Следовательно,

.

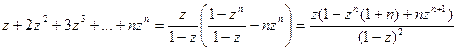Для отделения мнимой и действительной части в последнем выражении удобно ввести величину 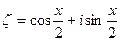, заметив, что 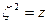. Итак,

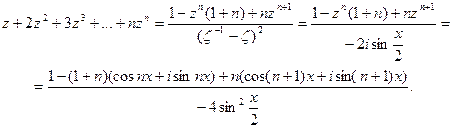
Выделяя действительную и мнимую части, соответственно, получаем

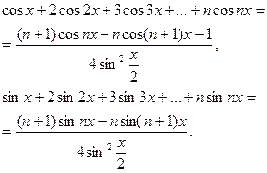
Пример. Выразить 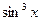через синусы кратных углов.

Пусть 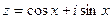, тогда нетрудно проверить, что 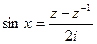и по формуле бинома Ньютона получаем

.

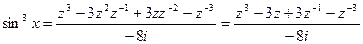Подставляя вместо z его выражение через x и приводя подобные, получаем

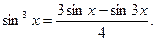
Пример. Выразить 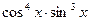через синусы кратных углов.

Пусть 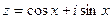, тогда 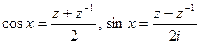и, следовательно,

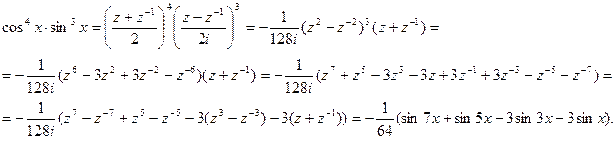Пример. Вычислить

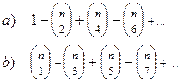
Разлагая 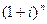по формуле бинома:

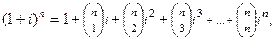
видим, что выражение а) есть действительная часть числа 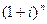, тогда как b) – его мнимая часть. Так как

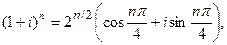
то

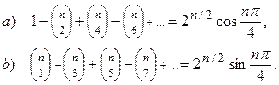
Пример. Вычислить

.

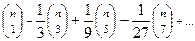Разложим 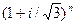по формуле бинома:

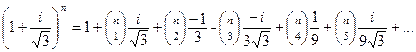
С другой стороны, по формуле Муавра:

.

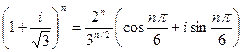Приравнивая мнимые части в обоих выражениях, получаем

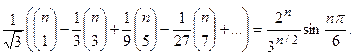
Отсюда

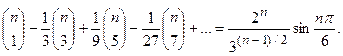
Пример. Вычислить

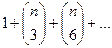
Рассмотрим выражени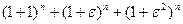е , где .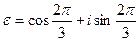

Раскладывая все три бинома и вынося за скобки общие биноминальные коэффициенты, получаем:

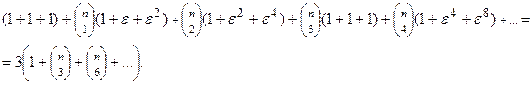
С другой стороны,

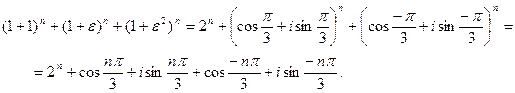
Следовательно,

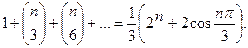
Date: 2015-07-02; view: 3425; Нарушение авторских прав