
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Показательная форма комплексного числа
|
|
Функция 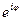 для любого действительного
для любого действительного 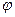 определяется формулой Эйлера:
определяется формулой Эйлера: 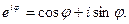 В частности,
В частности, 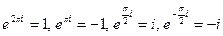 . Отметим, что
. Отметим, что 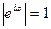 для любого
для любого 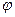 .
.
Показательная форма комплексного числа 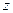
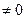 есть запись вида
есть запись вида 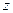 =
= 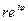 , где
, где 
Примеры: 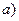 Если
Если  , то в показательной форме
, то в показательной форме 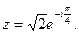
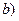 Представим в алгебраической форме число
Представим в алгебраической форме число 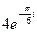 :
:

Для любого комплексного числа 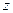 =
= 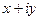 значение
значение 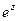 определяется равенством
определяется равенством
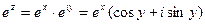 , (4.1)
, (4.1)
где 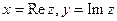 . Значения
. Значения 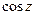 и
и 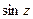 определяются равенствами
определяются равенствами
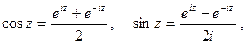 (4.2)
(4.2)
Имеем,
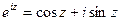 , для всех
, для всех 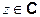 . (4.3)
. (4.3)
Формулы (4.1) - (4.3) называются формулами Эйлера.
Показательная форма комплексного числа удобна при умножении, делении и, самое главное, возведении в степень комплексных чисел. Пусть 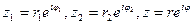 , тогда (см. п.3 Выводы):
, тогда (см. п.3 Выводы):
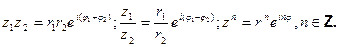
Последнее равенство – формула Муавра для комплексных чисел в показательной форме.
Пример. Вычислим 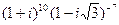 . Сначала перейдем к показательной форме комплексных чисел:
. Сначала перейдем к показательной форме комплексных чисел: 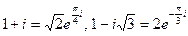 и воспользуемся формулой возведения в степень
и воспользуемся формулой возведения в степень 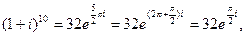
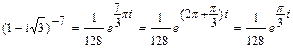 . Теперь воспользуемся формулой умножения чисел в показательной форме. Получим
. Теперь воспользуемся формулой умножения чисел в показательной форме. Получим 
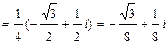 .
.
Пример.. Решим уравнение 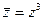 , используя показательную форму комплексных чисел. Уравнение принимает вид
, используя показательную форму комплексных чисел. Уравнение принимает вид
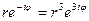 .
.
Отметим, что два числа, записанные в показательной форме равны тогда и только тогда, когда равны их модули, а аргументы отличаются на число, кратное 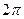 . Отсюда
. Отсюда 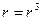 , т.е.
, т.е. 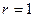 или
или 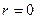 . В последнем случае
. В последнем случае 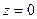 . Видно, что нуль является решением нашего уравнения. При
. Видно, что нуль является решением нашего уравнения. При 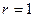 рассмотрим уравнение для аргументов
рассмотрим уравнение для аргументов 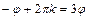 . Получаем
. Получаем 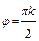 . Различные решения получаем только при
. Различные решения получаем только при 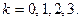 Это числа
Это числа 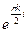 . Окончательные ответ: 0,
. Окончательные ответ: 0, 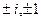 .
.
5. Извлечение корней из комплексных чисел
Пусть 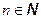 . Число
. Число 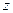 называется корнем
называется корнем 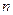 - ой степени из числа
- ой степени из числа 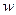 , если
, если 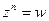 (обозначение
(обозначение 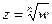 ). Поскольку уравнение
). Поскольку уравнение 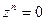 не имеет других решений, кроме
не имеет других решений, кроме 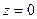 , то
, то 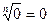 . Пусть
. Пусть  . В этом случае представим
. В этом случае представим 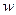 в тригонометрической форме:
в тригонометрической форме:
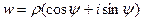 .
.
Воспользовавшись формулами Муавра, перепишем заданное равенство 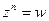 в виде
в виде
 .
.
Так как для ненулевого комплексного числа модуль определен однозначно, а аргумент с точностью до 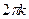 , где
, где 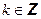 , то
, то 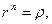 а
а 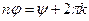 . Получаем
. Получаем
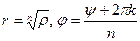
(для вычисления 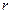 используется арифметическое значение корня
используется арифметическое значение корня 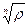 ). Итак, для произвольного
). Итак, для произвольного 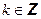 каждое из чисел
каждое из чисел
 (5.1)
(5.1)
является значением корня n -ой степени из числа 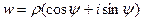 .
.
Выясним, есть ли среди чисел (5.1) совпадающие. Разделим произвольное 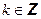 на n с остатком, т.е. представим k в виде
на n с остатком, т.е. представим k в виде 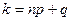
(напомним, что в данном случае p называется частным, а q – остатком, 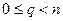 ). Подставляя это выражение для k в (5.1), получаем:
). Подставляя это выражение для k в (5.1), получаем:
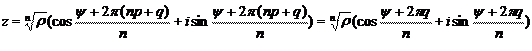
С другой стороны, при значениях k = 0,1, …, n -1 все числа в (5.1) различны: их аргументы отличаются на числа кратные 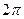 .
.
Подводя итог, получаем, что произвольное ненулевое комплексное число
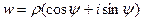 имеет n различных корней, которые можно получить по формуле
имеет n различных корней, которые можно получить по формуле
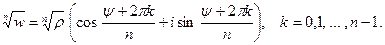 (5.2)
(5.2)
В показательной форме
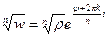 (5.2’)
(5.2’)
Заметим, что знак радикала в равенстве (5.2) имеет разный смысл: в правой части он означает арифметическое значение корня из положительного (действительного) числа, в левой – множество всевозможных значений корня из комплексного числа.
Из (5.2) легко видеть, что на комплексной плоскости все значения корня находятся на одинаковом расстоянии 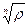 от точки 0, кроме того, угол с вершиной в 0 между направлениями на соседние значения корня постоянен и равен
от точки 0, кроме того, угол с вершиной в 0 между направлениями на соседние значения корня постоянен и равен 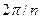 . Таким образом, точки комплексной плоскости, соответствующие всем значениям корня степени
. Таким образом, точки комплексной плоскости, соответствующие всем значениям корня степени 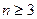 из одного и того же числа, находятся в вершинах правильного n -угольника. Это наблюдение позволяет по одному найденному корню уравнения
из одного и того же числа, находятся в вершинах правильного n -угольника. Это наблюдение позволяет по одному найденному корню уравнения 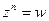 отыскать все остальные.
отыскать все остальные.
Примеры: 1) Найти 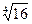 . Проведем решение для показательной формы заданного числа. Очевидно,
. Проведем решение для показательной формы заданного числа. Очевидно, 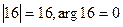 , т.о.
, т.о. 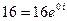 . По формуле (5.2’) имеем
. По формуле (5.2’) имеем 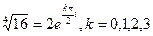 . Итак,
. Итак, 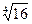 имеет следующие значения:
имеет следующие значения:
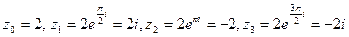 .
.
Зная одно из значений корня, остальные иногда, как в данном случае, проще найти геометрически. Легко проверить, что число 2 является одним из значений корня. Вписываем правильный четырехугольник, т.е. квадрат, одной из вершин которого является точка  , в окружность радиуса 2 с центром в нуле. Ясно, что остальными вершинами квадрата являются точки
, в окружность радиуса 2 с центром в нуле. Ясно, что остальными вершинами квадрата являются точки 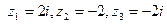 .
.
2) Найти 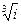 . Поскольку
. Поскольку 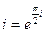 , то
, то 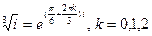 . И значения корня есть числа
. И значения корня есть числа 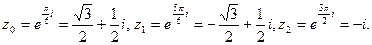
3) Найти 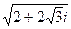 .
.
Последовательно получаем 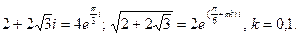
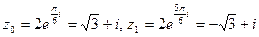 . Заметим, что, как и в вещественном случае, второе значение квадратного корня всегда можно получить из первого умножением на -1.
. Заметим, что, как и в вещественном случае, второе значение квадратного корня всегда можно получить из первого умножением на -1.
Справедливо следующее свойство: для ненулевых комплексных чисел 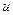 и
и 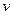 множество всех значений корня
множество всех значений корня 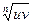 можно получить умножая произвольное значение корня
можно получить умножая произвольное значение корня 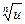 на все значения
на все значения 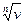 .
.
Date: 2015-07-02; view: 1299; Нарушение авторских прав