Тригонометрическая форма комплексного числа

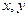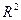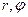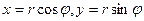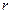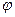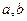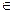
Вторыми по значению после декартовых (прямоугольных) координат на плоскости являются полярные координаты . Связанные с декартовыми соотношениями полярные координаты переносятся и на комплексную плоскость, но при этом меняется терминология: полярный радиус и полярный угол точки (или вектора) () 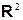называют соответственно модулем и аргументом комплексного числа 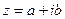с использованием обозначений , .

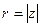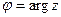Геометрически модуль комплексного числа есть длина вектора, представляющего это число на комплексной плоскости (или по другому, модуль равен расстоянию от 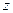до начала координат 0). Таким образом, 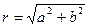. Далее, 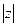=0 тогда и только тогда, когда 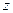=0. Приведем так называемые неравенства треугольника:

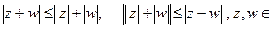C.

Аргумент ненулевого комплексного числа 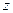(обозначение 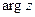) есть выраженная в радианах (или градусах) величина угла 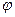, который образует вектор, изображающий 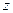, с действительной осью комплексной плоскости (положительным значениям углов соответствует их отсчет против часовой стрелки). Значение 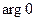не определено. Для любого ненулевого 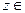C аргумент определяется с точностью до слагаемого, кратного .

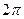Очевидно, по паре 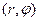комплексное число определяется однозначно.

Запись ненулевого комплексного числа 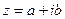в виде

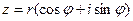(3.1)

называется тригонометрической формой комплексного числа .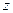

Примеры:

1) 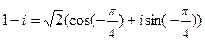. Отметим, что запись 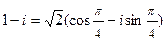также возможна, но она не является тригонометрической формой числа ;

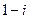2) -2 = ;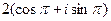

3) 1 = ;

4) .

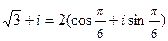В правых частях каждого из этих равенств к значению аргумента может быть добавлено любое целое кратное .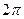

Чтобы учесть все значения аргумента комплексного числа 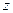, используют запись 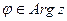, придавая символу 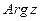смысл множества чисел вида 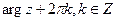, где 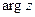- одно из значений аргумента числа 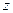. Под 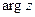обычно подразумевают так называемое главное значение выделяемое неравенствами 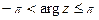(иногда ).

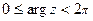Ноль тригонометрической формы не имеет.

Запись комплексных чисел в тригонометрической форме раскрывает геометрический смысл их умножения и деления. А именно, пусть 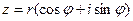, 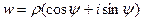. Тогда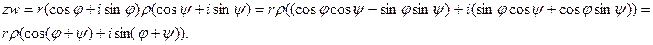 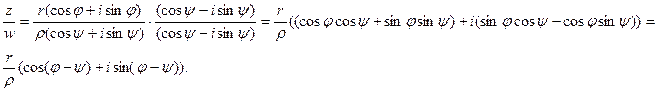Выводы:

1. При умножении ненулевых комплексных чисел их модули перемножаются, а аргументы складываются:

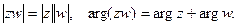
2. Модуль частного комплексных чисел равен частному их модулей, а аргумент – разности их аргументов:

(равенства для аргументов всюду считаются выполненными с точностью до слагаемых, кратных 2 ).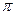

3. Для любого комплексного числа 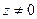и любого целого числа 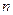выполняются соотношения

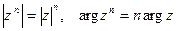
(второе, с точностью до слагаемого, кратных 2 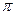); их запись в виде

,

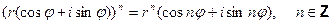называют формулой Муавра (A. De Moivre,1736).

4. В геометрической интерпретации произведению ненулевых чисел 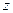и 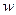соответствует точка, радиус-вектор которой получен поворотом радиус- вектора точки 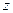на угол 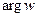и растяжением в 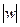раз. При делении 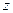на 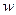радиус – вектор точки 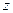поворачивается на угол - 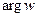и сжимается в 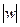раз.

Примеры: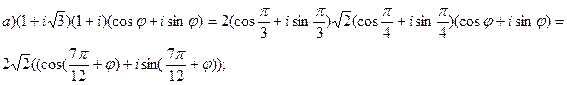

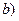
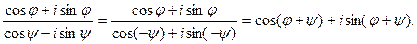
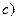Найдем тригонометрическую форму числа 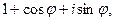если :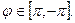

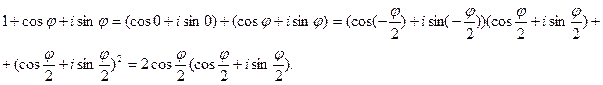
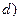Вычислим:

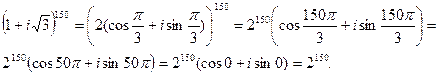
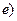Решим уравнение 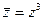. Запишем 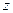в тригонометрической форме 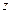= . Уравнение примет вид:

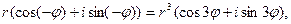откуда

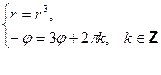; т.е.

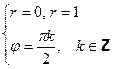
Последняя система дает решения: 0, .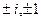

Date: 2015-07-02; view: 801; Нарушение авторских прав