
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задания для самостоятельной работы. Задание 1. Выполнить указанные действия, представив результат в алгебраической форме
|
|
Задание 1. Выполнить указанные действия, представив результат в алгебраической форме.
1.1. 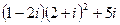
1.2. 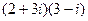
1.3. 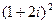
1.4. 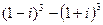
1.5. 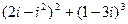
1.6. 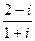
1.7. 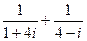
1.8. 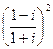
1.9. 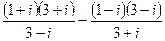
1.10. 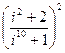
1.11. 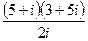
1.12. 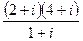
1.13. 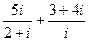
1.14. 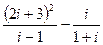
1.15 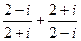
1.16. 
1.17. 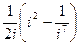
1.18. 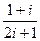
1.19. 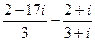
1.20. 

1.21 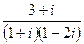
1.22. 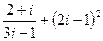
Найти число, сопряженное данному:
1.23. 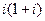
1.24. 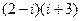
1.25. 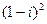
1.26. 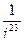
1.27. 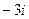
Задание 2. Комплексные числа представить в тригонометрической форме и изобразить точками на комплексной плоскости.
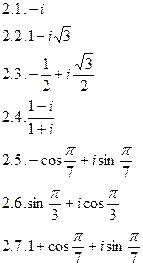
2.8. 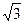
2.9. 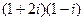
2.10. 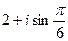
2.11. 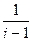
2.12. 
2.13. 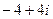
2.14. 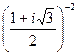
2.15. 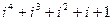
2.16. 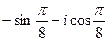
Вычислить, предварительно представив числа в тригонометрической форме,
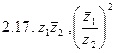 , если
, если 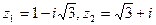
2.18. 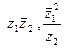 , если
, если 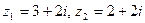
2.19. 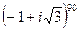 2.20.
2.20. 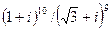 2.21.
2.21. 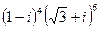
Представить числа в алгебраической форме
2.22. 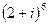 2.23.
2.23. 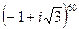 2.24.
2.24. 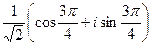
2.25. 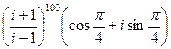 2.26.
2.26. 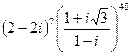
Решить уравнения
2.27. 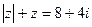 2.28.
2.28. 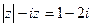 2.29.
2.29. 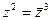
Задание 3. Выяснить геометрический смысл следующих преобразований
3.1. 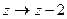
3.2. 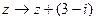
3.3. 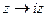
3.4. 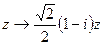
3.5. 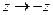
3.6. 
3.7. 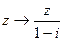
3.8. 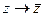
Дать геометрическое описание всех точек комплексной плоскости, удовлетворяющих следующим условиям:
3.9. 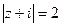 . 3.11.
. 3.11. 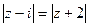 .
.
3.10. 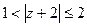 . 3.12.
. 3.12. 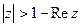 .
.
Задание 4. Найти все значения корней
4.1. 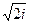 4.7.
4.7. 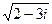
4.2. 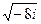 4.8.
4.8. 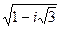
4.3. 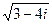 4.9.
4.9. 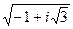
4.4. 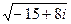 4.10.
4.10. 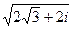
4.5. 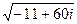 4.11.
4.11. 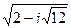
4.6. 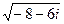 4.12.
4.12. 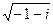
Вычислить
4.13. 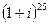 4.15.
4.15. 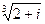
4.16. 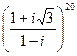 4.17.
4.17. 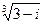
4.18. 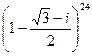 4.22.
4.22. 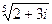
4.19. 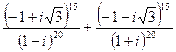 4.23.
4.23. 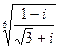
4.20. 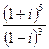 4.24.
4.24. 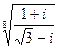
4.21. 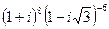 4.25.
4.25. 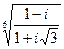
4.26. 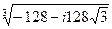
Задание 6. Выразить через 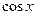 и
и 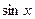
6.1. 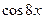 6.5.
6.5. 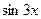
6.2. 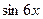 6.6.
6.6. 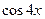
6.3. 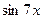 6.7.
6.7. 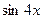
6.4. 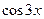 6.8.
6.8. 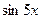
6.9. Выразить 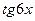 через
через 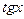 .
.
Вычислить суммы
6.10. 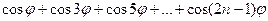
6.11. 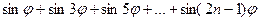
6.12. 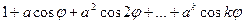
Задание 7. Решить уравнения
7.1. 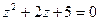 7.7.
7.7. 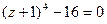
7.2. 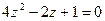 7.8.
7.8. 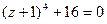
7.3 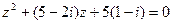 7.9.
7.9. 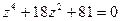
7.4. 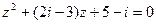 7.10.
7.10. 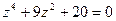

7.5. 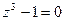 7.11.
7.11. 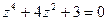
7.6. 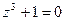 7.12.
7.12. 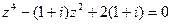
7.13. 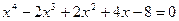
7.14. 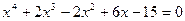
7.15. 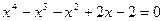
7.16. 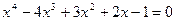
7.17. 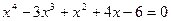
7.18. 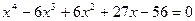
7.19. 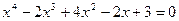
7.20. 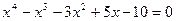
7.21. 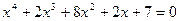
7.22. 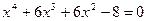
7.23. 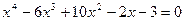
7.24. 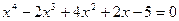
Литература
1. Волковыский М.И., Лунц Г.Л., Араманович И.Г. Сборник задач по теории
функций комплексного переменного. М.: Наука, 1975.
2. Евграфов М.А. (ред.). Сборник задач по теории аналитических функций.
М.: Наука, 1969.
3. Краснов М.Л., Киселев А.И., Макаренко Г.И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. М.: Наука, 1981.
4. Лаврентьев М.А., Шабат Б.В. Методы теории функции комплексного
переменного. М.: Наука, 1973.
5. Привалов И.И. Введение в теорию функций комплексного переменного. М.: Наука, 1997.
6. Соломенцев Е.Д. Функции комплексного переменного и их применение,
Учебное пособие. М.: Высшая школа, 1988
7..Сидоров Ю.В., Федорюк М.В., Шабунин М.И. Лекции по теории функций
комплексного переменного. М.: Наука, 1982.
Содержание
1. Комплексные числа: определение, операции сложения и
умножения.
2. Комплексная плоскость. Модуль и аргумент комплексного числа.
Операции комплексного сопряжения и деления.
3. Тригонометрическая и показательная формы.
4. Формулы Эйлера. Формула Муавра.
5. Извлечение корней из комплексных чисел.
6. Теорема Гаусса о разрешимости алгебраических уравнений. Разложение
алгебраического многочлена на множители.
7. Задачи.
7.1. Корни из единицы.
7.2. Квадратные корни из комплексных чисел
7.3.Уравнения второй, третьей и четвертой степени.
7.4. Вычисление сумм и произведений с помощью
комплексных чисел.
8. Задания для самостоятельной работы.
Date: 2015-07-02; view: 1515; Нарушение авторских прав