
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Комплексные числа: определение, операции сложения и умножения
|
|
Кафедра высшей математики
Аналитическая геометрия и линейная алгебра
Н.А.Фаркова
Комплексные числа
УДК 517.53
Комплексные числа. Методическая разработка по курсу “Аналитическая геометрия и линейная алгебра” для студентов.
Составитель Н.А.Фаркова. – доцент кафедры высшая математика-2.
Методическая разработка предназначена для студентов 1-го курса, изучающих курс линейной алгебры и аналитической геометрии и содержит необходимый теоретический материал, упражнения и задания для самостоятельной работы студентов.
Составитель: Н.А.Фаркова, к.ф.-м.н., доцент кафедры высшей математики
Комплексные числа: определение, операции сложения и умножения
Комплексными числами называются всевозможные упорядоченные пары 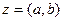 действительных чисел, для которых определены операции сложения и умножения следующим образом:
действительных чисел, для которых определены операции сложения и умножения следующим образом:
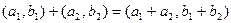 (1.1)
(1.1)
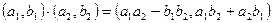 , (1.2)
, (1.2)
где 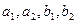 - произвольные действительные числа.
- произвольные действительные числа.
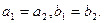 |
Два комплексных числа равны тогда и только тогда, когда
Множество всех комплексных чисел обозначается C.
Понятия “ больше” и “меньше ” для комплексных чисел не вводятся.
Действительные числа 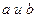 называются действительной и мнимой частями комплексного числа и обозначаются символами Re z и Im z соответственно. Комплексные числа
называются действительной и мнимой частями комплексного числа и обозначаются символами Re z и Im z соответственно. Комплексные числа 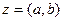 с нулевой мнимой частью
с нулевой мнимой частью
( ) - это действительные числа. Комплексные числа, не являющиеся действительными, получили название мнимых, а те их них, у которых действительная часть равна нулю
) - это действительные числа. Комплексные числа, не являющиеся действительными, получили название мнимых, а те их них, у которых действительная часть равна нулю 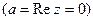 - чисто мнимых.
- чисто мнимых.
Для чисел 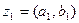 и
и 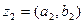 согласно формулам (1.1) и (1.2) имеем
согласно формулам (1.1) и (1.2) имеем
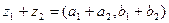
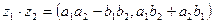 ,
,
Легко проверить, что операции сложения и умножения комплексных
чисел обладают следующими свойствами:
a) коммутативности 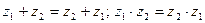
b) ассоциативность 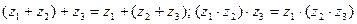
c) дистрибутивность 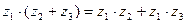
Нулем называется такое комплексное число 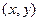 , что для произвольного числа (a,b) выполняется равенство
, что для произвольного числа (a,b) выполняется равенство 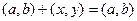 . Из определения получаем, что
. Из определения получаем, что 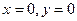 . Следовательно, нулем является пара (0,0).
. Следовательно, нулем является пара (0,0).
Числом, противоположным к (a,b) называется такая пара 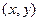 , что
, что 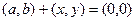 . Противоположное число обозначается -(a,b). Нетрудно видеть, что
. Противоположное число обозначается -(a,b). Нетрудно видеть, что
-(a,b) = (- a, -b). Разностью (или числом, полученным в результате вычитания) комплексных чисел (c,d) и (a,b) называется решение 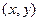 уравнения
уравнения 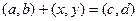 . Разность обозначается (c,d) -(a,b) и, очевидно, равна (c-a, d-b). Легко видеть, что разность (c,d) - (a,b) есть сумма (c,d) и числа, противоположного к (a,b), т.е. (c,d)- (a,b) = (c,d) +
. Разность обозначается (c,d) -(a,b) и, очевидно, равна (c-a, d-b). Легко видеть, что разность (c,d) - (a,b) есть сумма (c,d) и числа, противоположного к (a,b), т.е. (c,d)- (a,b) = (c,d) +
[- (a,b)].
Единицей называется такое комплексное число 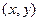 , что для произвольного числа (a,b) выполняется равенство
, что для произвольного числа (a,b) выполняется равенство 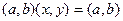 . Из определения произведения получаем
. Из определения произведения получаем
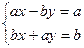
В случае если 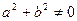 , т.е. (a,b)
, т.е. (a,b) 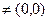 , имеем единственное решение предыдущей системы:
, имеем единственное решение предыдущей системы: 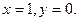 Таким образом,
Таким образом, 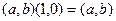 для любого
для любого  в том числе и для
в том числе и для 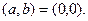 Следовательно, (1,0) – единица. Числом, обратным к
Следовательно, (1,0) – единица. Числом, обратным к  называется такая пара
называется такая пара 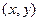 , что
, что 
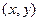 = (1,0). Обратное число обозначается
= (1,0). Обратное число обозначается 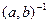 . В случае, когда
. В случае, когда
(a,b) 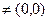 , система
, система
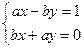
имеет единственное решение
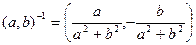 , (1.3)
, (1.3)
а в случае 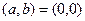 - неразрешима.
- неразрешима.
Частным (или числом, полученным в результате деления) комплексных чисел (c,d) и (a,b) называется решение 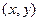 уравнения
уравнения 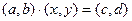 . Частное обозначается (c,d) /(a,b). Его можно получить из системы
. Частное обозначается (c,d) /(a,b). Его можно получить из системы
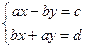 . (1.4)
. (1.4)
В случае 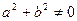 имеем:
имеем:
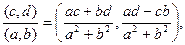 (1.5)
(1.5)
если же 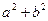 =0, то результат деления, как легко видеть из (1.4), не определен. Сравнивая (1.3) и (1.5), получаем, что частное (c,d) /(a,b) есть произведение (c,d) на величину, обратную к (a,b):
=0, то результат деления, как легко видеть из (1.4), не определен. Сравнивая (1.3) и (1.5), получаем, что частное (c,d) /(a,b) есть произведение (c,d) на величину, обратную к (a,b):
(c,d) /(a,b)= 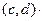
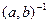 .
.
Обозначим через i и будем называть мнимой единицей число (0,1). Для i = (0,1) имеем i2 = i  i = (0
i = (0  0-1
0-1  1,0
1,0  1+1
1+1  0) = (-1,0) = -1, т.е.
0) = (-1,0) = -1, т.е.
i2 = -1 (1.6).
Заметим также, что
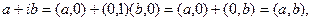
т.е. число 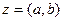 представимо в виде
представимо в виде 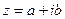 . Указанный вид называется алгебраической формой комплексного числа
. Указанный вид называется алгебраической формой комплексного числа 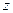 . Ее использование освобождает нас от заучивания правил арифметических операций (1.1) и (1.2): в силу (1.6) работать с комплексными числами можно как с алгебраическими двучленами, зависящими от символа i, с заменой, где необходимо, i2 на -1. Например, для нахождения произведения
. Ее использование освобождает нас от заучивания правил арифметических операций (1.1) и (1.2): в силу (1.6) работать с комплексными числами можно как с алгебраическими двучленами, зависящими от символа i, с заменой, где необходимо, i2 на -1. Например, для нахождения произведения 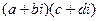 раскроем скобки и получим
раскроем скобки и получим 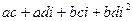 , так как i2 = -1, то
, так как i2 = -1, то 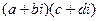 =
= 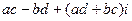 . Для нахождения частного
. Для нахождения частного 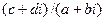 умножим числитель и знаменатель дроби на число
умножим числитель и знаменатель дроби на число 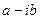 :
:
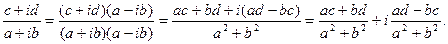
Упражнение. Проверьте, что
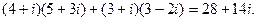
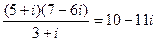 .
.
Date: 2015-07-02; view: 777; Нарушение авторских прав