
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Извлечение корня n-й степени из комплексного числа
|
|
Корнем n-ой степени из комплексного числа называется такое комплексное число w, которое, будучи возведено в степень n, даст число z, то есть
w = 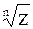 , если wn= z.
, если wn= z.
Корень n-ой степени из числа z = r(cos j + i sin j) имеет n значений, определяемых по формуле
w = 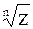 =
= 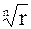 (cos(
(cos(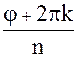 ) + i sin (
) + i sin (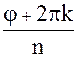 )) (10)
)) (10)
или w = 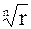
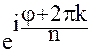 ,
,
где j - любое фиксированное значение аргумента, а 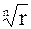 понимается в арифметическом смысле (как неотрицательное вещественное число); число k принимает n значений:
понимается в арифметическом смысле (как неотрицательное вещественное число); число k принимает n значений:
k = 0, 1, 2,..., n - 1.
Геометрически числа wk располагаются в вершинах правильного n-угольника, вписанного в круг радиуса 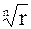 с центром в начале координат.
с центром в начале координат.
Примеры.
1. Найти все корни третьей степени из числа z = 1.
Решение. 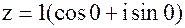
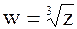
k=0; 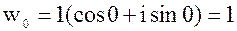
k=1; 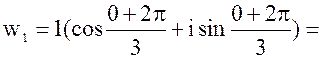
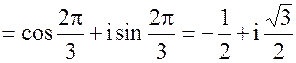
k=2; 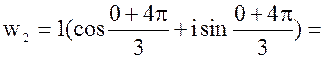
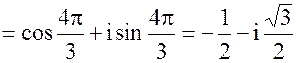
2. Решить уравнение x4 + 16 = 0
Решение:
x4 = -16; x = 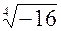 . Так как -16 = 16 (cos p +i sin p), то
. Так как -16 = 16 (cos p +i sin p), то
x = 2 (cos (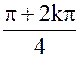 ) + i sin (
) + i sin (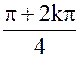 ));
));
k = 0; x0 = 2 (cos (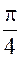 ) + i sin (
) + i sin (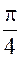 )) = 2 (
)) = 2 (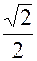 + i
+ i 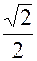 ) =
) = 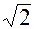 + i
+ i 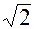 ;
;
k = 1; x1 = 2(cos (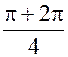 ) + i sin (
) + i sin (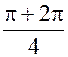 )) = 2 (-
)) = 2 (- 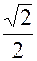 + i
+ i 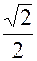 ) =
) =
= - 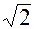 + i
+ i 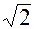 ;
;
k = 2; x2 = cos (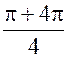 ) + i sin (
) + i sin (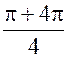 )) = 2 (-
)) = 2 (- 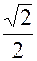 - i
- i 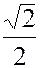 ) =
) =
= – 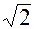 - i
- i 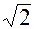 ;
;
k = 3; x3 = cos (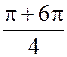 ) + i sin (
) + i sin (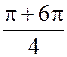 )) = 2 (
)) = 2 (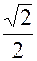 - i
- i 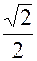 ) =
) =
= 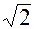 - i
- i 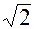 .
.
Варианты заданий.
5.1. Образец решения заданий.
Условия задач:
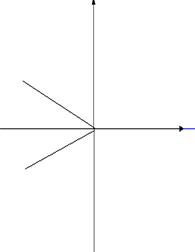
1. Дано комплексное число z. Построить точки z и 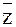 .
.
Найти |z|, | 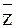 |, arg z, arg
|, arg z, arg 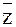 .
.
2. Найти вещественную и мнимую части данных комплексных чисел.
3. Найти все корни данных уравнений.
4. Найти такие вещественные x и y, чтобы выполнялось данное равенство.
5. Написать такое квадратное уравнение, для которого x1 является корнем.
6. Записать данное комплексное число в алгебраической, тригонометрической и показательной формах.
Примеры.
1. z = -8 + 4i
Решение:
| 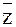 = -8 - 4i
|z| = | = -8 - 4i
|z| = | 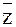 | = | = 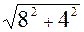 = = 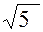 j = arg z tg j = -
j = arg z tg j = - 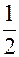 j = p - arctg
j = p - arctg 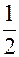 arg z @ 1530
arg
arg z @ 1530
arg 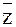 @ - 1530 @ - 1530
|
2. а) z = 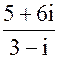
Решение:
z = 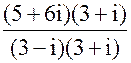 =
= 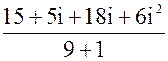 =
= 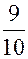 +
+ 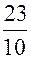 i;
i;
z = 0,9 + 2,3i; Re z = 0,9; Im z = 2,3
б) z = 4i153 - 2i122 + i20 - i7
Решение:
Так как i2 = -1, то i3 = -i, i4 = 1.
z = 4i152× i - 2i120× i2 + i20 - i4×i3 = 4i + 2 + 1 + i = 3 + 5i
Re z = 3 Im z = 5
в) z = 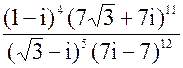
Решение:
z = 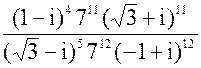 =
= 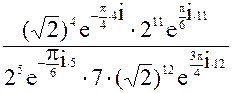 =
=
=  =
= 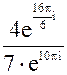 =
= 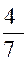 (cos
(cos 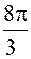 + i sin
+ i sin 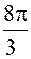 ) =
) =
= 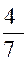 (cos
(cos 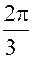 + i sin
+ i sin 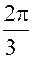 ) =
) = 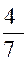 (-
(- 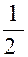 + i
+ i 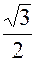 ) = -
) = - 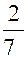 +
+ 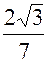 i
i
Re z = - 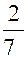 Im z =
Im z = 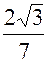
3. а) x2 - 8x + 41 = 0
Решение:
x1,2 = 4 ± 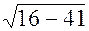 = 4 ±
= 4 ± 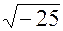 = 4 ± 5i
= 4 ± 5i
б) x3 - 1000 = 0
Решение:
x3 = 1000 = 1000(cos 0 + sin 0)
xk = 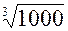 (cos
(cos 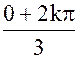 + i sin
+ i sin 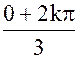 )
)
k = 0; x0 = 10 (cos 0 + i sin 0) = 10
k = 1; x1 = 10 (cos 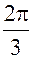 + i sin
+ i sin 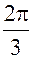 ) = 10 (-
) = 10 (- 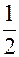 +
+ 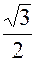 i) = -5 + 5i
i) = -5 + 5i 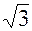
k = 2; x2 = 10 (cos 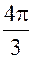 + i sin
+ i sin 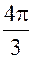 ) = 10 (-
) = 10 (- 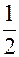 -
- 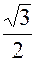 i) = -5 - 5i
i) = -5 - 5i 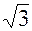
4. 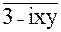 = x + y +2i
= x + y +2i
Решение:
3 + ixy = x + y + 2i
Приравняем вещественные и мнимые части:
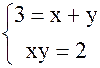
x = 1, y = 2 или x = 2, y = 1
5. x1 = 1 - 6i
Решение:
x2 = 1 + 6i
Если квадратное уравнение имеет вид x2 + px + q = 0, то
x1 + x2 = - p x1 + x2 = 2
x1×x2 = q x1×x2 = (1 - 6i)(1 + 6i) = 1 + 36 = 37
Получили уравнение: x2 - 2x + 37 = 0
6. z = 1 + sin 2320 + i cos 2320
Решение:
По формулам приведения
sin 2320 = cos 1420
cos 2320 = - sin 1420
z = 1 + cos 1420 - i sin 1420 = 2 cos 710(cos(-710) + i sin (-710))
Тригонометрическая форма:
z = 0,65 (cos(-710) + i sin (-710))
710 @ 1,24 рад.
Показательная форма:
z = 0,65 e1,24 i
Вычислим 1 + cos 1420 @ 0,211; sin 1420 @ 0,614
Алгебраическая форма:
z = 0,211 + 0,614i
5.2. Варианты заданий.
| № | Задания | № | Задания | |||||
1. z = -2 + 3i
2. а) z = 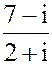 б) z = 3i171 - 2i123+ i10 - i
в) z =
б) z = 3i171 - 2i123+ i10 - i
в) z = 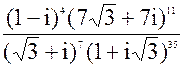 3. а) 2x2 - 6x + 13 = 0
б) x7 + 1 = 0
4. 5 + ixy = x + y + 4i
5. x1 = 2 + i
6. 1 + sin 120 + i cos 120
3. а) 2x2 - 6x + 13 = 0
б) x7 + 1 = 0
4. 5 + ixy = x + y + 4i
5. x1 = 2 + i
6. 1 + sin 120 + i cos 120
| 1. z = 3 -2i
2. а) z = 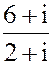 б) z = 3i151- 2i103+ i12 - i2
в) z =
б) z = 3i151- 2i103+ i12 - i2
в) z = 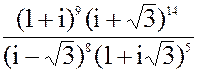 3. а) 2x2 + 4x - 11 = 0
б) x7 - 1 = 0
4. 3x -y + ixy = 3 + x + 2i
5. x1 = 1 + 2i
6. 1 + sin 180 + i cos 180
3. а) 2x2 + 4x - 11 = 0
б) x7 - 1 = 0
4. 3x -y + ixy = 3 + x + 2i
5. x1 = 1 + 2i
6. 1 + sin 180 + i cos 180
| |||||||
1. z = -5 + 2i
2. а) z = 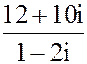 б) z = 3i147+ 2i130+ i26 - i21
в) z =
б) z = 3i147+ 2i130+ i26 - i21
в) z = 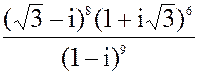 3. а) 3x2 + 4x + 12 = 0
б) 32x5 + 1 = 0
4. 7xy + 3i = 2x + y + 6xi
5. x1 = 1 -5i
6. 1 - sin 220 + i cos 220
3. а) 3x2 + 4x + 12 = 0
б) 32x5 + 1 = 0
4. 7xy + 3i = 2x + y + 6xi
5. x1 = 1 -5i
6. 1 - sin 220 + i cos 220
| 1. z = 11 + 7i
2. а) z = 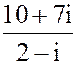 б) z = 3i137- 2i131- i2 + i1
в) z =
б) z = 3i137- 2i131- i2 + i1
в) z = 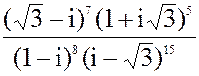 3. а) 2x2 + 2x + 17 = 0
б) 32x5 - 1 = 0
4.
3. а) 2x2 + 2x + 17 = 0
б) 32x5 - 1 = 0
4. 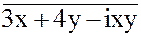 = 11 + 2i
5. x1 = 5 -i
6. 1 - sin 240 + i cos 240 = 11 + 2i
5. x1 = 5 -i
6. 1 - sin 240 + i cos 240
| |||||||
| № | Задания | № | Задания | |||||
1. z = -5 - 2i
2. а) z = 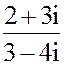 б) z = 6i144+ i117-3i13- 2i2
в) z =
б) z = 6i144+ i117-3i13- 2i2
в) z = 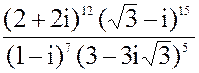 3. а) 3x2 + 10x + 15 = 0
б) 64x6 - 1 = 0
4. 3xy - 7i =
3. а) 3x2 + 10x + 15 = 0
б) 64x6 - 1 = 0
4. 3xy - 7i = 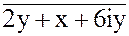 5. x1 = 3 + 2i
6. 1 + cos 220 - i sin 220
5. x1 = 3 + 2i
6. 1 + cos 220 - i sin 220
| 1. z = -7 -3i
2. а) z = 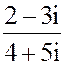 б) z = 6i124+ i97- 3i91 + 2i5
в) z =
б) z = 6i124+ i97- 3i91 + 2i5
в) z = 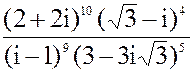 3. а) 5x2 + 4x + 1 = 0
б) 64x6 + 1 = 0
4. 3x -1 + iy =
3. а) 5x2 + 4x + 1 = 0
б) 64x6 + 1 = 0
4. 3x -1 + iy = 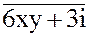 5. x1 = 2 + 5i
6. 1 + cos 240 + i sin 240
5. x1 = 2 + 5i
6. 1 + cos 240 + i sin 240
| |||||||
1. z = -3 + 5i
2. а) z = 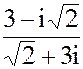 б) z = 5i913+ 2i96- 3i17+ 5i7
в) z =
б) z = 5i913+ 2i96- 3i17+ 5i7
в) z = 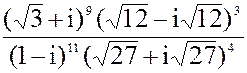 3. а) 2x2 + 4x + 11 = 0
б) x3 + 125 = 0
4. 2x + y + ixy =
3. а) 2x2 + 4x + 11 = 0
б) x3 + 125 = 0
4. 2x + y + ixy = 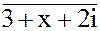 5. x1 = 2 -3i
6. 1 + sin 1160 + i cos 1160
5. x1 = 2 -3i
6. 1 + sin 1160 + i cos 1160
| 1. z = 3 + 5i
2. а) z = 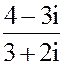 б) z = i1201- 5i403- 3i17 + i6
в)z =
б) z = i1201- 5i403- 3i17 + i6
в)z = 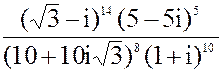 3. а) 2x2 - 13x + 100 = 0
б) x5 + 32 = 0
4. 11xy -2i =
3. а) 2x2 - 13x + 100 = 0
б) x5 + 32 = 0
4. 11xy -2i = 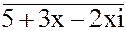 5. x1 = -3 +i
6. 1 + cos 200 - i sin 200
5. x1 = -3 +i
6. 1 + cos 200 - i sin 200
| |||||||
| № | Задания | № | Задания | |||||
1. z = -4 + 2i
2. а) z = 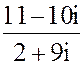 б) z = 2i153- 5i47+2i49- i18
в) z =
б) z = 2i153- 5i47+2i49- i18
в) z = 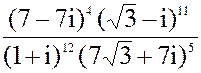 3. а) 3x2 + 4x + 13 = 0
б) x6 - 64 = 0
4. 3+x+y + 2i =
3. а) 3x2 + 4x + 13 = 0
б) x6 - 64 = 0
4. 3+x+y + 2i = 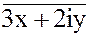 5. x1 = -3 + 5i
6. 1 + sin 220 + i cos 220
5. x1 = -3 + 5i
6. 1 + sin 220 + i cos 220
| 1. z = 8 - 4i
2. а) z = 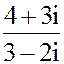 б) z = 2i63- 5i57+ 2i23- i10
в) z =
б) z = 2i63- 5i57+ 2i23- i10
в) z = 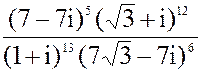 3. а) x2 - 8x + 21 = 0
б) x6 + 64 = 0
4. 5x + 2iy =
3. а) x2 - 8x + 21 = 0
б) x6 + 64 = 0
4. 5x + 2iy = 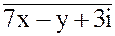 5. x1 = -3 - 5i
6. 1 + sin 240 + i cos 240
5. x1 = -3 - 5i
6. 1 + sin 240 + i cos 240
| |||||||
1. z = 7 + 14i
2. а) z = 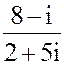 б) z = 5i713+ 2i316- 3i15+ 5i6
в) z =
б) z = 5i713+ 2i316- 3i15+ 5i6
в) z = 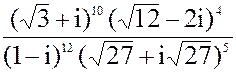 3. а) 2x2 - 8x + 13 = 0
б) x3 - 125 = 0
4. x + y + 4i =
3. а) 2x2 - 8x + 13 = 0
б) x3 - 125 = 0
4. x + y + 4i = 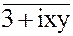 5. x1 = 2 +7i
6. 1 + sin 2020 + i cos 2020
5. x1 = 2 +7i
6. 1 + sin 2020 + i cos 2020
| 1. z = -1 - 4i
2. а) z =  б) z = 3i313-2i202+5i15+ i17
в)z =
б) z = 3i313-2i202+5i15+ i17
в)z = 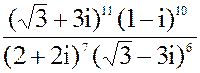 3. а) 2x2 + 4x + 15 = 0
б) 81x4 - 1 = 0
4. 3x +2iy =
3. а) 2x2 + 4x + 15 = 0
б) 81x4 - 1 = 0
4. 3x +2iy = 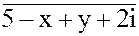 5. x1 = 7 +i
6. 1+ cos 1160 + i sin 1160
5. x1 = 7 +i
6. 1+ cos 1160 + i sin 1160
| |||||||
| № | Задания | № | Задания | |||||
1. z = -3 + 5i
2. а) z = 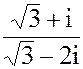 б) z = 5i114- 2i75+i36- i5
в) z =
б) z = 5i114- 2i75+i36- i5
в) z = 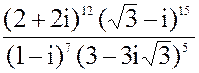 3. а) x2 - 13x + 100 = 0
б) x4 - 81 = 0
4. 6 + 2x + 2xi =
3. а) x2 - 13x + 100 = 0
б) x4 - 81 = 0
4. 6 + 2x + 2xi =  5. x1 = 3 + 5i
6. 1 + sin 980 - i cos 980
5. x1 = 3 + 5i
6. 1 + sin 980 - i cos 980
| 1. z = 2 -6i
2. а) z = 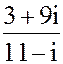 б) z = 5i134+ 2i79- i34- 2i7
в) z =
б) z = 5i134+ 2i79- i34- 2i7
в) z = 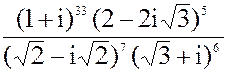 3. а) 2x2 + 8x + 15 = 0
б) x4 + 81 = 0
4. 9 + 7ixy =
3. а) 2x2 + 8x + 15 = 0
б) x4 + 81 = 0
4. 9 + 7ixy =  5. x1 = -3 + 2i
6. 1+ sin 1000 + i cos 1000
5. x1 = -3 + 2i
6. 1+ sin 1000 + i cos 1000
| |||||||
1. z = 7 + 3i
2/ а) z = 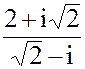 б) z = 3i197- 2i101+ 3i51+ i12
в) z =
б) z = 3i197- 2i101+ 3i51+ i12
в) z = 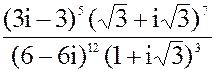 3. а) 6x2 + 4x + 1 = 0
б) 81x4 + 1 = 0
4. 6xy + 3i =
3. а) 6x2 + 4x + 1 = 0
б) 81x4 + 1 = 0
4. 6xy + 3i = 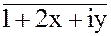 5. x1 = - 3 -5i
6. 1 - cos 160 - i sin 160
5. x1 = - 3 -5i
6. 1 - cos 160 - i sin 160
| 1. z = -2 - 3i
2. а) z = 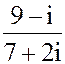 б) z = 3i187-2i91+ 3i33- i10
в)z =
б) z = 3i187-2i91+ 3i33- i10
в)z = 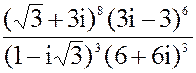 3. а) 3x2 + 8x + 15 = 0
б) x3 - 125 = 0
4.
3. а) 3x2 + 8x + 15 = 0
б) x3 - 125 = 0
4. 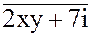 = 2y + x + 6yi
5. x1 = 3 +5i
6. 1 - cos 180 - i sin 180 = 2y + x + 6yi
5. x1 = 3 +5i
6. 1 - cos 180 - i sin 180
| |||||||
| № | Задания | № | Задания | |||||
1. z = 1 - 4i
2. а) z = 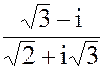 б) z = i571- 2i342+3i49- 2i14
в) z =
б) z = i571- 2i342+3i49- 2i14
в) z = 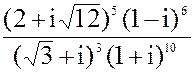 3. а) x2 + 2x + 17 = 0
б) x5 + 243 = 0
4. 3x + 2y + ixy =
3. а) x2 + 2x + 17 = 0
б) x5 + 243 = 0
4. 3x + 2y + ixy = 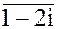 5. x1 = -2 - 3i
6. 1 + cos 160 + i sin 160
5. x1 = -2 - 3i
6. 1 + cos 160 + i sin 160
| 1. z = 11 + 22i
2. а) z = 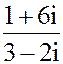 б) z = i197-2i142+3i79- 2i13
в) z =
б) z = i197-2i142+3i79- 2i13
в) z = 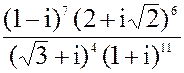 3. а) 3x2 + 6x + 13 = 0
б) 64x6 - 1 = 0
4. 5xy + 2i =
3. а) 3x2 + 6x + 13 = 0
б) 64x6 - 1 = 0
4. 5xy + 2i = 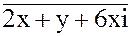 5. x1 = 12 + 5i
6. 1 + cos 200 + i sin 200
5. x1 = 12 + 5i
6. 1 + cos 200 + i sin 200
| |||||||
1. z = -3 - 5i
2. а) z = 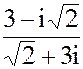 б) z = 5i917- 2i412- 3i17+ 5i11
в) z =
б) z = 5i917- 2i412- 3i17+ 5i11
в) z = 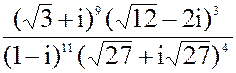 3.а) 2x2 + 4x + 11 = 0
б) 125x3 + 1 = 0
4.2x + y + ixy = 3 + x +2i
5.x1 = - 2 +3i
6. 1+ sin 1160 + i cos 1160
3.а) 2x2 + 4x + 11 = 0
б) 125x3 + 1 = 0
4.2x + y + ixy = 3 + x +2i
5.x1 = - 2 +3i
6. 1+ sin 1160 + i cos 1160
| 1.z = 7 - 14i
2.а) z = 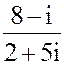 б) z = 5i717+2312- 3i15+5i6
в)z=
б) z = 5i717+2312- 3i15+5i6
в)z= 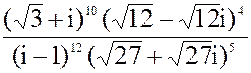 3.а) 2x2 + 8x + 13 = 0
б) 125x3 - 1 = 0
4.
3.а) 2x2 + 8x + 13 = 0
б) 125x3 - 1 = 0
4. 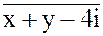 = 3 - ixy
5.x1 = 2 -7i
6. 1+ sin 2020 + i cos 2020 = 3 - ixy
5.x1 = 2 -7i
6. 1+ sin 2020 + i cos 2020
| |||||||
| № | Задания | № | Задания |
1. z = -2 - 3i
2. а) z = 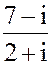 б) z = 3i171- 2i123+i23- i5
в) z =
б) z = 3i171- 2i123+i23- i5
в) z = 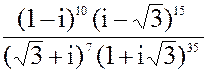 3. а) 2x2 - 6x + 13 = 0
б) x7 + 1 = 0
4. 5 + ixy = x +y +4i
5. x1 = 2 - i
6. 1+ sin 120 + i cos 120
3. а) 2x2 - 6x + 13 = 0
б) x7 + 1 = 0
4. 5 + ixy = x +y +4i
5. x1 = 2 - i
6. 1+ sin 120 + i cos 120
| 1. z = 3 + 2i
2. а) z = 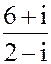 б) z = 3i157- 2i103+ i15- i10
в) z =
б) z = 3i157- 2i103+ i15- i10
в) z = 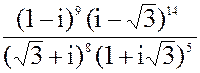 3. а) 2x2 + 4x + 11 = 0
б) x7 - 1 = 0
4. 3x -y+ ixy = 3 + x +2i
5. x1 = 1 + 2i
6. 1+ sin 240 + i cos 240
3. а) 2x2 + 4x + 11 = 0
б) x7 - 1 = 0
4. 3x -y+ ixy = 3 + x +2i
5. x1 = 1 + 2i
6. 1+ sin 240 + i cos 240
| ||
1. z = -5 - 2i
2. а) z = 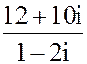 б) z = 3i147+ 2i131- i10+ i7
в) z =
б) z = 3i147+ 2i131- i10+ i7
в) z = 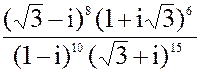 3.а) 3x2 + 4x + 12 = 0
б) 32x5 + 1 = 0
4. 7xy + 3i = 2x + y + 6xi
5. x1 = 1 +5i
6. 1 - sin 220 + i cos 220
3.а) 3x2 + 4x + 12 = 0
б) 32x5 + 1 = 0
4. 7xy + 3i = 2x + y + 6xi
5. x1 = 1 +5i
6. 1 - sin 220 + i cos 220
| 1. z = 11 + 7i
2. а) z = 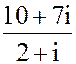 б) z = 3i137+2i123- i6+ i5
в)z =
б) z = 3i137+2i123- i6+ i5
в)z = 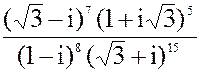 3. а) 2x2 + 2x + 17 = 0
б) x5 - 32 = 0
4.
3. а) 2x2 + 2x + 17 = 0
б) x5 - 32 = 0
4. 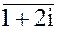 = 3x + 4y + ixy
5. x1 = 5 +i
6. 1 - sin 240 + i cos 240 = 3x + 4y + ixy
5. x1 = 5 +i
6. 1 - sin 240 + i cos 240
|
| № | Задания | № | Задания |
1. z = 5 + 2i
2. а) z = 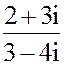 б) z = 6i144+ i117-3i13+ 2i10
в) z =
б) z = 6i144+ i117-3i13+ 2i10
в) z = 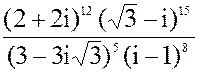 3. а) 3x2 + 10x + 15 = 0
б) x6 - 64 = 0
4. 3xy -7i = x +2y +6iy
5. x1 = 3 - 2i
6. 1+ cos 220 - i sin 220
3. а) 3x2 + 10x + 15 = 0
б) x6 - 64 = 0
4. 3xy -7i = x +2y +6iy
5. x1 = 3 - 2i
6. 1+ cos 220 - i sin 220
| 1. z = -7 + 3i
2. а) z = 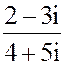 б) z = 6i124+ i97- 3i13+ 2i5
в) z =
б) z = 6i124+ i97- 3i13+ 2i5
в) z = 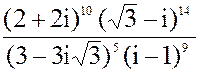 3. а) 5x2 + 4x + 1 = 0
б) x6 + 64 = 0
4. 3x -1+ iy = 6xy +3i
5. x1 = 2 - 5i
6. 1+ cos 240 - i sin 240
3. а) 5x2 + 4x + 1 = 0
б) x6 + 64 = 0
4. 3x -1+ iy = 6xy +3i
5. x1 = 2 - 5i
6. 1+ cos 240 - i sin 240
| ||
1. z = 3 + 5i
2. а) z = 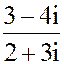 б) z = i1001- 5i507- 3i12- i8
в) z =
б) z = i1001- 5i507- 3i12- i8
в) z = 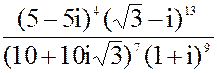 3.а) 2x2 - 10x + 15 = 0
б) 32x5 - 1 = 0
4. 1+3xy + ix = 9 + 7ixy
5. x1 = 1 +3i
6. 1 + cos 180 + i sin 180
3.а) 2x2 - 10x + 15 = 0
б) 32x5 - 1 = 0
4. 1+3xy + ix = 9 + 7ixy
5. x1 = 1 +3i
6. 1 + cos 180 + i sin 180
| 1. z = 3 + 6i
2. а) z = 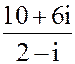 б) z = i138+3i127- i12+ 4i7
в)z =
б) z = i138+3i127- i12+ 4i7
в)z = 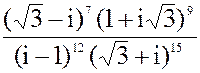 3. а) 2x2 - 2x + 17 = 0
б) x5 - 243 = 0
4.
3. а) 2x2 - 2x + 17 = 0
б) x5 - 243 = 0
4. 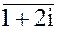 = 3x + 4y + ixy
5. x1 = 5 +2i
6. 1 - sin 250 + i cos 250 = 3x + 4y + ixy
5. x1 = 5 +2i
6. 1 - sin 250 + i cos 250
|
ЛИТЕРАТУРА
1. Пискунов Н.С. Дифференциальное и интегральное исчисление для ВТУЗов. Т. 1. – М: Наука, 1996.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М: Высшая школа, 1999.
3. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа,2007.
4. Киселев А.П. Алгебра. ч.2. – М: Физматлит, 2005
Date: 2015-07-02; view: 3671; Нарушение авторских прав