Множество действительных чисел как подмножество комплексных

Рассмотрим в С подмножество R_C чисел вида a +0 i, где a Î R: R_C ={ a +0 i | a Î R }. Так как

(a +0 i)+(b + ci)=(a + b)+(0+ ci)=(a + b)+ ci,

(a +0 i)(b + ci)=(ab -0× c)+(ac +0× b) i = ab + aci,

то, формально вынося в последнем равенстве за скобки множитель a, получаем (a +0 i)(b + ci)= a (b + ci) и в случае b + ci ¹0 _С, получаем a +0 i = a. Поэтому комплексное число a +0 i и действительное число a принято отождествлять: a +0 i = a. Таким образом, множество действительных чисел R считается подмножеством множества комплексных чисел С: R Í C. В частности, 0 _С =0, 1 _С =1 и в дальнейшем в обозначениях 0 _С и 1 _С индекс С будем опускать.

Кроме того, числа вида 0+ bi обозначают просто через bi. Наконец, в числах вида a +1 i единицу 1 не пишут: a +1 i = a + i.

Найдём, чему равен i ²: i ²=(0+ i)²=(0+ i)(0+ i)=(0-1)+(0+0) i =-1, то есть

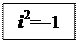
Таким образом, в частности, i ⁴= 1.

Наконец, рассматривая число a + bi как сумму (a +0 i)+(0+ bi), его можно возводить в произвольную натуральную степень n по формуле бинома Ньютона:

(a + bi) ⁿ = ,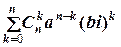

в частности,

(a + bi)²= a ²+2 abi +(bi)²= a ²+2 abi - b ²=(a ²- b ²)+2 abi,

(a - bi)²= a ²-2 abi +(bi)²= a ²-2 abi - b ²=(a ²- b ²)-2 abi,

(a + bi)³= a ³+3 a ²(bi)+3 a (bi)²+(bi)³= a ³+3 a ² bi -3 ab ²- b ³ i =(a ³-3 ab ²)+(3 a ² b - b ³) i,

(a + bi)³=(a ³-3 ab ²)-(3 a ² b + b ³) i.

Например, при решении упражнения 1.1.4. г) и можно найти по этим формулам:

(2+ i)³=2³+3×2² i +3×2 i ²+ i ³=8+12 i -6- i =2+11 i,

(2- i)³=2³-3×2² i +3×2 i ²- i ³=8-12 i -6+ i =2-11 i.

1.2.2. Упражнение. Вычислить:

а) i ⁵⁵; б) i 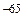; в) i ⁸⁸; г) iⁿ; д) (1+ i)^{8 n} ; е) (1+ i)^{4 n} ; ж) (1- i)^{8 n} ; з) (1- i)^{4 n} , n Î Z.

Решение. б) По свойствам степени с целым показателем имеем i 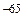=(i ⁶⁵) 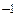. Найдём отдельно i ⁶⁵. Так как 65=4×16+1, то

i ⁶⁵= i ^4×16+1 =(i ⁴)¹⁶× i =1× i = i.

Поэтому

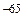i 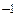= i = i 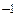× i ⁴ = i ³ = - i.

д) Имеем

(1+ i)²= 1²+2 i + i ²=1+2 i -1=2 i.

Поэтому

(1+ i)^{8 n} =((1+ i)²)^{4 n} =(2 i)^{4 n} =((2 i)⁴) ⁿ =(2⁴ i ⁴) ⁿ =16 ⁿ.

Date: 2015-07-02; view: 691; Нарушение авторских прав