
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Корни из комплексного числа и их вычисление
|
|
2.5.1. Определение. Пусть n ¾ натуральное число. Корнем n - й степени из комплексного числа a называется такое комплексное число b, что 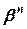 = a.
= a.
Корень n -й степени из комплексного числа a обозначается через 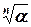 .
.
2.5.2. Теорема. Существует в точности n различных значений корня n - й степени из комплексного числа a. Они вычисляются по формуле
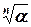 =
= 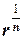 (cos
(cos 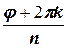 + i sin
+ i sin 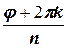 ), (2.5.1)
), (2.5.1)
где r ¾ модуль числа a, j ¾ его аргумент, l ¾ произвольное целое число, k пробегает все значения от 0 до n -1.
Таким образом, множество значений корня n -й степени ¾ следующее
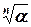 =
= 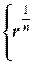 (cos
(cos 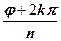 + i sin
+ i sin 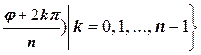 . (2.5.2)
. (2.5.2)
2.5.3. Упражнение. Вычислить:
а) 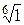 ; б)
; б) 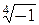 ; в)
; в) 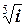 ; г)
; г) 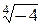 ; д)
; д) 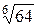 ; е)
; е) 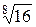 ;
;
ж)  ; з)
; з) 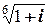 .
.
Решение. б) Найдём тригонометрическую форму числа -1: -1= =cos p + i sin p. Тогда по (2.5.2) имеем
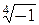 ={ wk =cos
={ wk =cos 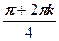 + i sin
+ i sin 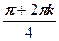 | k =0, 1, 2, 3}.
| k =0, 1, 2, 3}.
Найдём каждое значение wk в отдельности:
w 0 = cos 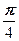 + i sin
+ i sin 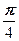 =
= 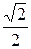 +
+ 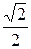 i;
i;
w 1 = cos 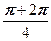 + i sin
+ i sin 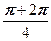 =cos
=cos 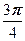 + i sin
+ i sin 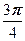 = -
= - 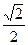 +
+ 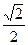 i;
i;
w 2 = cos 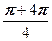 + i sin
+ i sin 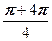 =cos
=cos 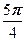 + i sin
+ i sin 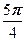 = -
= - 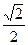 -
- 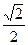 i;
i;
w 3 = cos 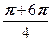 + i sin
+ i sin 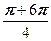 =cos
=cos 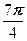 + i sin
+ i sin 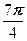 =
= 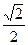 -
- 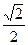 i;
i;
Ответ: б) 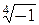 ={
={ 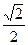 +
+ 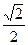 i, -
i, - 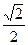 +
+ 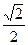 i, -
i, - 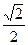 -
- 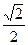 i,
i, 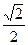 -
- 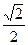 i }.
i }.
2.5.4. Вычисление квадратного корня из комплексного числа в большинстве случаев удобно производить по следующей схеме. Пусть требуется найти 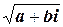 . Будем искать
. Будем искать 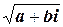 в виде x + yi:
в виде x + yi:
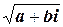 = x + yi. (2.5.3).
= x + yi. (2.5.3).
Возведём обе части (2.5.3) в квадрат: a + bi =(x 2- y 2)+2 xyi. Теперь, приравняв в обеих частях действительные и мнимые части, приходим к системе
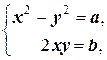
решая которую, находим x и y.
Например, пусть требуется найти 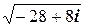 . Положим
. Положим 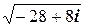 = = x + yi, откуда получаем -28+8 i =(x 2- y 2)+2 xyi и приходим к системе
= = x + yi, откуда получаем -28+8 i =(x 2- y 2)+2 xyi и приходим к системе
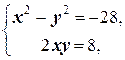
Выражая из второго уравнения y через x (y = 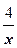 ) и подставляя его в первое, приходим к уравнению x 2-
) и подставляя его в первое, приходим к уравнению x 2- 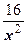 =-28, которое приводится к виду x 4+28 x 2-16=0. Оно - биквадратное. Положим t = x 2 и решим полученное квадратное уравнение t 2+28 t -16=0. Получаем решения: t 1=-14+2
=-28, которое приводится к виду x 4+28 x 2-16=0. Оно - биквадратное. Положим t = x 2 и решим полученное квадратное уравнение t 2+28 t -16=0. Получаем решения: t 1=-14+2 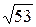 и t 1=-14-2
и t 1=-14-2 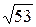 . Второе отбрасываем из рассмотрения, так как x =
. Второе отбрасываем из рассмотрения, так как x =  должен быть действительным. Поэтому x 1,2=
должен быть действительным. Поэтому x 1,2= 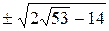 . Отсюда y 1,2=
. Отсюда y 1,2= 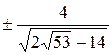 , то есть
, то есть
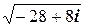 ={
={ 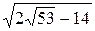 +
+ 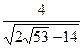 i, -
i, - 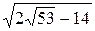 -
- 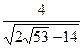 i }.
i }.
2.5.5. Упражнение. Вычислить 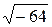 ,
, 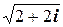 ,
, 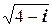 ,
, 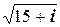 .
.
2.5.6. Можно показать, что квадратное уравнение ax 2+ bx + c =0, где a, b, c Î C, имеет корни 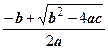 .
.
2.5.7. Упражнение. Решить уравнения:
а) x 2-1=0; б) x 2+2=0; в) x 2-2- i =0; г) x 2+2 x +2=0;
д) x 2+(2+ i) x +(3-2 i)=0; е) 4 x 2-(2- i) x +(6-2 i)=0.
Решение. д) Корнями являются числа
x 1,2= 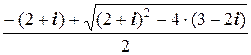 .
.
Найдём отдельно выражение под корнем:
(2+ i)2-4×(3-2 i)=4+4 i -1-12+8 i =-8+12 i.
Поэтому 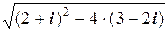 =
= 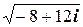 . Этот корень будем искать по правилу, изложенному в 2.5.4:
. Этот корень будем искать по правилу, изложенному в 2.5.4:
-8+12 i =(x 2- y 2)+2 xyi, откуда 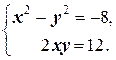 Далее, опуская комментарии, имеем y =
Далее, опуская комментарии, имеем y = 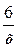 , x 2-
, x 2- 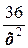 =-8, x 4+8 x 2-36=0, t = x 2, t 2+8 t -36=0, D =82-4×(-36)=208=16×13, t =2
=-8, x 4+8 x 2-36=0, t = x 2, t 2+8 t -36=0, D =82-4×(-36)=208=16×13, t =2 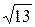 -4, t 1, 2=
-4, t 1, 2= 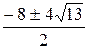 =-4±2
=-4±2 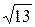 , x =±
, x =± 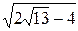 , y =±
, y =± 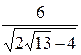 ,
, 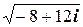 =±(
=±(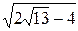 +
+ 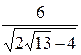 i). Теперь
i). Теперь
x 1,2= 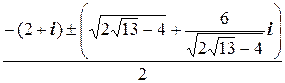 =
=  =
=
= 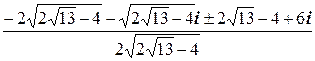 =
=
= 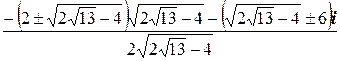 .
.
Ответ. x 1= 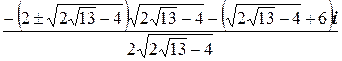 ,
,
x 2= 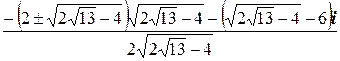 .
.
[1] Понятие «множество», другие понятия и обозначения,связанные с ним, см. Приложение 3.
[2] Ниже в угловых скобках мелким шрифтом приводятся комментарии к преобразованиям
Date: 2015-07-02; view: 888; Нарушение авторских прав