
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Геометрическое изображение комплексных чисел
|
|
Поскольку комплексное число z = x + iy можно интерпретировать как упорядоченную пару чисел (x,y), то удобно изображать комплексное число как точку на плоскости с этими координатами. Саму плоскость при этом называют комплексной плоскостью.
Длина r радиус-вектора OM (рис.1) называется модулем комплексного числа и обозначается |z|, а угол j, образованный радиус-вектором с осью Ох и отсчитываемый против часовой стрелки, - аргументом комплексного числа; он обозначается через Аrg z.
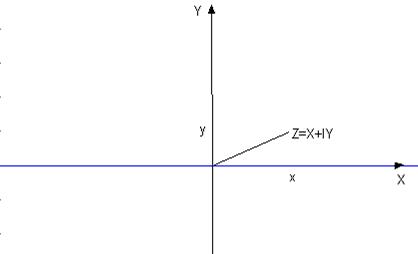
Рис. 1
Очевидно, аргумент комплексного числа определяется неоднозначно, а с точностью до слагаемого, кратного 2p:
j = arg z + 2kp, k = 0, ±1, ±2,...,
где 0£ arg z£2p – главное значение аргумента.
Из чертежа видно, что
r = |z| = 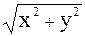 (3); tg j =
(3); tg j = 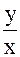 (4).
(4).
Так как формула (4) не определяет угол j однозначно, то следует учитывать следующие соотношения:
arg z = arctg 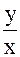 при x > 0, y ³ 0;
при x > 0, y ³ 0;
arg z = p + arctg 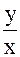 при x < 0, y ³ 0;
при x < 0, y ³ 0;
arg z = p + arctg 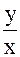 при x < 0, y < 0;
при x < 0, y < 0;
arg z = 2p + arctg 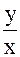 при x > 0, y < 0.
при x > 0, y < 0.
Примеры.
Изобразить на комплексной плоскости числа
1) z1 = 1+i; 2) z2 = - 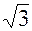 +i; 3) z3 = -1-i; 4) z4 = 1-i
+i; 3) z3 = -1-i; 4) z4 = 1-i 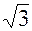 ;
;
5) z5 = -1; 6) z6 = -2i
и найти их модули и аргументы.
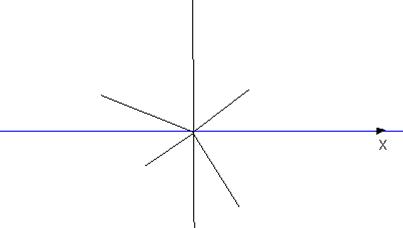
Рис. 2
Решение.
При решении всех примеров выбиралось главное значение аргумента.
1) 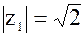 , tg , tg 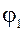 =1, =1, 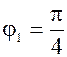
| 4) 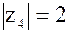 , tg , tg 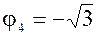 , , 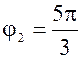
|
2) 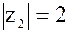 , tg , tg  , , 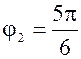
| 5) 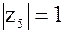 , tg , tg 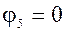 , , 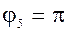
|
3) 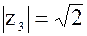 , tg , tg 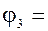 1, 1, 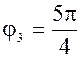
| 6) 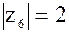 , tg , tg 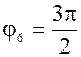
|
Date: 2015-07-02; view: 690; Нарушение авторских прав