
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Понятие комплексного числа. Операции над комплексными числами
|
|
Глава 1. Комплексные числа
Комплексные числа.
Понятие комплексного числа. Операции над комплексными числами.
1.1.1. Определение. Комплексным числом называется выражение вида a + bi, где a и b ¾ произвольные действительные числа, i ¾ некоторый новый символ, называемый мнимой единицей; a называется действительной частью, b ¾ мнимой частью комплексного числа a + bi.
Множество всех комплексных чисел обозначается через С: С ={ a + bi | a, b Î R }[1].
Действительная часть a комплексного числа a = a + bi обозначается через Re a, а мнимая часть ¾ через Im a. Таким образом, если a = a + bi, то Re a = a и Im a = b.
Два комплексных числа называются равными, если их действительная и мнимая части равны соответственно: a = b Û Re a =Re b и Im a =Im b.
Число a +(- b) i обозначают через a - bi, то есть a +(- b) i = a - bi.
1.1.2. Определение. Суммой двух комплексных чисел a + bi и c + di называется комплексное число (a + c)+(b + d) i. Их произведением называется комплексное число (ac - bd)+(ad + bc) i.
Сумма комплексных чисел a и b обозначается через a + b, а их произведение ¾ через ab. Таким образом, по определению
(a + bi)+(c + di)=(a + c)+(b + d) i и (a + bi)(c + di)=(ac - bd)+(ad + bc) i.
1.1.3. Теорема. Операции сложения и умножения над комплексными числами удовлетворяет условиям:
1) Для любых a, b из С следует, что a + b = b + a.
2) Для любых a, b и g из С следует, что (a + b)+ g = a +(b + g).
3) Для любых a, b и g из С следует, что
(a + b) g = ag + bg и a (b + g)= ab + ag.
4) В С существуют такие комплексные числа 0 С и 1 С, что 0 С + a = a +0 С = a и 1 С × a = a ×1 С = a для любого a из С.
5) Для любого a из С в С существует b такой, что a + b =0 С. Такой b обозначается через - a.
6) Для любого a ¹0 С из С в С существует b такой, что a × b =1 С.
При этом 0 С =0+0 i, 1 С =1+0 i, если a = a + bi, то - a =(- a)+(- b) i, и если a = a + bi ¹0 С (то есть a 2+ b 2¹0), то a 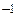 =
= 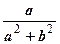 -
- 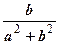 i. Числа 0 С и 1 С называются соответственно комплексным нулём и комплекснойединицей, - a - противоположным кa, a
i. Числа 0 С и 1 С называются соответственно комплексным нулём и комплекснойединицей, - a - противоположным кa, a 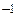 - обратным кa.
- обратным кa.
Как видим, свойства 1) - 6) операций сложения и умножения над комплексными числами практически идентичны аналогичным операциям над действительными числами. Из этих свойств (назовём их основными) вытекают другие, которые также идентичны свойствам сложения и умножения действительных чисел. Среди них укажем следующие:
7) 0 С и 1 С единственны.
8) В суммах и произведениях вида (…((a 1+ a 2)+ a 3)+…+ ak) и (…((a 1 a 2) a 3)… ak) скобки можно расставлять произвольным образом. В связи с этим скобки принято опускать:
(…((a 1+ a 2)+ a 3)+…+ a k)= a 1+ a 2+…+ ak,
(…((a 1 a 2) a 3)… ak)= a 1 a 2… ak.
9) Для любого a из С -(- a)= a и (a 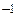 )
) 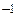 = a (a ¹0 С).
= a (a ¹0 С).
10) Для любых a, b из С существует единственное х из С такое, что х + a = b и a + х = b. Оно равно х = b +(- a). Это число обозначается через b - a и называется разностью чисел b и a.
11) Для любых a, b из С (a ¹0 С) существует единственное х из С такое, что х a = b и a х = b. Оно равно х = ba 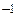 . Это число обозначается через
. Это число обозначается через  и называется частным чисел b и a.
и называется частным чисел b и a.
12) Для любых комплексных чисел a 1, a 2, …, ak, b имеют место равенства
(a 1± a 2±…± ak) b = a 1 b ± a 2 b ±…± akb,
b (a 1± a 2±…± ak)= ba 1± ba 2±…± bak.
Наконец, для комплексных чисел, так же, как и для действительных, определена степень с целым показателемk:
ak = 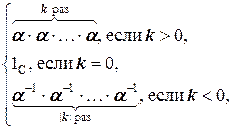
для которой выполнены свойства, аналогичные свойствам степени действительного числа с целым показателем:
akal = ak + l , 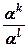 = ak - l, (ak) l = akl, akb k =(ab) k,
= ak - l, (ak) l = akl, akb k =(ab) k, 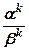 =
= 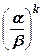 .
.
Отметим также, что справедливы свойства, аналогичные для степеней сумм и разностей действительных чисел. В частности, для любых комплексных чисел a и b имеют место формулы сокращённого умножения:
a 2 - b 2=(a - b)(a + b),
a 3 - b 3=(a - b)(a 2 + ab + b 2),
a 3 + b 3=(a + b)(a 2 - ab + b 2),
(a + b)2= a 2 +2 ab + b 2,
(a - b)2= a 2 -2 ab + b 2,
(a + b)3= a 3 +3 a 2 b +3 ab 2+ b 3,
(a - b)3= a 3 -3 a 2 b +3 ab 2- b 3.
В общем случае справедлива формула бинома Ньютона:
(a + b) n = 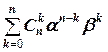 .
.
1.1.4. Упражнение. Вычислить:
а) (3-2 i)(2+3 i)+(5+2 i)(2- i); г) 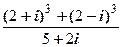 ;
;
б) (3-2 i)(1-3 i)-(5+2 i)(1+2 i); д) 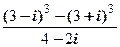 ;
;
в) 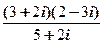 ; е)
; е) 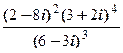 .
.
Решение. г) Найдём отдельно числитель, предварительно вычислив (2+ i)3 и (2- i)3.
Имеем
(2+ i)2=(2+ i)(2+ i)=(2×2-1×1)+(2×1+1×2) i =3+4 i,
(2+ i)3=(2+ i)2(2+ i)=(3+4 i)(2+ i)=(3×2-4×1)+(3×1+4×2) i =2+11 i,
(2- i)2=(2+(-1) i)2=(2+(-1) i)(2+(-1) i)=(2×2-(-1)×(-1))+(2×(-1)+(-1)×2) i =3-4 i,
(2- i)3=(2- i)2(2- i)=(3-4 i)(2- i)=(3×2-(-4)×(-1))+(3×(-1)+(-4)×2) i =2-11 i.
Поэтому
(2+ i)3+(2- i)3 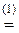 [2][(2+ i)+(2- i)][(2+ i)2-(2+ i)(2- i)+(2- i)2]=
[2][(2+ i)+(2- i)][(2+ i)2-(2+ i)(2- i)+(2- i)2]=
=(4+0 i)[(3+4 i)-(5+0 i)+(3-4 i)]=(4+0 i)(1+0 i)=4+0 i.
Далее,
(2+ i)3+(2- i)3=(2+11 i)+(2-11 i)=(2+2)+(11+(-11)) i =4+0 i,
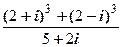 =
= 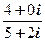 =(4+0 i)(5+2 i)
=(4+0 i)(5+2 i) 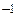 =(4+0 i)(
=(4+0 i)(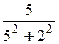 +
+ 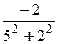 i)=
i)=
=(4+0 i)(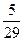 -
- 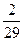 i)=[4×
i)=[4× 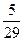 -0×(-
-0×(- 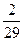 )]+[4×(-
)]+[4×(- 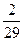 )-0×
)-0× 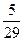 ] i =
] i = 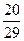 -
- 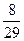 i.
i.
á(1) применяем формулу для a 3+ b 3 при a =2+ i и b =2- i ñ
Ответ: 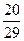 -
- 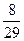 i.
i.
Date: 2015-07-02; view: 810; Нарушение авторских прав