Действия над комплексными числами. Кафедра математики и информатики

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КИНО И ТЕЛЕВИДЕНИЯ»

Кафедра математики и информатики

КОМПЛЕКСНЫЕ ЧИСЛА

Методические указания

к выполнению расчетно-графической работы

Для студентов ФАВТ, ФПСКТ, ФФиТРМ

Санкт-Петербург

Составитель: старший преподаватель Е.Ю. Непомнящая

Рецензент: заведующий кафедрой математики и информатики СПбГУКиТ, доктор физ-мат. наук, профессор И.Н.Щитов

Рекомендовано к изданию в качестве методических указаний кафедрой математики и информатики.

Протокол № 11 от 11.04.2011 г.

Комплексные числа.

Действия над комплексными числами.

Комплексным числом z называется выражение вида

z = x + iy, где х и у -вещественные числа, а i = так называемая мнимая единица, определяемая условием i² = - 1.

Число х называется вещественной частью комплексного числа z и обозначается Rez, а у - мнимой частью z и обозначается Im z.

Два комплексных числа z₁ = x₁ + i y₁ и z₂ = x₂ + i y₂ равны тогда и только тогда, когда равны их вещественные и мнимые части:

z₁ = z₂ Û x₁ = x₂; y₁ = y₂

Сумма и разность комплексных чисел

z₁ = x₁ + i y₁ и z₂ = x₂ + i y₂

определяются соответственно равенствами

z₁ ± z₂ = x₁ ± x₂+ i (y₁ ± y₂) (1)

Произведение комплексных чисел z₁ и z₂ определяется равенством

z₁z₂ = x₁x₂ - y₁y₂ + i(x₁y₂ + x₁y₂) (2)

Комплексное число вида z = x + i∙0 можно отождествить с вещественным числом x. Таким образом, вещественное число является частным случаем комплексного числа, когда его мнимая часть равна нулю.

Запись комплексного числа в виде z = x + iy называется алгебраической формой комплексного числа.

Нетрудно видеть, что действия сложения, вычитания и умножения с комплексными числами в алгебраической форме производятся так же, как с алгебраическими двучленами, при этом следует учитывать, что i² = - 1.

Число`z называется комплексно сопряженным с числом

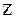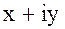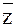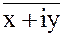= : = = x - iy

Чтобы найти частное от деления двух комплексных чисел, нужно умножить и числитель, и знаменатель дроби на число, сопряженное знаменателю:

= = =

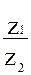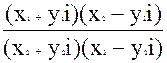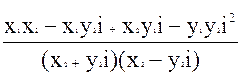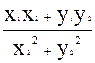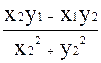= + i

Примеры.

Даны два комплексных числа:

z₁=3-2i; z₂=-1+4i

Найти: 1) z₁+z₂; 2) z₁-z₂; 3) z₁×z₂; 4) 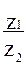; 5) ; 6)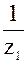

Решение.

1) z₁+z₂ = (3-2i)+(-1+4i) = 2+2i;

2) z₁-z₂ = (3-2i) -(-1+4i) = 4-6i;

3) z₁×z₂ = (3-2i)×(-1+4i) = -3+12i+2i-8i² = -3+8+14i = 5+14i;

4) = = = =

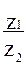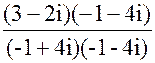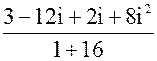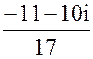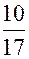= - - i;

5) = =

= = = - + i;

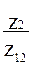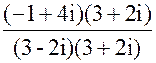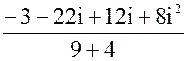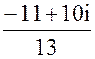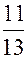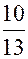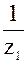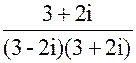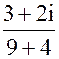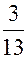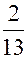6) = = = = + i

Date: 2015-07-02; view: 481; Нарушение авторских прав