Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Формы представления комплексных чисел
|
|
Комплексные числа
Определение комплексного числа.
Число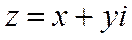 
(1.1),
где 
- действительные числа, 
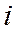- мнимая единица, называется комплексным числом.
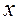называется вещественной частью комплексного числа, 
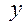- мнимой частью.
Выражение 
(1.2)
называется мнимой единицей.
Графически комплексное число изображается точкой на комплексной плоскости или радиус-вектором этой точки. Ось абсцисс называется вещественной осью, ось ординат – мнимой осью. (Рис. 1.1)
Рассмотрим значения степеней мнимой единицы
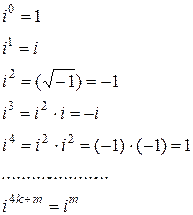(1.3)
Формы представления комплексных чисел
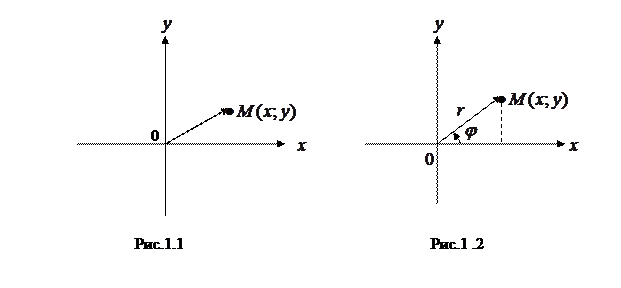
Форма 
называется алгебраической формой комплексного числа.
Комплексное число может быть представлено в тригонометрической форме. Из рисунка 1.2 следует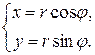 
Подставив эти значения в уравнение (1.1), получаем
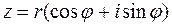(1.4)
- тригонометрическая форма комплексного числа.
Известна формула Эйлера, связывающая показательную функцию комплексного переменного с тригонометрическими функциями вещественного переменного:
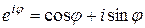. Учитывая эту формулу, формулу (1.4) можно переписать в виде: 
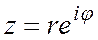(1.5) - показательная форма комплексного числа.
Замечание. В показательной и тригонометрической формах комплексного числа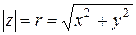 
- модуль комплексного числа,
Аргументом комплексного числа называется угол между положительным направлением вещественной оси и радиус-вектором числа. Эта координата многозначна.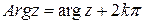 
. 
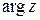называется главным значением аргумента, который 
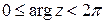или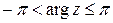 
.
Пример 1. Записать число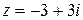 
в тригонометрической форме.
Находим модуль числа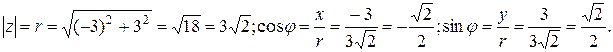 
Поскольку 
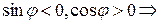число находится во второй четверти, 
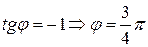. Окончательно, 
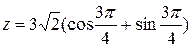- тригонометрическая форма числа. 
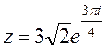- показательная форма заданного комплексного числа.
Если x =0, комплексное число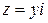 
называется чисто мнимым, оно находится на мнимой оси, если y =0, число 
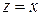- действительное.
Число 
называется сопряженным числу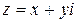 
.
Число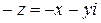 
называется противоположным числу 
.
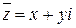Date: 2015-07-02; view: 935; Нарушение авторских прав