
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Порядок выполнения работы
|
|
а) Получить явную формулу для моделирования случайной величины с законом распределения, заданным в таблице 4. Если необходимо, найти неизвестные параметры.
б) Моделирование случайной величины X = {xi} = x1, x2, …, xn выполнить с помощью последовательности чисел R = {ri} = r1, r2, …, rn, полученных указанным в таблице 4 способом построения случайных чисел.
в) Вычислить критерий χ2 Пирсона при k=16 или k=21 для последовательности случайных чисел X = {xi} = x1, x2, …, xn и сделать заключение о соответствии смоделированной величины данному закону распределения.
г) Вывести на экран заполненную интервальным статистическим рядом таблицу (см. таблицу 3); гистограмму, построенную по таблице 3; теоретический и практический графики случайных величин, моделируемых по заданному закону распределения; значение критерия χ2 Пирсона.
Таблица 4 – Варианты заданий
| Вариант | Закон распределения | Способ построения |
| Экспоненциальный, λ=2 | Метод обратных функций, формула (2) | |
| Нормальный, N(0;1) | Метод отбора | |
| Экспоненциальный, λ=3 | Метод отбора | |
| Распределение Пуассона, формула (15); λ=9 | Алгоритм - формула (17) | |
| Нормальный, (0; 0.81), формула (18) | Метод отбора | |
| Нормальный, N(0; 1) | Аппроксимация распределения; формула (19) | |
| Гамма-распределение; формула (25); λ=3 | Формула (26) | |
Логарифмическо-нормальный,
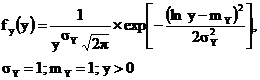
| Метод отбора | |
Закон Вейбулла,
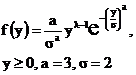
| Метод отбора | |
| Бета-распределение, формула (22); m=2, p=1.5 | Формула (23) | |
| Нормальный, N(0; 1) | Аппроксимация; формула (3) |
Продолжение таблицы 4
| Бета-распределение, формула (22); m=5, p=2.3 | Метод Йонка | |
| Дискретное распределение; k=10; p1=0.5; p5=0.04; p8=0.95; p2=0.8; p6=0.09; p9=0.97; p3=0.7; p7=0.3; p10=0.35. p4=0.2; | Формула (5) | |
| Усеченное нормальное распределение, формула (8) | Процедура 4 | |
| Распределение Вейбулла (см. вариант 9); a=2.5; σ=2; g1(x)=xa-1 | Процедура 3 | |
| Нормальный, N(0; 1) | Комбинация метода суперпозиции и метода отбора, (12) | |
| Биномиальный, формула (13); p=0.3 | См. п. 5.1 | |
| Закон Вейбулла (см. вариант 9); a=2; σ=3 | Процедура 2 | |
Закон Релея:
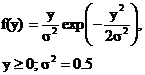
| Процедура 1 | |
| Экспоненциальный; λ=0.4 | Метод обратных функций, формула (2) | |
| Нормальный; N(0; 1) | Процедура Марсальи и Брея, формула (21) | |
| Дискретное распределение; k=12; p1=0.3; p5=0.39; p9=0.9; p2=0.2; p6=0.8; p10=0.3; p3=0.4; p7=0.89; p11=0.05; p4=0.38; p8=0.7; p12=0.03. | Формула (5) | |
| Гамма-распределение; формула (25); λ=4 | Формула (26) | |
| Нормальный, N(2, 1) | Аппроксимация распределения; формула (19) |
Содержание отчета
1. Титульный лист.
2. Постановка задачи (вариант, задание).
3. Ход работы:
- Математическая модель (вывод формулы для моделирования заданной случайной величины).
- Полученные результаты (таблицы, графики).
- Описание листинга программы.
4. Отчет распечатать.
[1] Кнут Д.Э. Искусство программирования. Т.2.: Получисленные алгоритмы / Под общ. ред. Козаченко Ю.В. - 3-е изд. - М.: Вильямс, 2001. - 828с. - Предм.-имен. указ.:с. 801-828. [с. 157]
Date: 2015-07-17; view: 1221; Нарушение авторских прав