Распределение Пуассона

Пуассоновское распределение – это распределение случайной величины, которая равна числу событий, происшедших в единицу времени.

Случайная величина X имеет распределение Пуассона, если

(15)

где λ - параметр распределения.

Моделирующий алгоритм основывается на следующем утверждении: если случайные величины X₁, X₂, … независимы и все имеют экспоненциальное распределение с математическим ожиданием, равным 1, то неотрицательное целое число n, для которого выполняется неравенство

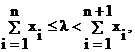(16)

имеет распределение Пуассона с параметром λ.

В связи с тем, что X_i = -ln r_i, где r_i - случайная величина R с равномерным распределением на [0;1), условие (16) можно записать в виде

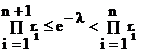, (17)

где 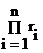– произведение всех r_i, таких, что значение i – целое и выполняется соотношение i=1…n.

На основании (17) можно построить алгоритм получения случайной величины, распределенной по закону Пуассона (15) с параметром λ:

а) реализуются последовательности r₁, r₂, …, r_n независимых случайных величин, равномерно распределенных на [0; 1);

б) вычисляются произведения r₁, r₁r₂, r₁r₂r₃, … до тех пор, пока не выполнится условие

.

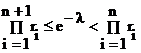В качестве значения случайной величины X принимается число n. Если неравенству удовлетворяет первое из равномерно распределенных чисел r₁, то X=0.

Моделирование случайных чисел X, имеющих закон распределения Пуассона (15), может быть реализовано другими способами. С этой целью можно воспользоваться предельной теоремой Пуассона, в соответствии с которой, если p – вероятность наступления события A при одном испытании, то вероятность наступления m событий в N независимых испытаниях при N→∞, p→0, N_p=λ асимптотически равна p(X=m).

Выберем достаточно большое N, такое, чтобы p=λ/N<1, и будем проводить серии по N независимых испытаний, в каждом из которых событие A происходит с вероятностью p, и будем подсчитывать число случаев y_j фактического наступления события A в серии с номером j. Числа y_j будут приближенно следовать закону Пуассона, причем тем точнее, чем больше N. Практически N должно выбираться таким образом, чтобы p=0.1 + 0.2.

Date: 2015-07-17; view: 1067; Нарушение авторских прав