
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Выборка. Эмпирическая функция распределения. Гистограмма
|
|
В математической статистике имеют дело со стохастическими экспериментами, состоящими в проведении n повторных независимых наблюдений над некоторой случайной величиной X ={xi}=x1, x2, xn, имеющей неизвестное распределение вероятностей, т.е. неизвестную функцию распределения Fx (х) = F (х).
В этом случае множество X возможных значений наблюдаемой случайной величины Х называют генеральной совокупностью, имеющей функцию распределения F (х).
Числа х1,,…,xn, xi Î X, i = 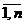 , являющиеся результатом n независимых наблюдений над случайной величиной X, называют выборкой из генеральной совокупности или выборочными (статистическими) данными. Число n называется объемом выборки.
, являющиеся результатом n независимых наблюдений над случайной величиной X, называют выборкой из генеральной совокупности или выборочными (статистическими) данными. Число n называется объемом выборки.
В таблице 1 приведены обозначения параметров выборки для выборочных значений.
Таблица 1 – Параметры выборки
| Параметр | Обозначение | Определение |
| Выборочные данные | xi, где i = 1,... n | Наблюденные значения случайной величины |
| Объем выборки | n | Количество случайных чисел в выборке |
Выборка является исходной информацией для статистического анализа и принятия решений о неизвестных вероятностных характеристиках наблюдаемой случайной величины X. Однако на основе конкретной выборки обосновать качество статистических выводов невозможно. Для этих целей на выборку следует смотреть априори как на случайный вектор (Х 1, …, Xn), координаты которого являются независимыми, распределенными так же как и X, случайными величинами, и который еще не принял конкретного значения в результате эксперимента. Существует несколько способов представления статистических данных. Простейший из них – в виде статистического ряда:
| Номер наблюдения i | 1 2 … n |
| Результат наблюдения xi | x1 x2 … xn |
Если среди выборочных значений имеются совпадающие, то статистический ряд удобнее записывать в виде следующей таблицы 2.
Таблица 2 – Статистический ряд
| Выборочные значения yi | y1 | y2 | … | yr |
| Частоты mi | m1 | m2 | … | mr |
| Относительные частоты pi* = mi/n | m1/n | m2/n | … | mr/n |
Здесь (у1, …,yr) (r < n) – различные значения среди х1, …,xn; mi –частота значения уi, pi *= mi / n - относительная частота значения yi. Очевидно, что
 .
.
Совокупность пар 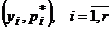 называют иногда эмпирическим законом распределения, а саму таблицу 2 – таблицей частот. Выборочные значения х1, …,xn, упорядоченные по возрастанию, носят название вариационного ряда:
называют иногда эмпирическим законом распределения, а саму таблицу 2 – таблицей частот. Выборочные значения х1, …,xn, упорядоченные по возрастанию, носят название вариационного ряда:
x(1 ) £ x(2)£…£ x(n),
где x (1) =min{ x1,…,xn }, x ( n ) =max{ x1,…,xn }.
Величина  называется размахом выборки.
называется размахом выборки.
Эмпирической функцией распределения, соответствующей выборке х1, …, xn, называется функция
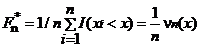 ,
,
где I (A)–индикатор множества A, а 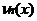 – число выборочных значений, не превосходящих x. Для каждой выборки х1, …, xn функция Fn *(х) является неубывающей и непрерывной слева. Ее график имеет ступенчатый вид:
– число выборочных значений, не превосходящих x. Для каждой выборки х1, …, xn функция Fn *(х) является неубывающей и непрерывной слева. Ее график имеет ступенчатый вид:
- если все значения х1, …, xn различны, то Fn *(х)= i/n при x Î[ x ( i ), x ( i+1 )), x (0) =- ¥, x ( n+1 ) = ¥;
- если y1, …,yr –различные значения среди х1, …,xn, то 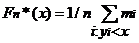 .
.
Эмпирическая функция распределения Fn *(х) служит статистическим аналогом (оценкой) неизвестной функции распределения F (x), которую называют при этом теоретической. Если х1, …, xn – выборка объема n из генеральной совокупности, имеющей непрерывное распределение с неизвестной плотностью вероятностей f x(x)= f (x), то для получения статистического аналога f (х) следует произвести группировку данных. Она состоит в следующем:
1. По данной выборке х1, …, xn строят вариационный ряд x (1) £x (2) £…£x ( n ).
2. Промежуток [ x (1), x ( n )] разбивают точками u0 = х (1), u1, …, uL = x(n): u0 < u1 <…< uL на L непересекающихся интервалов Jk = [ uk–1, uk) (на практике L << n).
3. Подсчитывают частоты νk попадания выборочных значений в k -ый интервал Jk.
4. Полученную информацию заносят в таблицу, которую называют интервальным статистическим рядом (таблица 3).
Таблица 3 – Интервальный статистический ряд
| Интервалы Jk | [ u0, u1) | [ u1, u2) | … | [ uL–1, uL ] |
| Частоты νk | ν1 | ν2 | … | νL |
Относительные частоты 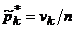
| n1 / n | ν2 / n | … | nL / n |
Очевидно, что 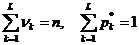 . Поэтому совокупность пар
. Поэтому совокупность пар
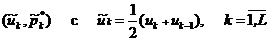
называют иногда эмпирическим законом распределения, полученным по сгруппированным данным. Далее в прямоугольной системе координат на каждом интервале Jk как на основании длины ∆ uk = uk – uk-1 строят прямоугольник с высотой 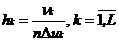 . Получаемую при этом ступенчатую фигуру называют гистограммой. Поскольку при больших n выполняется
. Получаемую при этом ступенчатую фигуру называют гистограммой. Поскольку при больших n выполняется 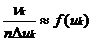 , то верхнюю границу гистограммы можно рассматривать как оценку неизвестной плотности f (x).
, то верхнюю границу гистограммы можно рассматривать как оценку неизвестной плотности f (x).
Ломаная с вершинами в точках 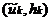 называется полигоном частот и для гладких плотностей является более точной оценкой, чем гистограмма.
называется полигоном частот и для гладких плотностей является более точной оценкой, чем гистограмма.
На практике при группировке данных обычно берут интервалы одинаковой длины ∆ u =соnst, а число интервалов группировки определяют с помощью так называемого правила Стаджерса, согласно которому полагается
L = [1+3,32 ln(n)]+1,
или следующими рекомендациями:
при n≥1000 L=11…15;
n≥400 L=10;
n≥200 L=9;
100<n<200 критерий применяют в исключительных случаях с числом интервалов L=7…9.
Если интервалы выбраны одинаковой длины, то ширина их равна 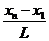 .
.
Располагая только сгруппированными данными, можно определить аналог эмпирической функции распределения следующим образом:
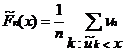 .
.
Статистическим аналогом (оценкой) теоретической числовой характеристики
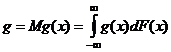 .
.
является выборочная (эмпирическая) числовая характеристика g *, определяемая как среднее арифметическое значений функции g (х) для элементов выборки х1, …, xn:
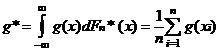 .
.
В частности, k -й выборочный момент есть величина
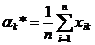 .
.
При k = 1 величину α * 1 называют выборочным средним и обозначают 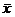 :
:
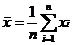 .
.
При k =2 величину μ2 * называют выборочной дисперсией и обозначают s 2:
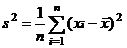 .
.
Между выборочными начальными и выборочными центральными моментами сохраняются те же соотношения, что и между теоретическими. Например, справедливо равенство
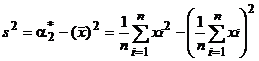 ,
,
являющееся аналогом известного равенства μ2 = DX = α 2– α12 = М{X} 2–(М{X})2. Для вычисления выборочных моментов k -го порядка по сгруппированным данным используются формулы:
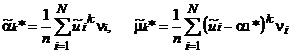 .
.
В частности, выборочное среднее и выборочная дисперсия по сгруппированным данным определяются с помощью формул
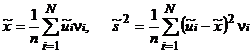 .
.
Date: 2015-07-17; view: 2050; Нарушение авторских прав