Моделирование нормального распределения

Наиболее часто встречающимся видом распределения является нормальное. В связи с этим при моделировании различных явлений возникает потребность иметь в распределении последовательности случайных чисел, отвечающих нормальному закону распределения. Реализация случайной величины с нормальным распределением N(0;1) с помощью классических методов продемонстрирована выше на примере аппроксимации функции (3). Кроме этих методов, разработаны специальные методы, позволяющие получать с большой скоростью достаточно длинные последовательности случайных чисел, отвечающих нормальному закону распределения. На первом этапе выполняют реализацию случайной величины с плотностью N(0;1). При помощи линейного преобразования

y_i=μ+σx_i, i=1, 2, …, (18)

при любом μ и σ > 0 можно затем получить последовательность случайных чисел y₁, y₂, …, отвечающих распределению N (μ; σ²) с математическим ожиданием M(Y)=μ и дисперсией D(Y)= σ².

Один из самых известных методов реализации нормально распределенной случайной величины при использовании ЭВМ основан на центральной предельной теореме, в соответствии с которой распределение суммы независимых случайных величин X_i(i=1, 2, …, n) приближается к нормальному при неограниченном увеличении n, если выполняются следующие условия:

а) все величины имеют конечные математические ожидания и дисперсии;

б) ни одна из величин по своему значению резко не отличается от всех остальных.

Согласно этой теореме можно сконструировать алгоритм реализации случайной величины X на основе аппроксимации распределения N(0;1) суммой независимых случайных величин R₁, R₂, …, R_n, равномерно распределенных на интервале [0;1). Практика показывает, что при n=12 аппроксимация уже довольно удовлетворительна. В результате получаем формулу для вычисления нормально распределенной случайной величины

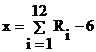. (19)

В другом известном генераторе нормально распределенных случайных величин используется точный обратный метод Бокса и Малера, который дает хорошие результаты, легко программируется и достаточно быстро работает. По этому методу генерируется пара нормированных нормальных чисел (μ=0, σ=1) из двух стандартных случайных чисел (R₁ и R₂ на интервале от 0 до 1) с помощью следующих уравнений:

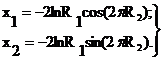(20)

Модификацией этого метода является процедура Марсальи и Брея, в соответствии с которой генерируются два случайных числа R₁ и R₂. Далее, полагая V₁ = -1+2R₁ и V₂ = -1+2R₂, вычисляют S= 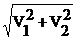. При S≥1 начинают цикл снова. При S<1 реализуют отбор, т.е.

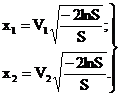(21)

Date: 2015-07-17; view: 1796; Нарушение авторских прав