Проверка гипотезы о виде распределения

Пусть х₁, …, x_n – выборка объема n, представляющая собой результат n независимых наблюдений над случайной величиной X, относительно распределения которой выдвинута простая гипотеза Н₀: F_X (х) = F (х). (F (х) – теоретическая функция распределения, соответствующая гипотезе Н₀).

Наиболее распространенным критерием проверки этой гипотезы Н₀ является критерии c² Пирсона. Чтобы воспользоваться критерием c² Пирсона, выборочные данные х₁, …,x_n следует предварительно сгруппировать, представив их в виде интервального статистического ряда (см. таблицу 3).

Пусть 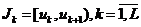– интервалы группировки; n ₁,…,n _L – частоты попадания выборочных значений в интервалы J₁,..., J_L соответственно (n₁ +... + n_L = n). Обозначим р_k теоретическую (соответствующую Н₀) вероятность попадания случайной величины Х в интервал 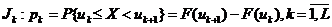, где F(u_k+1), F(u_k) – значение теоретической функции распределения соответственно на правой и левой границах k-ого интервала гистограммы, построенной по таблице 3.

При расчетах принимают F(u₁)=0, F(u_L+1)=1.

Статистикой критерия c² является величина ,

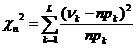где L – количество интервалов гистограммы, построенной по таблице 3;

ν_k – количество реализаций СВ, попавших в k-й интервал;

p_k – вероятность попадания случайной величины в k-й интервал, вычисленная для теоретического закона распределения;

n – объем выборки (количество случайных чисел в выборке).

Она характеризует отклонение эмпирической функции распределения F_n *(х) (n _k / n – приращение F_n *(х) на интервале J_k) от теоретической функции распределения F (х) (р_k – приращение F (х) на том же интервале J_k). Поскольку относительные частоты n _k / n сближаются с вероятностями р_k при n ®¥, 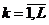, то в случае справедливости Н₀ значение величины c _n ² не должно существенно отличаться от нуля. Поэтому критическая область критерия c² задается в виде К_a ={ t ³ t_a }, где t = c _n ²(х₁, …,x_n) – значение величины c _n ², вычисленное для заданной выборки, а порог t_a определяется по заданному уровню значимости a так, чтобы Р {c _n ²Î K_a / H₀ }=a. Нахождение t_a основано на том факте (известном как теорема Пирсона), что случайная величина c _n ² имеет при n ®¥ предельное распределение хи-квадрат с (L- 1) степенью свободы c²(L- 1).

На практике предельное распределение c²(L -1) можно использовать с хорошим приближением при n ³50 и n_k ³5, 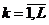. При выполнении этих условий для заданного уровня значимости a можно положить t_a =c²_1-a,L-1, где c²_{1-a, L -1}– (1-a)-квантиль распределения c²(L -1).

Таким образом, критерий согласия c² Пирсона состоит в следующем:

1. По таблице 3 строят интервальный статистический ряд.

2. Строится гистограмма.

3. По виду гистограммы формулируется гипотеза о виде закона распределения.

4. Вычисляются теоретические вероятности попадания случайной величины в каждый из интервалов гистограммы по формуле .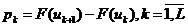

5. Вычисляется значение статистики c² _n (х₁, …,x_n)= t.

6. По таблице распределения для вычисленного значения c² _n и числа степеней свободы n=s=L-k-1, где k – количество параметров теоретического закона распределения (для экспоненциального равно 1, для нормального и Вейбулла – 2), по заданному уровню значимости s находится по табл. П4 порог c²_{1-a, L-1}.

7. Если t ³c²_{1-a, L -1}, то гипотезу Н₀ отвергают.

8. Если t <c²_{1-a, L -1}, то гипотезу Н₀ принимают.

Если случайная величина X дискретная, х_k, 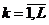– различные выборочные значения, а Р { Х = х_k }= р_k в случае справедливости Н₀, то всегда можно определить L интервалов, содержащих ровно по одному выборочному значению. Поэтому в данном случае можно сразу считать, что n_k = m_k, 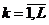, где m_k – частота выборочного значения х_k.

Date: 2015-07-17; view: 689; Нарушение авторских прав