Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Комбинация метода суперпозиций и метода отбора
|
|
Выражение (10) позволяет реализовать комбинированный метод, если каждую из плотностей fi=(x) представить в виде:
fi(x)=aiωi(x)gi(x) (11)
где ai – постоянные (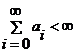
),
ωi(x) – некоторые известные плотности вероятностей,
gi(x) – функция, которая для каждого x удовлетворяет условию 0≤gi(x)≤1.
В результате для получения последовательности случайных чисел может быть использован следующий алгоритм:
а) реализация случайной величины Y по дискретному распределению p(Y=i)=pi, i=0, 1, 2, …;
б) реализация случайной величины X по плотности вероятности ωi(x) c параметром i, полученным в пункте (a). Эта часть алгоритма совпадает с методом суперпозиций. Затем следует использование метода отбора на основе представления плотности fi(x) в виде формулы (11);
в) реализация случайной величины R, равномерно распределенной на интервале [0; 1);
г) если R<gi(x), то считаем, что полученное в пункте (б) значение является одним из значений случайной величины X с плотностью f(x). В противном случае повторяем все вычисления, начиная с пункта (a).
Комбинация метода суперпозиций и метода отбора позволяет реализовать случайную величину практически с любым законом распределения.
Пример 8. Рассмотрим способ генерирования случайных чисел с нормальным законом распределения N(0;1), основанный на аппроксимации (3). Представим f(x) в виде следующей суммы:
f(x)=p1ω1(x)g1(x)+p2ω2(x)g2(x). (12)
Пусть
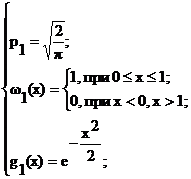
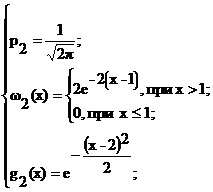
Для выполнения в (12) условия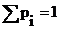 
пронормируем p1 и p2. Вследствие этого в пункте (a) алгоритма реализация случайной величины Y будет выполняться с вероятностью р1/(p1 + p2)=2/3 по плотности ω1(x). Причем при R>g1(Y) полученное значение случайной величины Y будет отбрасываться. С вероятностью р2/(p1 + p2)=1/3 реализация случайной величины Y будет выполняться по плотности ω2(x). Исключению будут подвергаться те выработанные числа, которые удовлетворяют условию R>g2(Y). Реализуя случайную величину S, принимающую значения “+1” и “-1” с вероятностями 0.5, и вычисляя S·X, получают в итоге случайные числа, распределенные по N(0;1), -∞<x<∞.
Date: 2015-07-17; view: 1153; Нарушение авторских прав