Проверка статистических гипотез

Статистической гипотезой называют любое утверждение о виде или свойствах наблюдаемых в эксперименте случайных величин. Правило, позволяющее по имеющимся статистическим данным (выборке) принять или отклонить выдвинутую гипотезу, называется статистическим критерием.

Если формулируется только одна гипотеза Н₀ и требуется проверить, согласуются ли статистические данные с этой гипотезой или же они ее опровергают, то критерии, используемые для этого, называются критериями согласия.

Если гипотеза Н₀ однозначно фиксирует закон распределения наблюдаемых случайных величии, то она называется простой, в противном случае – сложной.

Пусть относительно наблюдаемой случайной величины Х сформулирована некоторая гипотеза Н₀; х₁, …,x_n – выборка объема n, являющаяся реализацией случайного вектора (X₁,..., Х_n), координаты которого X_i, 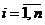независимы и распределены так же, как X.

Общий метод построения критерия согласия для проверки гипотезы Н₀ состоит в следующем. Вначале ищут статистику Т = Т (Х₁,..., Х_n) (случайную величину!), характеризующую отклонение эмпирического распределения от теоретического, распределение которой в случае справедливости Н₀ можно определить (точно или приближенно). Далее задают некоторое положительное малое число a, так что событие с вероятностью a можно считать практически невозможным в данном эксперименте. Затем для заданного a определяют подмножество K_a в множестве К = { t: t = Т (х₁,…,x_n)} возможных значений статистики Т, так чтобы Р { Т { Х₁,..., X_n)Î K_a / H₀ }£a. Критерий согласия имеет следующий вид:

- если t = Т(х₁, …, x_n) – значение статистики T (Х₁,..., X_n), соответствующее данной выборке х₁, … x_n и t Î K_a, то гипотеза Н₀ отвергается;

- если t Ï K_a, то гипотеза Н₀ принимается.

Статистика Т = Т (Х₁,..., Х_n) называется статистикой критерия; множество К_a – критической областью для гипотезы Н₀, число a–уровнем значимости критерия.

Date: 2015-07-17; view: 791; Нарушение авторских прав