Метод отбора

Данный метод предложен Дж. Нейманом и сущность его сводится к тому, что из области задания случайной величины X “отбирается” точка с координатами, являющимися фикциями случайных чисел с равномерным распределением; если эта точка не может быть использована для расчета X, происходит ее “отбрасывание” и “отбирается” новая. Метод отбора применим для получения реализаций только таких случайных величин, закон распределения которых может быть задан с помощью функции плотности.

В рамках метода отбора существует несколько процедур моделирования случайной величины с заданной плотностью распределения.

2.2.1 Метод отбора – процедура № 1

С помощью данной процедуры моделируется одномерная случайная величина X, определенная на интервале плотностью f(x). Вне этого интервала f(x)=0 и, кроме того, плотность распределения ограничена сверху, т.е. f(x)≤С, где С – постоянная.

Процедура № 1 получения значений случайной величины графически показана на рисунке 4 и заключается в следующем:

а) получаем два независимых значения r₁ и r₂ случайной величины R с равномерным распределением на интервале [0; 1);

б) строим точку с координатами (z₁, z₂), где z₁=a+r₁(b-a); z₂=r₂c;

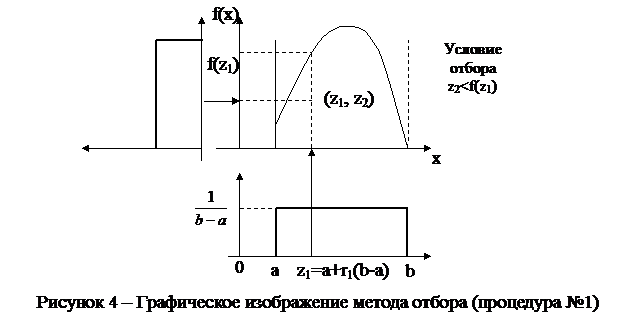
в) если z₂<f(z₁), то полагаем, что случайная величина X приняла значение z₁;

если z₂ ≥ f(z₁), то точка z=(z₁, z₂) отбрасывается, и вычисления повторяются с получением новой пары случайных чисел (r_n, r_n+1) по пункту а.

Эффективностью метода отбора называют вероятность того, что точка z=(z₁, z₂) будет использована для расчета X. В рассмотренной процедуре № 1 эффективность метода характеризуется отношением площади, ограниченной кривой f(x), осью x, прямыми x=a и x=b, к площади прямоугольника C(b-a).

2.2.2 Метод отбора – процедура № 2

Пусть случайная величина X имеет распределение с плотностью f(x), которую можно представить в виде

f(x)=a₁f₁(x)g₁(x), (6)

где a₁ – постоянная;

f(x) – некоторая известная плотность вероятности, а функция g₁(x) удовлетворяет условию 0≤g₁(x)≤1.

Значения случайной величины Х можно получить по следующему алгоритму (см. рисунок 5):

а) моделируем случайную величину Y с плотностью распределения f₁(x);

б) вычисляем g₁(Y);

в) моделируем случайную величину R, равномерно распределенную на интервале [0; 1);

г) если R< g₁(Y), то принимаем x=Y. В противном случае полученные числа отклоняются и вычисления повторяются с пункта (а).

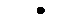2.2.3 Метод отбора – процедура № 3

Если в (6) функция g₁(x) является монотонно неубывающей, то получается следующий алгоритм:

а) моделируем случайную величину Y с плотностью f₁(x);

б) моделируем случайную величину γ с функцией распределения g₁(γ);

в) если γ<Υ, то принимаем x=Y, в противном случае полученные числа отклоняем и вычисления повторяем с пункта (а).

2.2.4 Метод отбора – процедура № 4

Процедура № 4 определяет процесс моделирования случайной величины X, если плотность f(x) можно представить в виде

f(x)=a₁(1-g₁(x))f₁(x), (7)

где g₁(x)= g(t(x)), причем g₁ - монотонно неубывающая функция, а g - некоторая известная функция распределения.

Значения случайной величины X тогда можно получить по следующему алгоритму:

а) моделируем случайную величину Y с плотностью распределения f₁(x);

б) вычисляем величину t(Y);

в) моделируем случайную величину γ с функцией распределения g;

г) если γ>t(Y), то принимаем x=Y. В противном случае полученные числа отклоняются и повторяются вычисления с пункта (а).

Пример 6. Для усеченного нормального распределения (x>0) и с учетом аппроксимации (3) можно плотность распределения представить в виде

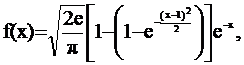(8)

Введя обозначения:

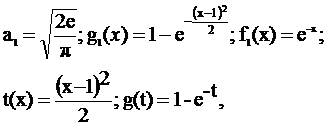
можно убедиться в выполнении разложения f(x) в виде (7).

Date: 2015-07-17; view: 2386; Нарушение авторских прав