Метод обратных функций

Лабораторная работа № 2

Моделирование случайных чисел с заданным законом распределения

Цель работы

Изучение методов и получение навыков составления алгоритмов генерации псевдослучайных чисел с различными законами распределения, наиболее часто используемых при имитационном моделировании сложных систем на ЭВМ.

Методические указания

В процессе анализа и проектирования имитационных моделей стохастических систем возникает необходимость задания различных случайных воздействий или имитирования стохастических процессов. Подобные ситуации предопределяют необходимость программной генерации случайных чисел с некоторым законом распределения. Пусть требуется получить (смоделировать) реализацию случайной величины X с плотностью распределения f(x). Данная задача решается путем моделирования случайной величины R, равномерно распределенной на интервале [0;1), и преобразования последовательности случайных чисел r₁, r₂, …, r_n в последовательность x₁, x₂, …, x_n. В общем случае преобразование можно реализовать с помощью некоторой функции

X=ψ(R), (1)

связывающей случайные числа с равномерным распределением со случайными числами с заданным законом распределения. Преобразование (1) может быть выполнено различными методами.

Метод обратных функций

Пусть требуется получить значения случайной величины X, распределенной в интервале (a;b) с плотностью вероятности f(x).

Стандартный метод моделирования основан на том, что интегральная функция распределения 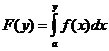любой непрерывной случайной величины равномерно распределена в интервале (0;1), т.е. для любой случайной величины X с плотностью распределения f(x) случайная величина равномерно распределена на интервале (0;1).

Тогда случайную величину X с произвольной плотностью распределения f(x) можно рассчитать по следующему алгоритму, графическое решение смотрите на рисунке 1:

1. Необходимо сгенерировать случайную величину r (значение случайной величины R), равномерно распределенную в интервале (0;1).

2. Приравнять сгенерированное случайное число известной функции распределения F( X ) и получить уравнение .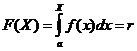

3. Решая уравнение X=F^-1(r), находим искомое значение X.

Такой способ получения случайных величин называется методом обратных функций.

Пример 1. Пусть требуется получить случайную величину X, распределенную в интервале (a; b) с равномерной плотностью:

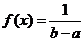, a<x<b.

Тогда F(x)= 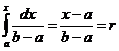и получаем следующее выражение: x=a+r∙(b-a). Эта формула часто используется для расширения или смещения стандартного интервала (0;1) равномерно распределенной случайной величины до необходимого интервала (a; b).

Следует отметить, что не всегда возможно так легко разрешить получаемые уравнения. Чаще всего аналитическое решение не существует, и тогда приходится прибегать к численному решению уравнения x=F^-1(r).

Так выглядит пример теоретически, практически же:

Пример 2. Разыграть 3 возможных значения непрерывной случайной величины X, распределенной равномерно в интервале (2; 10).

Решение:

Функция распределения величины X имеет следующий вид:

F(x)=(x-a)/(b-a).

По условию, a = 2, b = 10, следовательно, F(x)=(x-2)/8.

В соответствии с алгоритмом разыгрывания непрерывной случайной величины приравняем F(x) выбранному случайному числу r_i. Получим отсюда:

(x_i - 2) / 8 = r_i => x_i = 8r_i + 2

Далее в соответствии с алгоритмом выберем три случайных числа, распределенных равномерно в интервале (0;1). Например, r₁ = 0,11; r₂ = 0,17; r₃ = 0,66.0

Подставим эти числа в уравнение. Получим соответствующие возможные значения X:

x₁=8∙0,11+2=2,88; x₂=8∙0,17+2=3,36; x₃=8∙0,66+2=7,28.

Пример 3. Показательное распределение. Метод логарифма [1].

Случайная величина X имеет экспоненциальный (показательный) закон распределения

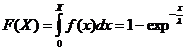, x≥0, λ>0;

где λ – параметр распределения.

Очевидно, если r=F(x)= 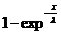, то X=F^-1(r)=-λln(1-r).

Так как 1-r имеет то же самое распределение, что и R, то удобнее при нахождении значений случайной величины X пользоваться формулой

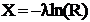. (2)

Случай, когда R=0, должен трактоваться особо; его можно заменять любым подходящим значением exp, так как вероятность возникновения этого случая крайне мала.

Пример 4. Обратную функцию для нормального распределения нельзя представить в виде простых, легко вычисляемых формул. Поэтому для получения случайных чисел с нормальным распределением используют аппроксимацию:

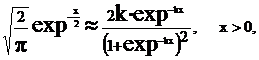(3)

где .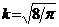

Если воспользоваться (3) для случайной величины с плотностью

, -¥<x<¥,

то получим для положительной полуоси методом обратных функций величину

(4)

Если значениям x, полученным с помощью (4), приписывать с вероятностью 0,5 знак “+” и с вероятностью 0,5 знак “-”, то полученная последовательность случайных чисел может рассматриваться как реализация случайных величин S·X с нормальным распределением N (0;1), -∞<x<∞, где S – случайная величина с распределением

Пример 5. Метод обратного преобразования можно также использовать, если величина X является дискретной. В этом случае функция распределения

,

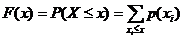где p(x_i) – является вероятностной мерой p(x_i)=P(X=x_i). (Допускается, что величина X может иметь только такие значения x₁, x₂, …, для которых x₁< x₂<….) Тогда алгоритм будет иметь следующий вид.

1. Генерируем число R в интервале (0;1).

2. Определяем положительное наименьшее целое число R_i, для которого R_i≤F(x_i), и возвращаем X=x_i.

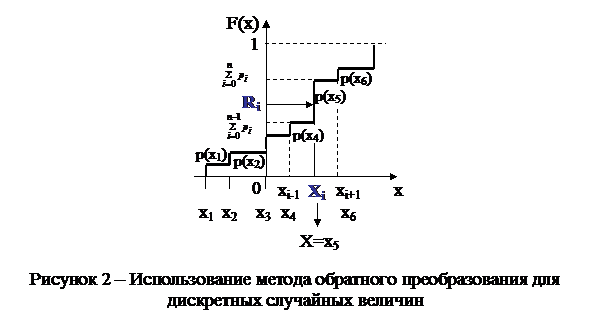
Метод обратного преобразования для непрерывных и дискретных величин можно, формально, объединить в одну общую формулу

X=min{x: F(x)≥R} (5)

Графически формула (5) представлена на рисунке 2.

Таким образом, если явного выражения для обратной функции получить не удается, то используются приближенные способы моделирования случайных величин. Они основаны на аппроксимации функции F(х) некоторой другой функцией G(х), обратная функция которой G^-1 имеет более простое аналитическое выражение и легко вычислима.

Н.П. Бусленко предложен метод кусочно-линейной аппроксимации, при котором функция распределения F(х) заменяется функцией F*(х), составленной из отрезков прямых. Для этого интеграл изменения функции F(х) разбивается на n подынтервалов, число которых зависит от требуемой точности конечных результатов. На каждом из линейных участков F*(х), соответствующих этим подынтервалам, определяется обратная функция. При этом функция распределения на выделенных подынтервалах может быть аппроксимирована не только линейной, но и другой подходящей простой функцией, если требуется более высокая степень точности результатов моделирования.

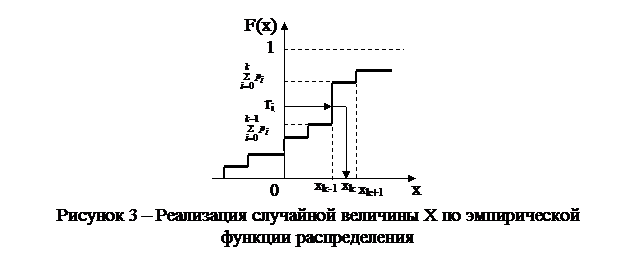
Метод обратных функций применяется также при моделировании случайной величины X по эмпирической функции ее распределения, построенной по результатам выборки. На рисунке 3 показана реализация случайной величины X по эмпирической функции распределения, являющейся ступенчатой ломаной линией. Случайные числа (реализации случайной величины Х) принимаются равными (x_k-1+x_k)/2, т.е. они соответствуют серединам интервалов (x_k-1; x_k) если случайная величина R попадает в интервал .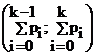

Date: 2015-07-17; view: 18272; Нарушение авторских прав