По какому критерию и как проверяется равенство дисперсий нескольких выборок одинакового объёма?

При проверки гипотезы о равенстве дисперсий предполагают, что сравниваемые генеральные совокупности X и Y распределены по нормальному закону. По независимым выборкам объемами n₁ и n₂, извлечённым из этих совокупностей, определены статистические оценки дисперсий и по формулам (3.1) - (3.2):

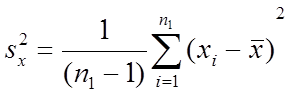, (3.1)

(3.2)

По этим дисперсиям при заданном уровне значимости α требуется проверить нулевую гипотезу, состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой: Н₀: D[X]=D[Y]. Если окажется, что нулевая гипотеза справедлива, т.е. генеральные дисперсии равны, то различие статистических оценок дисперсий незначимо и объясняется случайными причинами, в частности случайным отбором объектов выборки. Например, если различие вычисленных дисперсий результатов измерений, выполненных двумя приборами, оказалось незначимым, то приборы имеют одинаковую точность. Иначе говоря, для имеющихся данных различие в точности приборов не обнаружено, (относительный принцип«верифицируемости», см. главу 1). И наоборот, если нулевая гипотеза будет отвергнута, то различие статистических оценок дисперсий значимо и не может быть объяснено случайными причинами, т.е. делается вывод, что, например, точность методов контроля или контрольных приборов различна. Этот результат уже не может подвергаться сомнению (абсолютный принцип«фальсифицируемости», см. главу 1).

Критическая область строится в зависимости от вида конкурирующей гипотезы; при этом рассматривают два случая.

1. Конкурирующая гипотеза о превышении первой дисперсии H₁: D[X]>D[Y] (односторонняя гипотеза).

Вычисляется наблюдаемое значение критерия (отношение большей дисперсии к меньшей):

(3.3)

Традиционно по таблице критических точек распределения Фишера по заданному уровню значимости α и числам степеней свободы k₁ = n₁ - - l, k₂ = n₂ -1 (k₁ - число степеней свободы большей дисперсии) определяют критическую точку F_кр (α, k₁, k₂).

Если F_B < F_кр, то нет оснований отвергнуть нулевую гипотезу. Если F_B > F_кр, нулевую гипотезу отвергают, т. е. делается вывод: первая дисперсия существенно больше второй.

2. Конкурирующая гипотеза H₁: D[X] ≠ D[Y].

В отличие от предыдущей односторонней гипотезы в данном случае критическую точку F_кр(α/2, k₁, k₂) определяют по уровню значимости α/2 (так как критическая область двусторонняя). Если F_B < F_КР, то нет оснований отвергать нулевую гипотезу. Если F_B > F_КР, нулевую гипотезу отвергают, т. е. делается вывод: дисперсии не равны.

Для измерения значимости рассматриваемого критерия (например, F_B) при отклонении нулевой гипотезы H₀ используется «вероятность значимости» P(F≤f), которая определяет вероятность принадлежности критерия множеству области значимости в предположении, что верна нулевая гипотеза H₀. Результаты опытов согласуются с нулевой гипотезой H₀, когда «вероятность значимости» велика, и не согласуются, когда «вероятность значимости» мала. То есть чем меньше значение «вероятности значимости» P(F≤ f), тем более это свидетельствует против гипотезы H₀. Вероятность значимости для первого случая проверки гипотезы (одностороннего) определяется как , а для второго (двустороннего) случая проверки гипотезы - как .

15. Опишите, какие инструменты статистического анализа и какие статистические функции программы MS Excel используются для проверки статистической гипотезы о равенстве:

- дисперсий двух выборок;

- средних значений двух выборок с известными дисперсиями;

- средних значений двух выборок с неизвестными дисперсиями;

- среднего значения выборки известной величине;

Date: 2016-08-31; view: 692; Нарушение авторских прав