
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Что означают понятия «вариационный ряд», «статистический ряд», «интервальный статистический ряд», «гистограмма», «полигон частот»?
|
|
Назовите требования к точечным оценкам; объясните их сущность и приведите примеры.
Точечная оценка - числовая характеристика положения математического ожидания или степени и характера дисперсности рассеяния случайной величины. (Математическое ожидание, МО - это то значение случайной величины, к которому стремится её среднее значение с увеличением n.)
Требования к точечным оценкам. Для того чтобы оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям: должны быть несмещёнными, эффективными и состоятельными.
Несмещённая оценка в среднем совпадает с истинным значением оцениваемого параметра.
Эффективная оценка характеризуется минимальной дисперсией в сравнении со всеми другими несмещёнными оценками.
Состоятельная оценка с ростом объёма выборки приближается к истинному значению оцениваемого параметра.
Целесообразно разделить точечные оценки на оценки, так или иначе характеризующие положение рассеяния на числовой оси, и оценки, характеризующие степень и характер рассеяния случайной величины.
Что означают понятия «вариационный ряд», «статистический ряд», «интервальный статистический ряд», «гистограмма», «полигон частот»?
Одним из самых простых представлений статистических данных является их упорядочение по величине. Пусть (х1,..., хn) - выборка объемаn из генеральной совокупности X. Ее можно упорядочить, расположив значения в неубывающем порядке, образуя «вариационный ряд»:
x(1) ≤ x(2) ≤…≤ x(i)≤… ≤ x(n), (1.1)
где x(1)- наименьший, x(n)- наибольший из элементов выборки.
x(i)(иногда обозначают Z(i))соответственно - члены вариационного ряда.
Распределение случайной величины подчиняется определённым законам, может, например, концентрироваться в центре интервала шкалы или наоборот, рассеиваться равномерно в пределах некоего интервала. От распределения случайной величины зависит способ обращения с ней, способ её оценки.
Наиболее простой характеристикой распределения и одновременно способом упорядочения и способом представления случайной величины является статистический ряд. Это таблица, которая в первой строке содержит значения Z(i), а во второй - числа их повторений (табл. 1.1). Число ni называют частотой, а отношение ni/n - относительной частотой.
Таблица 1.1.Статистический ряд
| Z(1) | Z(2) | … | Z(m) |
| n1 | n2 | … | nm |
Статистические данные,представленные в виде статистического ряда, называют группированными.
Разновидностьстатистического ряда - интервальный статистический ряд ( таблица 1.2). В интервальном статистическом ряде исходные данные группируют следующим образом: отрезок J, содержащий все выборочные значения, разбивают на mпромежутков Ji,как правило, одинаковой длины. При этом считают, что каждый промежуток содержит своё левое граничное значение, но лишь последний промежуток содержит и своё правое граничное значение.
Таблица 1.2.Интервальный статистический ряд
| J1 | J2 | … | Jm | J |
| n1 | n2 | … | nm | 
|
Иногда в верхней строке табл. 1.2 указывают не интервал, а его середину, а в нижней строке вместо частоты записывают относительную частоту ni/n. Число промежутков m, на которые разбивают отрезок J, выбирают в зависимости от объема выборки n. Для ориентировочной оценки величины mможно пользоваться формулой:
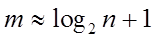 (1.2)
(1.2)
Статистический или интервальный ряд можно представить графиком, называемым гистограммой (рис. 1.1), составленным из прямоугольников с высотами ni или ni/n. Нетрудно увидеть, что в последнем случае суммарная площадь всех прямоугольников, образующих такую диаграмму, равна 1:
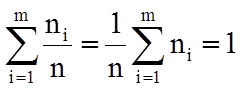 (1.3)
(1.3)
Эмпирическое распределение случайной величины X, представленное выборкой объёмом n, можно изобразить графиком, называемым гистограммой (рис. 1.1), полученной на основе статистического ряда или интервального статистического ряда [27]. Он состоит из прямоугольников, построенных на интервалах (отрезках числовой оси), как правило, одинаковой длины, высотой, равной абсолютной (ni) или относительной (ni/n) частоте попадания X в соответствующие интервалы.
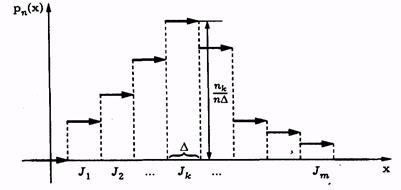
Рис.1.1.Гистограмма случайной величины X
Наряду с гистограммой для описания плотности рассеяния случайной величины X часто используют другое графическое представление, называемое полигоном частот. Это ломаная линия, отрезки которой соединяют середины горизонтальных верхних сторон прямоугольников в гистограмме (рис. 1.2).

Рис. 1.2. Гистограмма (пунктир) и полигон частот эмпирическойфункциираспределения
5 .Нарисуйте график плотности стандартного нормального распределения, указав на нём величины среднего значения и стандартного отклонения. В чём его «удобство» по сравнению с «обычным» нормальным распределением? Какие ещё распределения случайных величин Вы знаете?
По виду гистограммы или полигона частот можно судить о характере плотности рассеяния случайной величины X. Например, по распределениям, представленным на рис. 1.1 и 1.2, видно, что плотность распределения максимальна в середине рассматриваемого интервала шкалы x и минимальна по краям.
Эмпирической плотностью распределения называют функцию, которая во всех точках области распределения Jпринимает значение относительных частот, а вне области Jравна нулю.
Для непрерывных случайных величин, анализу которых посвящено настоящее учебное пособие, длина интервалов Jk (см. рис. 1.1 и 1.2) может быть бесконечно малой. Тогда график плотности распределения из гистограммы или полигона частот преобразуется в непрерывную функцию плотности непрерывного распределения, рис. 1.3.

Рис. 1.3. Графики плотности распределения дискретной и непрерывной случайных величин (D - наибольшее возможное значение дискретной величины d, Xmin, Xmax - пределы, за которыми f(x)=0
То есть характеристика плотности распределения непрерывной случайной величины X f(x) является статистическим аналогом плотности распределения дискретной случайной величины P(d) = ni/n.
Для определения вероятности попадания дискретных или непрерывных случайных величин в заданный интервал шкалы X производится соответственно суммирование или интегрирование плотности P(d) или f(x) на этом интервале (см. рис. 1.3).
Интегральной (накопленной) функцией распределенияназывают дискретную  или непрерывную функцию
или непрерывную функцию 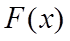 =
= 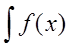 . Фактически функция F(x), задаёт для любого значения х вероятность того, что случайная величина X меньше или равна х: F(x) = P(X< x)
. Фактически функция F(x), задаёт для любого значения х вероятность того, что случайная величина X меньше или равна х: F(x) = P(X< x)
Как и функции плотности (см. рис. 1.3), графики интегральных функций дискретного и непрерывного распределения приведены в сравнении на рис. 1.4. Видно, что максимальное значение интегральной функции F(x) = 1, что выражает 100 % площади фигуры, находящейся под кривой графика плотности распределения (см. рис. 1.3).

Рис. 1.4. Графики интегральных функций дискретного и непрерывного
распределения
С целью наглядного представления роли и взаимодействия плотности и интегральных функций на рис. 1.5 для произвольного непрерывного распределения изображены совместно графики плотности f(x) (вверху) и соответствующей интегральной функции F(x) (внизу). Здесь x1 и x2 - границы рассматриваемого интервала какого-либо параметра X, например, размера детали. Тогда по графику f(x) можно судить о частоте попадания параметра X в интервал x1 - x2: наглядно видно, что с большей вероятностью параметр X попадает приблизительно в середину интервала, а с меньшей вероятностью - по краям, особенно с левого края. Суммарная вероятность попадания параметра X в интервал x1 - x2 выражается заштрихованной площадью на графике f(x), см. рис. 1.5. Но она также равна разности значений интегральной функции F(x2) - F(x1), см. нижнюю часть рис. 1.5.
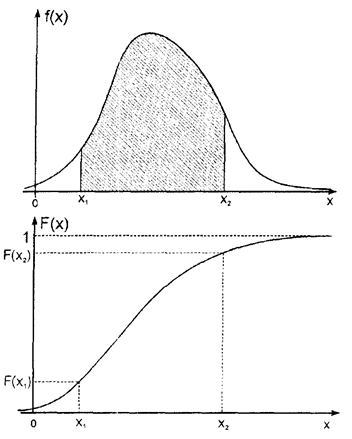
Рис. 1.5. Плотность f(x) и соответствующая интегральная функция F(x) произвольного распределения непрерывной случайной величины
Назовите основные точечные оценки положения рассеяния случайных величин на числовой оси и приведите известные Вам формулы их определения: аналитические и используемые в рамках программы MS Excel.
Наиболее употребляемые показатели положения рассеяния на числовой оси достаточно условно разбиты на отдельные подгруппы (рис. 2.1).

Рис. 2.1. Характеристики положения
Ниже указаны наиболее важные оценки положения.
Выборочное среднее (среднее арифметическое, математическое ожидание) случайной величины  обозначается как
обозначается как 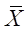 , удовлетворяет всем приведённым выше требованиям к точечным оценкам. Ниже приведена формула (2.1) оценки
, удовлетворяет всем приведённым выше требованиям к точечным оценкам. Ниже приведена формула (2.1) оценки 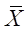 для случая, когда значения
для случая, когда значения  разбиты по интервалам:
разбиты по интервалам:
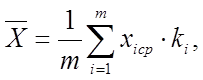 (2.1)
(2.1)
где  - среднее значение
- среднее значение 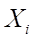 в i-м интервале,
в i-м интервале,
ki - количество значений 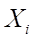 , попадающих в i-й интервал.
, попадающих в i-й интервал.
Медиана (Me) x1/2, квартили х1/4, х1/2, х3/4, децили х0,1...х0,9 (или х01...х09 ) и процентили х0,01...х0,99 (или х001...х099 ) делят область изменения Х соответственно на 2, 4, 10 или 100 интервалов.
Мода (Мо) случайной величины - наиболее вероятное значение случайной величины. Иначе - это значение случайной величины, при котором плотность распределения вероятностей имеет максимум.
Квантиль среди показателей положения рассеяния на числовой оси имеетособое значение (см. рис. 2.2), т.к. он непосредственно определяется интегральной функцией распределения случайной величины. Квантиль (хγ) порядка γ распределения вероятностей (0 < γ < 1) есть такое значение хγ случайной величины X, для которого функция распределения принимает значение γ.

Рис. 2.2. Квантиль случайной величины X
Date: 2016-08-31; view: 529; Нарушение авторских прав