Назовите основные точечные оценки степени рассеяния случайных величин и приведите известные Вам формулы их определения: аналитические и используемые в рамках программы MS Excel.

Характеристики рассеяния относительно центра классифицируются на показатели трёх типов: «кучности» разброса, асимметрии и определяемые законом распределения (рис. 2.3).

Рис. 2.3. Характеристики степени и характера рассеяния

Ниже рассмотрены наиболее важные из них.

Выборочная дисперсия - среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .

(2.2)

Для генеральной совокупности оценка дисперсии по формуле (2.2) удовлетворяет всем требованиям, предъявляемым к точечным оценкам (см. выше), но применительно к выборке она является смещённой оценкой генеральной дисперсии. Для исправления выборочной дисперсии достаточно умножить ее на дробь Поэтому в качестве исправленной несмещённой оценки генеральной дисперсии по выборке, особенно если n относительно невелико (n < 30), обычно используют:

(2.3)

где - среднее значение выборки.

Если все значения случайной величины сгруппированы по k интервалам, где имеют частоты n₁, n₂,… n_j,…, n_k, то формула (2.3) принимает вид:

(2.4)

Стандартное (среднее квадратичное) отклонение (СКО) в отличие от дисперсии имеет размерность, равную размерности . Для выборки (S) и генеральной совокупности () оно определяется соответственно:

(2.5)

Замечания:

1. Выборочное СКО S является лишь оценкой СКО генеральной совокупности σ. Поэтому в отличие от σ определяется с некоторой погрешностью, которая в свою очередь определяется как СКО величины выборочного СКО S_S, рассчитываемой по формуле:

(2.6)

Видно, что погрешность оценки уменьшается пропорционально увеличению квадратного корня из объёма выборки n, то есть стремится к 0 при бесконечном увеличении n.

2. С целью повышения точности (уменьшения S и S_S), например, в случае измерении какого-то параметра, этот замер повторяют несколько (n) раз, а потом усредняют. Тогда средняя квадратическая ошибка среднего значения 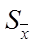уменьшается относительно СКО единичного значения x_i 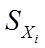, вычисляемого по формулам (2.3-2.5), пропорционально квадратному корню из количества n произведённых измерений:

, (2.7)

3. Большинство характеристик (кроме асимметрии и эксцесса, подробно описанных в §2.1.4, см. также рис. 2.3) имеют одну особенность - наличие размерности, что не даёт возможности объективно сравнивать разброс величин, имеющих разную размерность. Таким недостатком не обладает коэффициент вариации (V), представляющий собой отношение выборочного СКО к среднему (или при n → ∞ СКО к МО):

, (2.8)

4. Из формул (2.7) и (2.8) определяется показатель точности среднего значения , иначе «коэффициент вариации для среднего»:

. (2.9)

5. Приведённые выше формулы универсальны, применимы для выборок, состоящих из самых различных величин. Но в ряде случаев перед проведением описанных расчётов характеристик рассеяния бывает полезна операция приведения к единичному стандартному отклонению. Для этого приводят значения x_i к среднему значению:

x_{пi =} x_{i -} . Затем, умножая преобразованные значения x_пi на 1/s, получают преобразованную выборку случайной величины Z: которая имеет нулевое выборочное среднее значе­ние и равное единице выборочное СКО.

8. Расскажите, как и с использованием каких статистических функций программы MS Excel по известной выборке можно быстро и просто определить:

Date: 2016-08-31; view: 489; Нарушение авторских прав